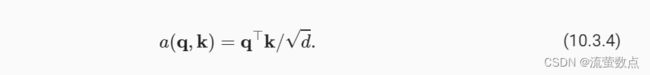注意力评分函数（掩蔽softmax操作，加性注意力,缩放点积注意力）

• 将注意力汇聚的输出计算可以作为值的加权平均，选择不同的注意力评分函数会带来不同的注意力汇聚操作。

• 当查询和键是不同长度的矢量时，可以使用可加性注意力评分函数。当它们的长度相同时，使用缩放的“点－积”注意力评分函数的计算效率更高。

注意力汇聚：Nadaraya-Watson 核回归_流萤数点的博客-CSDN博客使用了高斯核来对查询和键之间的关系建模。 (10.2.6)中的 高斯核指数部分可以视为注意力评分函数（attention scoring function）， 简称评分函数（scoring function）， 然后把这个函数的输出结果输入到softmax函数中进行运算。 通过上述步骤，将得到与键对应的值的概率分布（即注意力权重）。 最后，注意力汇聚的输出就是基于这些注意力权重的值的加权和。

从宏观来看，上述算法可以用来实现 图10.1.3中的注意力机制框架。

 图10.3.1说明了 如何将注意力汇聚的输出计算成为值的加权和， 其中a表示注意力评分函数。 由于注意力权重是概率分布， 因此加权和其本质上是加权平均值。

正如上图所示，选择不同的注意力评分函数a会导致不同的注意力汇聚操作。 本节将介绍两个流行的评分函数，稍后将用他们来实现更复杂的注意力机制。

pip install mxnet==1.7.0.post1

pip install d2l==0.15.0

import math
from mxnet import np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l

npx.set_np()

1.掩蔽softmax操作

正如上面提到的，softmax操作用于输出一个概率分布作为注意力权重。 在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。 例如，为了在 9.5节中高效处理小批量数据集， 某些文本序列被填充了没有意义的特殊词元。 为了仅将有意义的词元作为值来获取注意力汇聚， 可以指定一个有效序列长度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。 下面的masked_softmax函数 实现了这样的掩蔽softmax操作（masked softmax operation）， 其中任何超出有效长度的位置都被掩蔽并置为0。

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return npx.softmax(X)
    else:
        shape = X.shape
        if valid_lens.ndim == 1:
            valid_lens = valid_lens.repeat(shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = npx.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, True,
                              value=-1e6, axis=1)
        return npx.softmax(X).reshape(shape)

为了演示此函数是如何工作的， 考虑由两个2×4矩阵表示的样本， 这两个样本的有效长度分别为2和3。 经过掩蔽softmax操作，超出有效长度的值都被掩蔽为0。

masked_softmax(np.random.uniform(size=(2, 2, 4)), np.array([2, 3]))

array([[[0.488994  , 0.511006  , 0.        , 0.        ],
        [0.4365484 , 0.56345165, 0.        , 0.        ]],

       [[0.288171  , 0.3519408 , 0.3598882 , 0.        ],
        [0.29034296, 0.25239873, 0.45725837, 0.        ]]])

同样，也可以使用二维张量，为矩阵样本中的每一行指定有效长度。

masked_softmax(np.random.uniform(size=(2, 2, 4)),
               np.array([[1, 3], [2, 4]]))

array([[[1.        , 0.        , 0.        , 0.        ],
        [0.35848376, 0.3658879 , 0.27562833, 0.        ]],

       [[0.54370314, 0.45629686, 0.        , 0.        ],
        [0.19598778, 0.25580427, 0.19916739, 0.3490406 ]]])

 

2.加性注意力

 下面来实现加性注意力。

#@save
class AdditiveAttention(nn.Block):
    """加性注意力"""
    def __init__(self, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        # 使用'flatten=False'只转换最后一个轴，以便其他轴的形状保持不变
        self.W_k = nn.Dense(num_hiddens, use_bias=False, flatten=False)
        self.W_q = nn.Dense(num_hiddens, use_bias=False, flatten=False)
        self.w_v = nn.Dense(1, use_bias=False, flatten=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播的方式进行求和
        features = np.expand_dims(queries, axis=2) + np.expand_dims(
            keys, axis=1)
        features = np.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = np.squeeze(self.w_v(features), axis=-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return npx.batch_dot(self.dropout(self.attention_weights), values)

用一个小例子来演示上面的AdditiveAttention类， 其中查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小）， 实际输出为(2,1,20)、(2,10,2)和(2,10,4)。 注意力汇聚输出的形状为（批量大小，查询的步数，值的维度）。

queries, keys = np.random.normal(0, 1, (2, 1, 20)), np.ones((2, 10, 2))
# values的小批量数据集中，两个值矩阵是相同的
values = np.arange(40).reshape(1, 10, 4).repeat(2, axis=0)
valid_lens = np.array([2, 6])

attention = AdditiveAttention(num_hiddens=8, dropout=0.1)
attention.initialize()
attention(queries, keys, values, valid_lens)

array([[[ 2.      ,  3.      ,  4.      ,  5.      ]],

       [[10.      , 11.      , 12.000001, 13.      ]]])

 

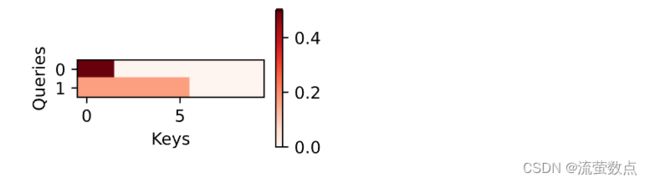
尽管加性注意力包含了可学习的参数，但由于本例子中每个键都是相同的， 所以注意力权重是均匀的，由指定的有效长度决定。

#@save
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),
                  cmap='Reds'):
    """显示矩阵热图"""
    d2l.use_svg_display()
    num_rows, num_cols = matrices.shape[0], matrices.shape[1]
    fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,
                                 sharex=True, sharey=True, squeeze=False)
    for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):
        for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):
            pcm = ax.imshow(matrix.asnumpy(), cmap=cmap)
            if i == num_rows - 1:
                ax.set_xlabel(xlabel)
            if j == 0:
                ax.set_ylabel(ylabel)
            if titles:
                ax.set_title(titles[j])
    fig.colorbar(pcm, ax=axes, shrink=0.6);

show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

 

 

3.缩放点积注意力

使用点积可以得到计算效率更高的评分函数， 但是点积操作要求查询和键具有相同的长度d。 假设查询和键的所有元素都是独立的随机变量， 并且都满足零均值和单位方差， 那么两个向量的点积的均值为0，方差为d。 为确保无论向量长度如何， 点积的方差在不考虑向量长度的情况下仍然是1， 我们再将点积除以， 则缩放点积注意力（scaled dot-product attention）评分函数为：

下面的缩放点积注意力的实现使用了暂退法进行模型正则化。

#@save
class DotProductAttention(nn.Block):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = npx.batch_dot(queries, keys, transpose_b=True) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return npx.batch_dot(self.dropout(self.attention_weights), values)

 为了演示上述的DotProductAttention类， 我们使用与先前加性注意力例子中相同的键、值和有效长度。 对于点积操作，我们令查询的特征维度与键的特征维度大小相同。

queries = np.random.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.initialize()
attention(queries, keys, values, valid_lens)

array([[[ 2.      ,  3.      ,  4.      ,  5.      ]],

       [[10.      , 11.      , 12.000001, 13.      ]]])

 

与加性注意力演示相同，由于键包含的是相同的元素， 而这些元素无法通过任何查询进行区分，因此获得了均匀的注意力权重。

show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')