C++ 树进阶系列之线段树和它的延迟更新

1. 前言

线段树和树状数组有相似之处，可以用于解决区间类型的问题。

但两者又各个千秋，树状数组本质是数组，有着树的形，可以借用树的一些概念。线段树是典型的二叉树结构，无论神和形都是树，可以应用树的所有理论。

本文将详细聊聊线段树。

2. 问题驱动

与树状数组一样，线段树可以缓存区间内具有特殊性质的数据（如：区间和，区间最值、…），以提高操作性能。

现通过一个案例理解线段树的初衷。

如有如下数组，现有求任意区间内最大值的需求。最简单的解决方案是使用穷举法求最值，时间复杂度O(n)。

如果求某个区间中的最值是一个高频率操作，每次都使用穷举法计算，累积的时间代价是非常大的。

在代码中，当需要对相同的计算频繁调用时，首当其冲的想法必然是缓存机制。针对本题可以使用简单动态规划思想，缓存原数组中每一个位置的最大值。

#include 
using namespace std;
int main() {
	//原数组
	int nums[8]= {3,6,1,9,7,11,8,5};
	//最大值缓存数组
	int cache[8]= {0};
	cout<<"原数组中数据"<

输出结果：

缓存时间复杂度是O(n)，求最值时间复杂度为O(1)，如果原数组中的数据是稳定的，不失为一种良好的方案。

但是，如果原数组中的数据有频繁更新需求时，则需要随时联动更新整个缓存数组，时间性能会变得较大。

线段树的基本思路和树状数组一样，仅对区间信息缓存，更新也仅针对区间进行，线段树的时间复杂度为O(logn)。

3. 线段树的构建流程

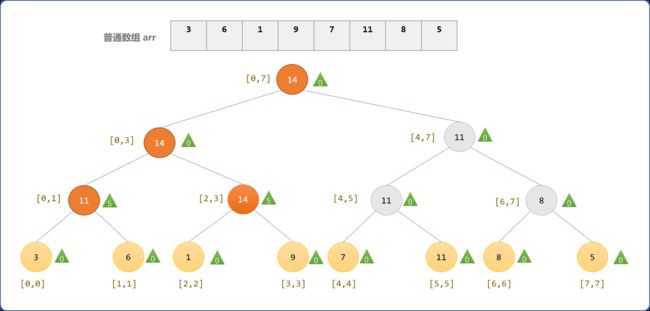
在探讨线段树的构建之前，先看一下最终线段树的形状。

分析结果图可知：

• 原数组arr中的每一个数据都是线段树的叶结点。
• 非叶结点的值是在其左、右子结点的值中选择了较大哪个。
• 结点至少包含 3 个信息(值或称权重，左、右边界值)。且叶结点的区间特征是左、右边界值相同。
• 整个数组就是一个大区间，区间边界从0到7，可统一描述格式为[0,7]。

根据分析，构建的基本思路：

• 父结点向左、右子结点发送请求，获取左、右子结点上的值。
• 如果左、右子结点不是叶结点，则继续向自己的左、右子结点发送值的请求。
• 如果左、右子结点是叶结点，则把值回送给父结点。
• 父结点获取到左、右子结点值后，求两者中的最大值作为自己的值。

上面的过程显然符合递归的向后请求、向上回溯的执行模式。下面根据原数组提供的信息，使用递归思想构建出完整的线段树。

• 构建根结点，区间信息为 [0,7]，值未知。

• 构建根结点的左、右子结点。对根结点的区间[0,7]使用二分思想，划分成左、右 2 个子区间，左区间范围[0,7/2]，右区间范围[7/2+1,7]，此时，左、右子结点点值任然未知。

• 以此类推，继续对非叶结点的区间信息采用二分思想，以子区间信息构建子结点。

• 直到区间不能再分（左、右边界相同），此时构建出来的结点是叶结点。以叶结点的区间值为索引号，从原数组中获取值。

• 然后把值向父结点提供，父结点会选择较大的值作为自己的值。

• 一路向上，直到根结点的值被填充。

最终可以看到构建出了一个满二叉树。

是不是对于任意一个数列中的数据都能构建出满二叉树？

不一定，只能说是一棵近似的完全二叉树。

因本例中数组恰好有 8 个数据。

根据二叉树的原理。树的深度为logn+1，n=8时，深度h=4。

而又知，二叉树的最后一层的结点数最多为 2^h-1，把h=4代入后可知值为8。当最后一层达到最大数量时，此二叉树方为满二叉树。如果原数组中的数据只有 5 或其它个数，最后一层是不可能达到满二叉树所要的数量。

4. 线段树的 API

原数组中的数据个数不同，所构建出来的线段树不一定是满二叉树，或者说一定是完全二叉树，但也是一棵近似完全二叉树。因为完全二叉树中父结点和子结点的存在如下的位置关系。

• 如果父结点的位置为 i。
• 如果存在左、右子结点，则左子结点的位置为 i*2、右子结点的位置为 2*i+1。
• 如果已知子结点的位置i，则父结点的位置是 i/2。根结点的父结点位置为 0。

有了这个良好的数学关系，线段树常使用数组方式进行存储。

4.1 结点类

结点类中有一个lazy属性，称为延迟更新值，延迟更新是线段树的一个显著的特点。暂且不表，在线段树的区间更新时再深聊。

#include 
#include 
using namespace std;
struct TreeNode {
	//编号,与结点存储位置对应
	int code;
	//结点的值（权重）
	int value;
	//左边界
	int left;
	//右边界
	int right;
	//延迟更新值
	int lazy; 
	/*
	*无参构造 
	*/
	TreeNode() {
		this->code=0;
		this->lazy=0;
	}
	/*
	*有参构造 
	*/ 
	TreeNode(int code,int value,int left,int right) {
		this->code=code;
		this->value=value;
		this->left=left;
		this->right=right;
		this->lazy=0;
	}
	/*
	*自我显示 
	*/ 
	void desc() {
		cout<<"结点存储位置："<code<<"，区间：["<left<<","<right<<"]，值："<value<

4.2 线段树类

class SegmentTree {
	private:
		//使用数组存储线段树的结点
		TreeNode** st;
         //线段树大小
		int size;
	public:
		SegmentTree(int size):size(size) {
			//树的深度
			int h=ceil(log2(size)) +1;
             //数组的大小
			this->size=pow(2,h);
			this->st=new TreeNode*[this->size] {NULL};
		}
		/*
		* 初始化线段树
		* arr: 原数组
		* pos: 线段树中的位置
		* left：左区间
		* right：右区间
		*/
		int initTree(int* arr,int pos, int left,int right);
		/*
		* 查找指定区间的最大值
		*/
		int getMax(int left,int right);
		/*
		*单点更新
		*/
		int update(int pos,int index,int val);
		/*
		*区间更新
		*/
		int queryUpdate(int pos,int left,int right,int val);
        /*
        *显示树结点
        */
		void showAll() {
			for(int i=0; isize; i++) {
				if(this->st[i]!=NULL)
					this->st[i]->desc();
			}
		}
};

4.2.1 初始化函数

使用递归初始化整个线段树。

int SegmentTree::initTree(int* arr,int pos, int left,int right) {
	if(left==right) {
		//如果左、右边界相同
		this->st[pos]=new TreeNode(pos,arr[left],left,right);
        //叶结点是递归出口
		return arr[left];
	}
    //二分思想划分左右区间
	int mid=(right+left)/2;
	//初始左子结点 
	int lVal= initTree(arr,2*pos,left,mid);
	//初始右子结点
	int rVal= initTree(arr,2*pos+1,mid+1,right);
	//找左、右子结点中的较大值
	int val=max(lVal,rVal);
	//以较大值创建结点
	this->st[pos]=new TreeNode(pos,val,left,right);
	return val;
}

测试构建线段树：

4.2.2 区间查询

查询指定区间中的最大值，需分几种情况讨论。

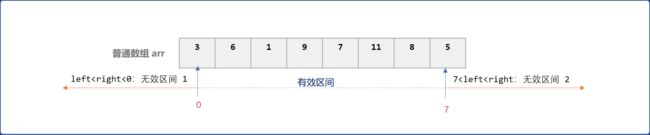
• 无效区间。如下图所示，[left,right]中的left>7或right<0时。返回无解。

• 完整包含。当[left,right]中的left<=0 and right>=7时。返回[0,7]区间的最大值。

• 匹配左或右子区间。查找左、或右子空间中的最大值。
  

• 与左、右子空间相集。为左、右子空间中较大的值，即为[0,7]区间最大值。

/*
*区间查找
*/
int SegmentTree::getMax(int left,int right) {
    //从根结点开始查找
    int pos=1;
    //移动指针
    TreeNode* move=NULL;
    while(1) {
        move=this->st[pos];
        if (left>move->right || rightleft )
            //无效区间
            return 1>>31;
        else if( left<=move->left && right>=move->right )
            //查找区间恰好包含在此区间
            return move->value;
        else {
            //中间位置
            int mid=(move->left+move->right)/2;
            if( right<=mid )
                //左边查找
                pos=move->code*2;
            else if(left>=mid )
                //右边查找
                pos=move->code*2+1;
            else
                return move->value;
        }
    }
}

测试区间查找：

int main() {
	//省略……
	int res= segmentTree.getMax(2,7);
	cout<<"区间[2,7]最大值："<

输出结果：

4.2.3 单点更新

单点更新某一个叶结点上的值。使用递归方案一路向下查询到叶结点，再在回溯过程中更新非叶结点。和初始线段树的逻辑相似。

/*
*单点更新
*/
int update(int pos,int index,int val) {
    TreeNode* move=this->st[pos];
    if( move->left== move->right ) {
        //如果是叶结点，直接更新
        this->st[pos]->value+=val;
        return 	this->st[pos]->value;
    }
    //不是叶结点
    int mid= (move->left+move->right)/2;
    int lVal=0;
    int rVal=0;
    int mx=0;
    if( index<=mid ) {
        //更新左边子区间
        lVal=update(pos*2,index,val);
        //在更新后的左子区间和右子区间中找出较大的值
        mx=max(lVal,this->st[pos*2+1]->value );
    } else {
        //更新右子空间
        rVal=update(pos*2+1,index,val);
        //在更新后的右子区间和左子区间中找出较大的值
        mx=max(this->st[pos*2]->value, rVal);
    }
    //更新当前位置
    this->st[pos]->value=mx;
    return mx;
}

测试单点更新：

int main() {
    //省略……
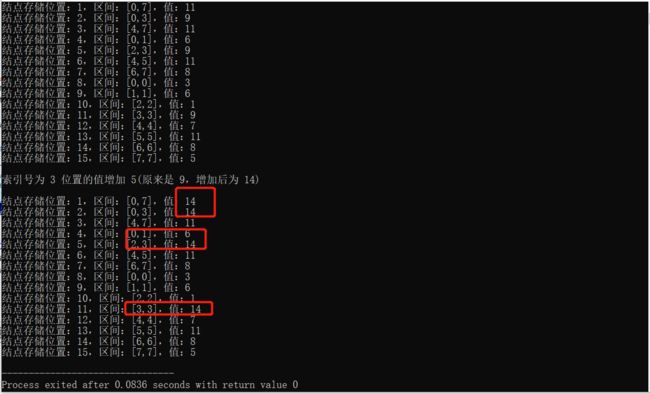
   cout<<"\n索引号为 3 位置的值增加 5(原来是 9，增加后为 14) \n"<

输出结果：

当同时需要更新的叶结点较多时，因为单点更新的时间复杂度为O(logn)，如果逐次调用单点更新函数，需要能达到最终结点，时间复杂度为O(n*logn)。

线段树提供了延迟更新策略，算是线段树最高光之处。

4.2.4 区间更新

区间更新并不要求一步到位，而是利用了积累的力量。基本思想是边查询边更新，查询到哪里更新到哪里。

如下图所示，线段树上的每一个结点都有一个lazy延迟更新属性，初始值为 0。

• 当需要让[0,3]区间内所有叶结点值+5时。更新会延迟到当某次需要查询[0,3]区间的最大值时，这时从根结点向下查询到[0,3]结点9。让结点 9的值增加为 14，且结点 9 的 lazy属性存储增量5后再把 14 返回给根结点，让根结点更新为14。

• 当下次需要查询[0,1]区间内最大值时。当查询到[0,3]且发现其lazy属性值不等于0。则会把此值向左、右子结点传递。

/*
*区间更新
*/
int SegmentTree::queryUpdate(int pos,int left,int right,int val) {
    //移动指针
    TreeNode* move=this->st[pos];
    if (left>move->right || rightleft )
        //无效区间
        return 1>>31;
    if( left<=move->left && right>=move->right ) {
        //查找区间恰好包含在此区间
        move->lazy+=val;
        move->value+=move->lazy;
        //叶结点，清除延迟值
        move->lazy=move->left==move->right?0:move->lazy;
        return move->value;
    }
    //中间位置
    int mid=(move->left+move->right)/2;
    int lVal=0;
    int rVal=0;
    int mx=0;
    if(move->lazy!=0) {
        //延迟值向左、右子结点传递
        this->st[pos*2]->lazy=move->lazy;
        this->st[pos*2+1]->lazy=move->lazy;
        //清零
        move->lazy=0;
    }
    if(right<=mid ) {
        //查询左边
        lVal= queryUpdate(pos*2,left,right,val);
        this->st[pos]->value=max(move->value, lVal);
        return lVal;
    } else if(left>=mid ) {
        //右边查找
        rVal=queryUpdate(pos*2+1,left,right,val);
        this->st[pos]->value=max(move->value, rVal);
        return rVal;
    } else {
        //查找区间恰好包含在此区间
        move->lazy+=val;
        move->value+=move->lazy;
        //叶结点，清除延迟值
        move->lazy=move->left==move->right?0:move->lazy;
        return move->value;
    }
}

测试区间更新：

int main() {
	//省略……
	cout<<"\n对区间[0,3]的结点值加 5，查询时更新： \n"<

输出结果： 可以看到[，当查询到[0,0]结点时，些结点才一次性全部更新。

5. 总结

线段树是很有个性的数据结构，常用于解决区间类型问题。线段树有一个延迟更新理念，通过查询深度不同，更新到的深度也不一样。