机器学习-神经网络

神经网络是有具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

---

M-P神经元

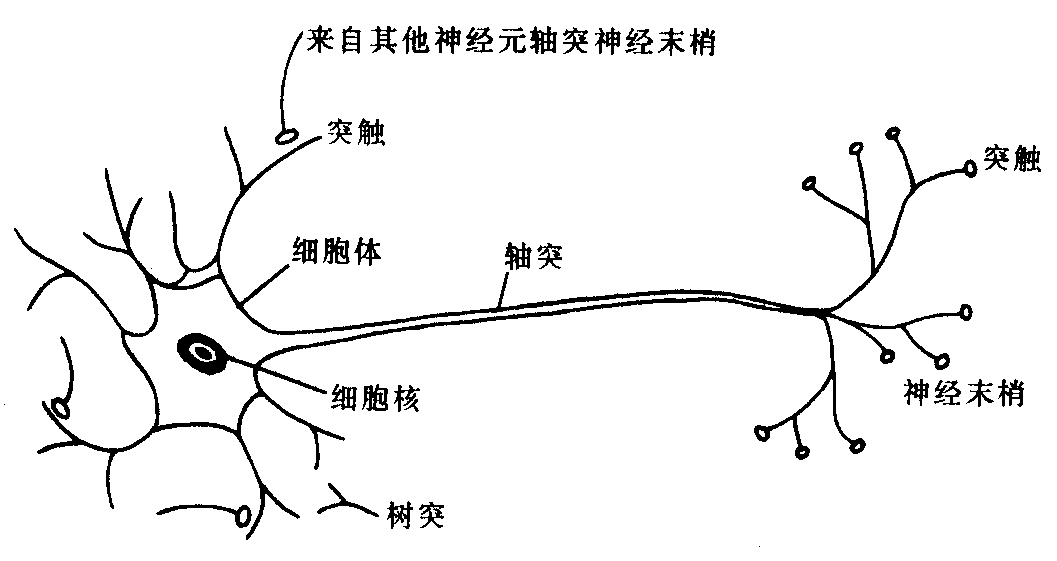
      生物中的生物神经元：

      神经网络中最基本的成分是神经元模型，即“简单单元”。在M-P神经网络模型中，神经元接收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过“激活函数”处理以产生神经元的输出。

      *10个神经元两两连接，则有100个参数，90个连接权和10个阈值。

---

激活函数

理想中的激活是阶跃函数，它将输入值映射为输出值0和1，显然1对应于神经元兴奋，0对应于神经元抑制。然而，阶跃函数具有不连续、不光滑等不太好的性质，因此实际常用Sigmoid函数作为激活函数。对数几率函数则是Sigmoid函数的典型代表。因函数将较大范围的输入值挤压到(0,1)输出值范围内，因此有时也称为“挤压函数”。

---

感知机

      感知机是由两层神经元组成，输入层接受外界输入信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”。

      给定训练数据集，权重wi以及阈值可通过学习得到。阈值可以看作一个固定输入为-1.0的“哑结点”所对应的连接权重，这样，权重和阈值的学习就可统一为权重的学习。

      感知机学习规则非常简单，对训练样例(x，y)，若当前感知机的输出为，则感知机权重进行如下调整：

      △

      △

      其中称为学习率。若感知机对训练样例(x，y)预测正确，即y=，则感知机不发生变化，否则将根据错误的程度进行权重调整。

      感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力非常有限。与、或、非问题都是线性可分的问题，感知机可以很容易实现其逻辑运算。若两类模式是线性可分的，即存在一个线性超平面能将它们分开，则感知机的学习过程一定会收敛而求得适当的权向量w=（,,...,）。否则感知机学习过程将会发生振荡，权向量难以稳定下来，不能求得合适解，例如感知机不能解决异或这样的简单的非线性可分问题。

      使用两层感知机解决异或问题：

---

多层网络

      要解决非线性问题，需考虑使用多层功能神经元。如可使用两层感知机解决异或问题。输出层和输入层之间的一层神经元，被称为隐层或隐含层，隐含层和输出层都是拥有激活函数的功能神经元。

      常见的神经网络有着丰富的层级结构，每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层链接。这样的神经网络结构通常称为“多层前馈神经网络”，其中输入层神经元接受外界输入，隐层和输出层神经元对信号进行加工，最终结果有输出层神经元输出。换言之，输出层神经元仅是接受输入，不进行函数处理，隐层和输出层包含功能神经元。

      *前馈并不意味着网络中信号不能向后传，而是指网络拓扑结构上不存在环或回路。

      神经网络的学习过程，就是根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值。换言之，神经网络“学”到的东西，蕴含在连接权与阈值中。

---

反向传播算法BP算法

      多层网络的学习能力比单层感知机强的多，同样其需要更强大的学习算法。BP算法即反向传播算法，又称误差传播算法，是目前最常用的神经网络学习算法。常说的BP网络就是指使用BP算法的多层前馈神经网络。

      BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整。学习率控制着算法每一轮迭代中的更新步长，若太大则容易振荡，太小则收敛速度又会过慢。

      BP算法工作流程：

      1.先将输入示例提供给输入神经元，逐层将信号前传，直到产生输出层的结果。

      2.计算输出层的误差，并将误差逆向传播至隐层神经元。

      3.最后根据隐层神经元的误差来对连接权和阈值进行调整。

      该迭代过程循环进行，直到达到某些停止条件为止。

---

标准BP和累积BP

      标准BP算法每次仅针对一个训练样例更新连接权和阈值。累积BP算法针对累积误差最小化进行更新。

      一般来说，标准BP算法每次更新只能针对单个样例，参数更新得非常频繁，而且不同样例进行更新的效果可能出现“抵消”现象。因此，为了达到同样的累积误差极小点，标准BP算法往往需进行更多次数的迭代。

      累积BP算法直接针对累积误差最小化，它在读取整个训练集D一遍后(one epoch)才对参数进行更新，其参数更新的频率低得多。

      在很多任务中，累积误差下降到一定程度后，进一步下降会非常缓慢，这时标准BP往往会更快获得较好的解，尤其是在训练集D非常大时更明显。

---

过拟合处理

      BP神经网络经常遭遇过拟合，其训练误差持续降低，但测试误差却可能上升。有两种策略常用来缓解BP网络的过拟合：

      1.早停

      将数据分为训练集和验证集，训练集用来计算梯度、更新连接权和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。

      2.正则化

      基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如连接权与阈值的平方和。增加连接权和阈值平方和这一项后，训练过程将会偏好较小的连接权和阈值，使网络输出更加“光滑”，从而对过拟合有所缓解。

---

局部极小和全局最小

      参数空间内梯度为零的点，只要其误差函数值小于邻点的误差函数值，就是局部极小点。可能存在多个局部极小值，但却只会有一个全局最小值。也就是说“全局最小”一定是局部极小，反之则不成立。

      基于梯度的搜索是使用最为广泛的参数寻优方法。在此类方法中，从某些初始值出发，迭代寻找最优参数值。每次迭代中，先计算误差函数在当前点的梯度，然后根据梯度确定搜索方向。由于负梯度方向是函数值下降最快的方向，因此梯度下降法就是沿着负梯度方向搜索最优解。若误差函数在当前点的梯度为零，则已达到局部极小，更新量将为零，这意味着参数的迭代更新将在此停止。显然，如果误差函数仅有一个局部极小，那么此时找到的局部极小就是全局最小。然而如果函数具有多个局部极小，则不能保证找到的解是全局最小。对于这一情形，称为参数寻优陷入了局部极小。

      跳出局部极小，启发式技术主要有以下几种：

      1.以多组不同参数初始化多个神经网络，按标准方法训练后，取其中误差最小的解作为最终参数。这相当于从多个不同的初始点开始搜索，这样就可能陷入不同的局部极小，从中进行选择有可能获得更接近全局最小的结果。

      2.使用“模拟退火”技术。模拟退火在每一步都以一定概率接受比当前解更差的结果，从而有助于跳出局部极小。在每次迭代过程中，接受次优解的概率要随着时间的推移而逐渐降低，从而保证算法稳定。

      3.使用随机梯度下降。与标准梯度下降法精确计算梯度不同，随机梯度下降法在计算梯度时加入了随机因素。于是，即便陷入局部极小点，它计算出的梯度仍可能不为零，这样就有机会跳出局部极小继续搜索。

      4.遗传算法