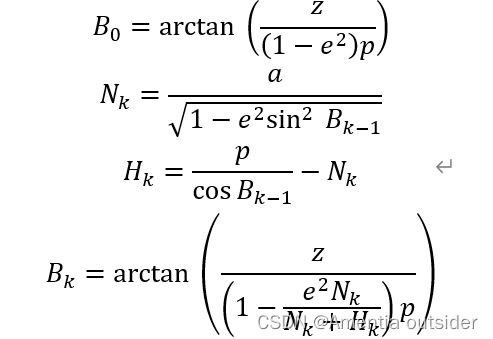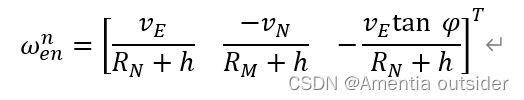GNSS-INS组合导航：KF-GINS（二）

Earth.h文件

基于Eigen库矩阵计算。

1、WGS84确定椭球模型参数

const double WGS84_WIE = 7.2921151467E-5;       /* 地球自转角速度*/
const double WGS84_F   = 0.0033528106647474805; /* 扁率 */
const double WGS84_RA  = 6378137.0000000000;    /* 长半轴a */
const double WGS84_RB  = 6356752.3142451793;    /* 短半轴b */
const double WGS84_GM0 = 398600441800000.00;    /* 地球引力常数 */
const double WGS84_E1  = 0.0066943799901413156; /* 第一偏心率平方 */
const double WGS84_E2  = 0.0067394967422764341; /* 第二偏心率平方 */

2、计算重力

class Earth {

public:
    /* 正常重力计算 */
    static double gravity(const Vector3d &blh) {

        double sin2 = sin(blh[0]);
        sin2 *= sin2;

        return 9.7803267715 * (1 + 0.0052790414 * sin2 + 0.0000232718 * sin2 * sin2) +
               blh[2] * (0.0000000043977311 * sin2 - 0.0000030876910891) + 0.0000000000007211 * blh[2] * blh[2];
    }

与严老师PSINS中的代码相近

eth.g = eth.g0*(1+5.27094e-3*eth.sl2+2.32718e-5*sl4)-3.086e-6*pos(3); % grs80

 3、计算子午圈半径

 /* 计算子午圈半径和卯酉圈半径 */
    static Eigen::Vector2d meridianPrimeVerticalRadius(double lat) {
        double tmp, sqrttmp;

        tmp = sin(lat);
        tmp *= tmp;
        tmp     = 1 - WGS84_E1 * tmp;
        sqrttmp = sqrt(tmp);

        return {WGS84_RA * (1 - WGS84_E1) / (sqrttmp * tmp), WGS84_RA / sqrttmp};
    }

4、计算卯酉圈半径

 static double RN(double lat) {
        double sinlat = sin(lat);
        return WGS84_RA / sqrt(1.0 - WGS84_E1 * sinlat * sinlat);
    }

 

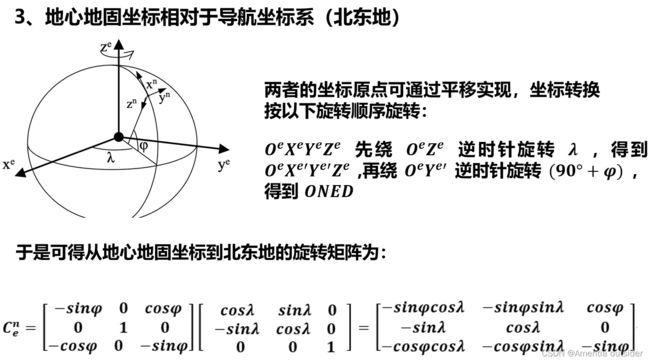
5、n系到e系转换矩阵

static Matrix3d cne(const Vector3d &blh) {
        double coslon, sinlon, coslat, sinlat;

        sinlat = sin(blh[0]);
        sinlon = sin(blh[1]);
        coslat = cos(blh[0]);
        coslon = cos(blh[1]);

        Matrix3d dcm;
        dcm(0, 0) = -sinlat * coslon;
        dcm(0, 1) = -sinlon;
        dcm(0, 2) = -coslat * coslon;

        dcm(1, 0) = -sinlat * sinlon;
        dcm(1, 1) = coslon;
        dcm(1, 2) = -coslat * sinlon;

        dcm(2, 0) = coslat;
        dcm(2, 1) = 0;
        dcm(2, 2) = -sinlat;

        return dcm;
    }

 6、n系到e系转换四元数

static Quaterniond qne(const Vector3d &blh) {
        Quaterniond quat;

        double coslon, sinlon, coslat, sinlat;

        coslon = cos(blh[1] * 0.5);
        sinlon = sin(blh[1] * 0.5);
        coslat = cos(-M_PI * 0.25 - blh[0] * 0.5);
        sinlat = sin(-M_PI * 0.25 - blh[0] * 0.5);

        quat.w() = coslat * coslon;
        quat.x() = -sinlat * sinlon;
        quat.y() = sinlat * coslon;
        quat.z() = coslat * sinlon;

        return quat;
    }

 7、从n系到e系转换四元数得到经纬度

static Vector3d blh(const Quaterniond &qne, double height) {
        return {-2 * atan(qne.y() / qne.w()) - M_PI * 0.5, 2 * atan2(qne.z(), qne.w()), height};
    }

8、地理坐标转地心地固坐标

 /* 大地坐标(纬度、经度和高程)转地心地固坐标 */
    static Vector3d blh2ecef(const Vector3d &blh) {
        double coslat, sinlat, coslon, sinlon;
        double rnh, rn;

        coslat = cos(blh[0]);
        sinlat = sin(blh[0]);
        coslon = cos(blh[1]);
        sinlon = sin(blh[1]);

        rn  = RN(blh[0]);
        rnh = rn + blh[2];

        return {rnh * coslat * coslon, rnh * coslat * sinlon, (rnh - rn * WGS84_E1) * sinlat};
    }

 9、地心地固坐标系转地理坐标

tatic Vector3d ecef2blh(const Vector3d &ecef) {
        double p = sqrt(ecef[0] * ecef[0] + ecef[1] * ecef[1]);
        double rn;
        double lat, lon;
        double h = 0, h2;

        // 初始状态
        lat = atan(ecef[2] / (p * (1.0 - WGS84_E1)));
        lon = 2.0 * atan2(ecef[1], ecef[0] + p);

        do {
            h2  = h;
            rn  = RN(lat);
            h   = p / cos(lat) - rn;
            lat = atan(ecef[2] / (p * (1.0 - WGS84_E1 * rn / (rn + h))));
        } while (fabs(h - h2) > 1.0e-4);

        return {lat, lon, h};
    }

 这里有许多公式，知乎上有一位北大遥感的大佬对此部分做过详细的总结。

10、n系相对位置转地理坐标相对位置、地理坐标相对位置转n系相对位置

/* n系相对位置转大地坐标相对位置 */
    static Matrix3d DRi(const Vector3d &blh) {
        Matrix3d dri = Matrix3d::Zero();

        Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);

        dri(0, 0) = 1.0 / (rmn[0] + blh[2]);
        dri(1, 1) = 1.0 / ((rmn[1] + blh[2]) * cos(blh[0]));
        dri(2, 2) = -1;
        return dri;
    }

    /* 大地坐标相对位置转n系相对位置 */
    static Matrix3d DR(const Vector3d &blh) {
        Matrix3d dr = Matrix3d::Zero();

        Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);

        dr(0, 0) = rmn[0] + blh[2];
        dr(1, 1) = (rmn[1] + blh[2]) * cos(blh[0]);
        dr(2, 2) = -1;
        return dr;
    }

 11、地球自转角速度投影到e系

/* 地球自转角速度投影到e系 */
    static Vector3d iewe() {
        return {0, 0, WGS84_WIE};
    }

 12、地球自转角速度投影到n系

/* 地球自转角速度投影到n系 */
    static Vector3d iewn(double lat) {
        return {WGS84_WIE * cos(lat), 0, -WGS84_WIE * sin(lat)};
    }

    static Vector3d iewn(const Vector3d &origin, const Vector3d &local) {
        Vector3d global = local2global(origin, local);

        return iewn(global[0]);
    }

 13、n系相对于e系转动角速度投影到n系

 /* n系相对于e系转动角速度投影到n系 */
    static Vector3d enwn(const Eigen::Vector2d &rmn, const Vector3d &blh, const Vector3d &vel) {
        return {vel[1] / (rmn[1] + blh[2]), -vel[0] / (rmn[0] + blh[2]), -vel[1] * tan(blh[0]) / (rmn[1] + blh[2])};
    }

    static Vector3d enwn(const Vector3d &origin, const Vector3d &local, const Vector3d &vel) {
        Vector3d global     = local2global(origin, local);
        Eigen::Vector2d rmn = meridianPrimeVerticalRadius(global[0]);

        return enwn(rmn, global, vel);
    }

感谢武汉大学卫星导航定位技术研究中心多源智能导航实验室(i2Nav)牛小骥教授团队开源的KF-GINS软件平台。