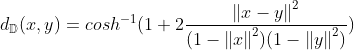Hyperbolic Nural Networks双曲神经网络

给了神经网络中一些操作的双曲版本的定义，NIPS2018的文章，原文在此：https://arxiv.org/abs/1805.09112

双曲空间在机器学习领域获得越来越多的冲力，因为它有很大的容量和它的类似于树的性质。然而，双曲几何的表达能力未能与欧式几何势均力敌，主要原因是目前还没有相应的双曲神经网络层，使得很难在下游任务中使用双曲嵌入。这里几何莫比乌斯gyrovevtor空间和双曲空间庞加莱模型的黎曼几何来定义出神经网络中的一些基础概念。最后得到双曲版本的重要的深度学习工具：多项式逻辑回归，前馈和循环神经网络单元。这能让我们在双曲空间中进行数据嵌入和进行分类。最后实验证明即使在双曲优化工具有限的情况下双曲句子嵌入也能获得与欧式嵌入相当的效果。

1简介

在机器学习领域将数据嵌入到欧式空间已经是非常常见的。主要原因是方便，欧式空间是个度量空间，有向量结构，易于计算距离和内积，是我们非常熟悉的三维空间的一般化。另外，将实体嵌入到这一连续的空间易于将它们做为神经网络的输入。

由于欧式嵌入的成功，最近的研究证明很多领域的复杂类型数据(比如图数据)表现出非欧式的隐含结构。在这样的情况下，欧式空间不能提供最大化的表达能力或者有意义的几何表示。比如，有文献证明任何树结构都不能以任意小的失真(几乎保持它原来的度量)嵌入到欧式空间中，即使用无限高维的嵌入维度。而这在双曲空间中很容易实现，只用两维的嵌入就能保证任意小的失真，这是因为双曲空间中点之间的距离是指数增长的，这正好匹配树结构中节点随树的深度指数增长的特性。

此前在非欧空间中使用神经网络和深度学习是非常受限的，主要原因是在非欧空间中没有一些基本算子(比如向量加，矩阵向量乘，向量翻译，向量内积等)的正规的定义，在一些更复杂的几何中甚至没有基本对象(如距离，测地线，平行等)的表示。这样，传统的工具如多项式逻辑回归，前馈网络或循环网络在这些几何中就没有对应的表示。

那么如何将深度神经模型泛化到非欧领域呢？本文在一个简单的同时很有用的非欧域上解决这一问题，即双曲几何中。双曲空间的树形特性已经得到了很多研究并且被用于可视化大型的分类数据或者嵌入复杂网络。在机器学习方面，最近双曲空间在分层、分类或者继承数据上的表现远远超过了欧式空间。隐含的分层结构中不相交的子树在嵌入空间中得到了很好的聚类。然而，为了嵌入特征数据和在下游任务中使用这些嵌入，合适的深度学习工具是必要的。比如，隐式的分层序列结构在合适的双曲RNN中将会得到更好的建模。

本文的主要贡献是在神经网络和深度学习的背景下建立双曲空间和欧式空间之间的鸿沟，以规范的方式将基本的算子和多项式回归、前馈网络、RNN和GRU泛化到双曲几何中的庞加莱模型中。主要将gyrovector空间和泛化的莫比乌斯转换与流行的黎曼几何特性相结合。利用一个只依赖于曲率值的统一的框架平滑地参数化所有常数负曲率空间的基本操作和对象。这样，欧式空间和双曲空间可以连续地转换。

2 庞加莱球几何

2.1基本的黎曼几何

       一个n维流形M 是一个可以被欧式空间局部近似的空间。对于流形中的一个点,我们可以定义  在  点的切空间做为  在  点的一阶线性近似。上的黎曼度量  是随 x 平滑变化的一些内积：。一个黎曼流形  是一个具有黎曼度量流形。尽管上的黎曼度量只定义在的局部，在结合两点间的最短路径的长度之后，它可以诱导出全局距离。

                                                                 

其中且. x 和 y之间的平滑的最短路径  叫做测地线，可以看做欧氏空间中直线的泛化。平移 是切空间之间的线性等距，相当于沿测地线移动切向量，这定义了连接两个切空间的一种方式。x点的指数映射  提供了将x点的切空间中的向量映射回流形中的点的一种方式。对于测地线完备的流形（比如庞加莱球）来说，在整个切空间上都有定义。最后，一个度量与另一个度量定义了同样的角，则称为是保角的，即对于所有的

                                                                  

这相当于存在一个光滑的函数,称为保角因子，使得对于任何，有

2.2双曲空间：庞加莱球

双曲空间中有五个等距的模型，这里选择庞加莱球，庞加莱球模型由流形

                                                                

和黎曼度量

                                                                         

定义出来，其中,而  是欧氏度量张量。注意双曲度量张量保角于欧氏度量，庞加莱球上两点之间的诱导距离就由以下式子给出:

                                                              

由于庞加莱球是保角于欧氏空间的，所以向量之间的夹角为：

                                                           

2.3 Gyrovector 空间

在欧氏空间中，从向量结构引申出来的自然操作(如向量加、减和标量乘)通常非常有用，在双曲几何中， Gyrovector 空间提供了相应的代数形式。实际上，这些操作在狭义相对论中有使用，允许将半径为c的庞加莱球上的速度向量相加。这里将这些操作用于双曲神经网络。

对于定义

                                                                               

注意，如果则;如果则是半径为的球；如果则又恢复成一般的球

莫比乌斯加:

上两点x,y的莫比乌斯加定义为：

                                                         

特3别地，当变成欧氏空间中两个向量的加，注意包含的情况，下文用代替.对于一般的的情况，这个算子既不满足交换律也不满足结合律，但有以下的特殊情况:

                                                                                     

,另外，对于任意的,有

                                                                               

和

                                                                                        

莫比乌斯标量乘：

对于 , 莫比乌斯标量乘定义为:

                                                                

由此我们得到   和   ,即当c趋于0时，莫比乌斯标量乘蜕化为欧氏空间中的标量乘。这个算子满足一下性质：

(1)n加：

(2)分配律：

(3)结合律：

(4)标度性：

距离:

如果双曲度量张量  以保角因子保角与欧氏空间,则上的距离函数为：

                                                                         

同样，我们有, 即又恢复了欧氏几何。另外，c=1时恢复正常的庞加莱球上的距离

2.4 Gytovector sapces 和庞加莱秋上黎曼几何的关系

测地线：

连接点的测地线定义为：

                                                                               

其中,使得

当c趋于0时，测地线变成直线，恢复为欧氏几何。

exp映射和log映射：

对于任意的点,exp映射 和log映射定义为：

                                                                     

                                                               

当x=0时，形式如下：

                                                                          

                                                                          

用exp和log 重新定义莫比乌斯标量乘法：

引理： 可以通过以下方式得到：用log映射将x映射到0点的空间上，在切空间上乘以标量r，然后再用exp映射映射回流形上，即

                                                                  

另外，我们还可以得到链接两点的测地线和exp映射的关系：

                                                                

这个结果使得我们将标量乘进行泛化，以定义出矩阵-向量乘法，而这样的乘法是双曲神经网络的基本组件。

平移：

在流形上，一个向量到另一个切空间的平移定义为：

                                                                  

这一结果在定义和优化不同切空间的共享参数时非常有用。

3 双曲神经网络

神经网络可看作由基本的算子(比如线性映射，偏置转换，逐点非线性激活和最终的sigmoid或softmax层)组合而成。下面首先解释如何在庞加莱球上构建softmax层，然后定义庞加莱球上的矩阵-向量乘和逐点的非线性激活。最后呈现出不同的RNN如何在庞加莱球上的对应。

3.1双曲多分类逻辑回归

没看懂

3.2双曲前馈层：

定义:对于,它的莫比乌斯版本定义为从到的映射：

                                                                                

与其他莫比乌斯算子一样，当c趋于0时，有

莫比乌斯矩阵-向量乘：

如果是用矩阵形式表示的线性映射，则,如果,则有

                                                         

如果,则有

另外，如果莫比乌斯矩阵-向量乘定义为

                                                                           ,

则对于,有

                                                                 

对于,有

                                                                    

逐点的非线性激活：

如果是逐点的非线性激活，则它的莫比乌斯版本  可以应用与庞加莱球上的点。

偏置：

庞加莱球上的平移通过在测地线上移动来实现。点经过偏置的莫比乌斯平移为：

                                                    

多个输入张量的连接

如果,矩阵是二者的水平方向上的连接，则对于,有

                                                                    

3.3双曲RNN

原始的RNN：

对于,双曲RNN定义为：

                                                 

如果输入特征是欧氏空间的，则可先通过映射到双曲空间，再代入上式。

GRU

欧氏空间中的GRU架构为：

                                                

其对应的双曲版本分别为：

                                                          

                                                       

                                                              

与类似。