使用卡方分箱进行数据离散化-python实现
我们经常疑惑,有些算法例如逻辑回归评分卡建模时为什么要用分箱技术。搞懂了离散化优点即可找到答案。
离散化(Discretization):将定量数据转化为定性数据的过程。
-
一些数据挖掘算法只接受分类属性(LVF、FINCO、朴素贝叶斯)。
-
当数据只有定量特征时,学习过程通常效率较低且效果较差。
卡方分箱算法(Chi Merge Algorithm)
-
这种离散化方法使用合并方法。
-
相对类频率应该在一个区间内相当一致(否则应该分裂)
-
χ2 是用于检验两个离散属性在统计上独立的假设的统计量度。
-
对于相邻的两个区间,如果 χ2 检验得出该类是独立的区间,则应合并。如果 χ2 检验得出的结论是它们不是独立的,即相对类别频率的差异在统计上是显着的,则两个区间应保持独立。
(卡方分布图)
列联表
计算 χ 2
值可以计算如下:
计算步骤
-
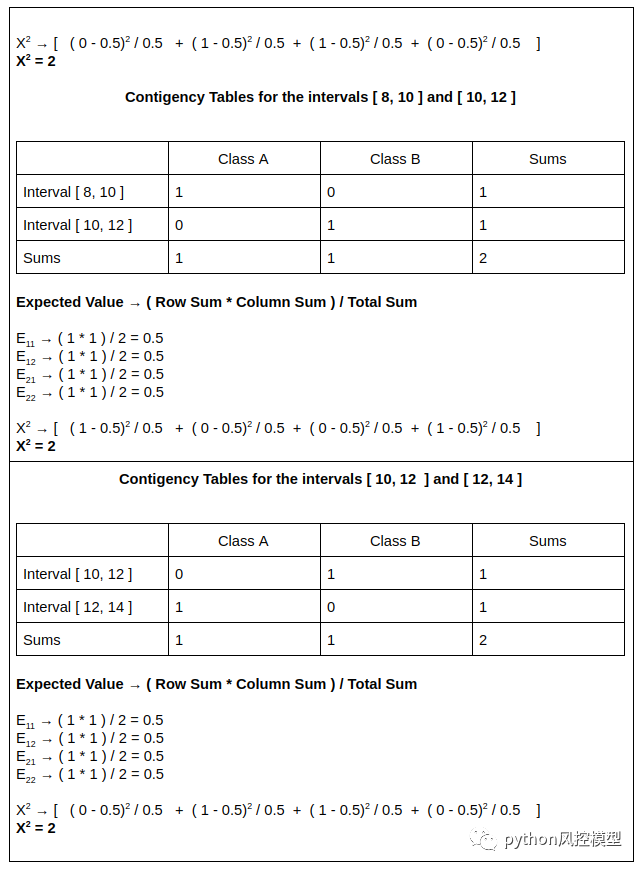
计算每对相邻区间的 χ2 值
-
合并具有最低 χ2 值的相邻区间对
-
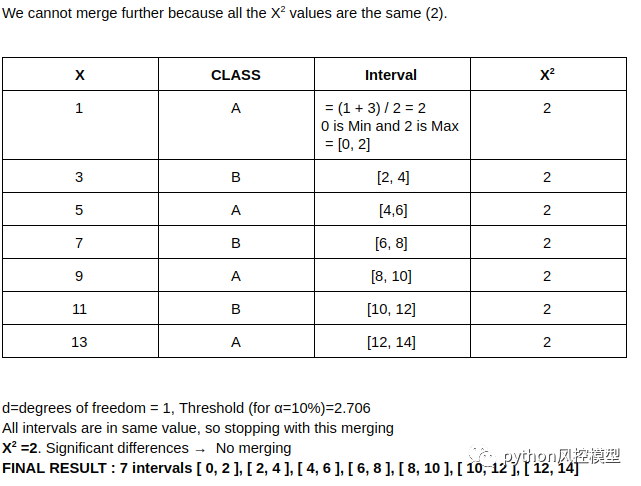
重复上述步骤,直到所有相邻对的χ2值超过阈值
-
阈值:由显着性水平和自由度决定 = 类数 -1
例子
Chi Merge卡方分箱 的示例
Chi Merge 进行如下。最初,数值属性 A 的每个不同值都被认为是一个区间。对每对相邻区间进行 χ2 检验。具有最小 χ2 值的相邻区间合并在一起,因为一对的低 χ 2 值表示相似的类分布。这个合并过程递归进行,直到满足预定义的停止标准。
- 第1步
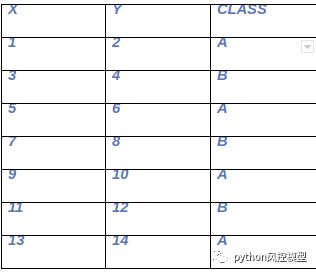
将数据集拆分为 2 个数据集并分别查找值。
数据集 1 → X,类
数据 集 2 → Y,类
使用 Python 实现的 Chi Merge卡方分箱
让我们使用 IRIS 数据集并尝试实施 Chi Merge 过程。
python scipy包有卡方检验函数
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html
#微信公众号:python风控模型
import scipy.stats as stats
data = np.array([[43,9],
[44,4]])
V, p, dof, expected = stats.chi2_contingency(data)
print(p)
更多卡方检验代码
# -*- coding: utf-8 -*-
'''
腾讯云课堂:python金融风控评分卡模型和数据分析:
https://edu.csdn.net/combo/detail/1927
微信公众号:python风控模型
'''
'''
卡方公式(o-e)^2 / e
期望值和收集到数据不能低于5,o(observed)观察到的数据,e(expected)表示期望的数据
(o-e)平方,最后除以期望的数据e
'''
import numpy as np
from scipy import stats
from scipy.stats import chisquare
list_observe=[30,14,34,45,57,20]
list_expect=[20,20,30,40,60,30]
std=np.std(data,ddof=1)
print(chisquare(f_obs=list_observe, f_exp=list_expect))
p=chisquare(f_obs=list_observe, f_exp=list_expect)[1]
'''
返回NAN,无穷小
'''
if p>0.05 or p=="nan":
print"H0 win,there is no difference"
else:
print"H1 win,there is difference"
此版本不用算出期望值,更加方便,参考的是2*2联立表,自由度=1,critical value=2.7
# -*- coding: utf-8 -*-
'''
腾讯云课堂:python金融风控评分卡模型和数据分析:
https://edu.csdn.net/combo/detail/1927
微信公众号:python风控模型
'''
#独立性检验test for independence,也是卡方检验chi_square
#前提条件:a,b,c,d 必须大于5
#2.706是判断标准(90概率),值越大,越有关,值越小,越无关
def value_independence(a,b,c,d):
if a>=5 and b>=5 and c>=5 and d>=5:
return ((a+b+c+d)*(a*d-b*c)**2)/float((a+b)*(c+d)*(a+c)*(b+d))
#返回True表示有关
#返回False表示无关
def judge_independence(num_independence):
if num_independence>2.706:
print ("there is relationship")
return True
else:
print("there is no relationship")
return False
a=34
b=38
c=28
d=50
chi_square=value_independence(a,b,c,d)
relation=judge_independence(chi_square)
使用卡方分箱进行数据离散化就为大家介绍到这里。强调一下,并非所有算法都需要数据离散化处理。目前集成树算法也很流行,例如xgboost,lightgbm,catboost,他们都不需要数据离散化处理。到底哪种方法最好,这个说不准,我通过多个项目测试,不同数据分布有不同结论!希望各位同学不要盲目迷信理论,自己多去做测试,多自我思考。
使用卡方分箱进行数据离散化就为大家介绍到这里了,欢迎各位同学报名
https://edu.csdn.net/combo/detail/1927

版权声明:文章来自公众号(python风控模型),未经许可,不得抄袭。遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。