如何进行反欺诈风控模型冷启动

在金融反欺诈风控业务场景下，由于欺诈风险的类型较为复杂且多变，因此常常会在样本数据的好坏标签严重不足，甚至是标签缺失的情况下进行模型开发工作，这种现象被称为模型冷启动。本文将结合实际业务场景，给大家介绍下反欺诈风控模型冷启动的思想与方法。

1、冷启动建模背景
在正式介绍冷启动的建模方案之前，先简单梳理下常规情况的金融风控建模流程，具体步骤如下：
（1）定义明确的因变量Y，即好坏标签；
（2）根据建模数据划分训练数据集、验证数据集和测试数据集，其中测试数据集和训练、验证数据集的采样时间段不同；
（3）自变量特征X的数据清洗，包括但不限于缺失值处理、异常值处理、数据变换等；
（4）自变量特征X的筛选，采用相关分析、卡方检验等方式，选取与目标变量Y关系较强的特征变量；
（5）采用不同的模型算法（如逻辑回归、XGBoost等）对训练数据集进行模型拟合，并结合验证数据集进行参数调优；
（6）在测试数据集上跑模型，测试模型的区分度和稳定性等综合效果；
（7）正式部署上线模型。
在风控模型冷启动的场景下，上述流程中的第1步，即因变量的好坏标签目前是严重缺失的状态。针对如何确定样本数据的好坏标签，一般存在两种建模方案，一种是基于实际业务经验给出样本的好坏标签，另一种是基于机器学习模型预先对标签进行分析与判断。

2、方案1：标准有监督学习
以某银行信用卡盗刷识别业务场景为例，其业务核心为反欺诈风控，建模将非本人交易作为模型的预测目标，针对实际业务抽取一定数量样本进行模型拟合训练，另在其他时间段抽取一定数量的样本用于模型测试。金融机构根据上述样本数据，基于实际业务的“专家”经验提供明确的好坏标签，例如信用卡在本人手中但本人未有消费行为、消费签名非本人所签等情况下的特征表现。然后，根据明确的好坏样本，按照常规建模流程进行有监督学习建模，例如采用逻辑回归、XGBoost等分类算法拟合模型，当模型训练完成后，便可以对盗刷交易进行预测识别。关于模型的泛化能力和稳定性能的检测，通过测试数据集，带入模型计算KS、AUC和PSI等指标来完成。测试样本选用与训练样本完全不同的时间段数据。
如果在实际场景中方案1在实施上有困难，也就是根据业务经验难以判断样本反欺诈的好还标签时，则只能基于数据本身进行半监督学习，对样本进行标签赋值，详见方案2介绍。

3、方案2：半监督学习~模型多轮迭代
本场景仍以某银行信用卡盗刷识别业务为例，反欺诈模型将非本人交易作为建模的预测目标，建模样本数据可以被分为以下两大类别：
类1：每月规则拦截后接电话的交易（根据电核结果确认本人交易/非本人交易）；
类2：规则未拦截+电核未接听的交易（无法充分判断是否本人交易）。
对于1类样本的好坏标签已经明确无误，但是客群仅为规则拦截后接听电话的用户，样本数量并不很多。如果基于此种情形进行建模，必然存在很大的模型过拟合风险，使得模型在全体用户交易样本上的应用，效果性能表现不佳。因此，在实际业务中，必须考虑在1类样本的基础上，采用半监督学习的思想，加入2类样本的数据信息进行辅助建模。
在建模过程中，最直接的处理方式是根据1类好坏样本的数据信息，对2类样本进行人工好坏区分，具体建模流程可以是：
（1）基于1类样本（已有明确标签），采用逻辑回归算法训练模型，接着在2类样本上进行概率输出；
（2）基于1类样本信息对2类样本进行KNN分类标注，可得到2类样本的好坏标签；
（3）将1类、2类样本混合，采用分类算法进行模型训练，得到反欺诈分类预测模型；
（4）使用新得到的分类模型对2类样本再次标注，接着进行多次迭代后可得到较为稳定的模型结果。
对于以上方案，介绍了基于模型多轮迭代思想下的反欺诈风控冷启动方案，用以解决样本好坏标签缺乏的实际情形（1类样本有标签但数量不足，2类样本无标签但数量很多）。这里需要注意到是，采用这种方案需要有个合理性的前提假设，即1类样本和2类样本的自变量特征分布是相同的，差异仅仅在于2类无好坏标签。因此可以根据1类样本的自变量数据特征与好坏标签的关系，直接类比推广到2类样本上，从而补齐2类样本的好坏标签。

4、方案3：半监督学习~迁移学习
对于方案2的解决流程，在实际场景中上述前提假设可能有误，即1类样本和2类样本的特征分布并不相同。由于两类样本的来源不同，1类是规则拦截后接听电核的客群，2类是规则未拦截+拦截未接听电核的客群，特征分布相同假设是否成立通常难以直接下判断。
针对两类样本分布不同的情况，可以采用迁移学习来进行半监督模型开发，大体步骤为以1类样本为源域数据，2类样本为目标域数据，进行JDA半监督迁移学习。下面简要描述下JDA迁移学习算法的核心思想：
（1）JDA迁移学习算法的概念：
对于建模样本，源域数据Ds={(xs1,ys1),(xs2,ys2),…（xsn,ysn）}，目标域数据Dt={xt1,xt2,…,xtn2}。其中源域数据个数为n1，目标域数据个数为n2。Ps(xs)是Ds的边缘概率分布，Pt(xt)是Dt的边缘概率分布， Ps(ys|xs)是Ds的条件概率分布， Pt(yt|xt) 是的Dt条件概率分布（目标域数据Dt中一开始不存在yt）。
（2）JDA迁移学习算法的假设：
源域和目标域的特征空间和标签空间一致,但是Ps (xs)≠Pt (xt)，Ps (ys|xs)≠Pt (yt|xt)，且目标域数据Dt中初始无标签。此处存在一个映射f，可以使得Ps (f(xs))≈Pt (f(xt))，Ps (ys |f(xs))≈Pt (yt |f(xt))，该假设和目前的建模数据场景吻合。
（3）JDA迁移学习算法的目标：
数据属性保留。JDA通过最大化映射后数据方差来保留数据属性。该问题转化为PCA进行求解。设X=[x1,…,xn]∈Rmn，其中n=n1+n2，m是自变量特征维度，H为中心化矩阵，协方差矩阵为：XHXT，A为转换矩阵，则问题化为maxAT A=1 tr(A^T XHX^T A)，取最大的k个特征值对应的特征向量组成矩阵A∈Rmk，映射后的数据为Z=AT X，Z∈Rk*n。
缩小边缘概率分布差异。JDA采用MMD距离来衡量Ps(ATxs)和Pt(ATxt)的差异，问题转化为：minA||1/n1 ∑N1AT xi -1/n2 ∑N2AT xj ||2，其中N1={1,…,n1}，N2={n1+1,…,n}。通过该目标函数，映射后的数据Z中源域数据与目标数据的边缘概率分布差异最小。
缩小条件概率分布差异。首先基于源域数据训练一个分类模型，给目标域数据打伪标签，利用伪标签计算目标域数据的条件概率分布。由于Pt(ATxt|yt)和Ps(ATxs|ys)难以计算，JDA分别以用和作为充分统计量来代替计算。问题化为：对于标签空间{1,2,…,C}，有∑c∈CminA||1/n1c ∑xi∈DscAT xi -1/n2 ∑xj∈DtcAT xj ||2。
针对上述三个目标，最终算法的优化目标为：minA∑c=0C tr(AT XHXT A)+λ‖A‖2F,s.t.AT XHXT A=I。目标函数第二项为正则项，第一项代表源域数据和目标域数据的边缘概率分布与条件概率分布的MMD距离求和，推导过程略，主要是基于性质‖A‖2=tr(AAT)和tr(AB)=tr(BA)。此处c从0开始，c=0则代表边缘概率分布那一项。
根据拉格朗日乘子法，求导后得：(X∑c=0CMc XT +λI)A=XHXT Aϕ，其中ϕ为拉格朗日乘子矩阵。只需对(XHXT)-1 (X∑c=0CMc XT +λI)进行特征分解，取最大的k个特征值对应的特征向量组成A即可。
上述过程是基于线性映射出发，也可以考虑非线性映射。对于非线性映射采用经验核映射，算法的最终优化目标函数形式可以转换为：minA ∑c=0Ctr(AT KMc KT A)+λ‖A‖2F ,s.t.AT KHKT A=I，其中K为选用的核矩阵，其余求解方式和前述一样。为了得到更为稳定的模型结果，也可以基于JDA计算后的数据，迭代更新数次伪标签。

5、方案对比分析
对于以上方案2（半监督学习-模型多轮迭代）与方案3（半监督学习–迁移学习），在具体实践中需要结合样本数据的分布情形，现简要对比下两种算法方案思想的优缺点，如下表所示：
​

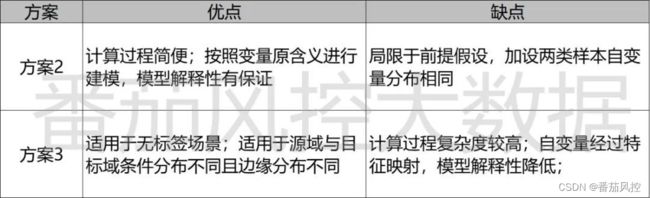
从上表可知，在建模两类样本自变量特征分布相同的前提下，解决方案2是更优的选择。因此，在自变量数据加工完毕后，首先需要对样本数据分布进行相似性上的检测（1类2类样本同一变量的非参数检验）。鉴于自变量数量较多，可以先基于1类样本进行变量挑选（单变量逻辑回归系数显著性、决策树输出变量重要性、好坏样本的非参数检验），将入模变量限定在一定数量范围内，再进行自变量数据分布相似性的检测分析。
如果1类与2类样本自变量的数据分布大体相似，则采用方案2进行建模，否则采用方案3。另外，还需要根据具体模型效果上的性能差异，来综合判断哪种方案的结果更优。例如，若采用逻辑回归算法得到的模型效果已经达到要求，考虑到模型较好的解释性能，可以尽量考虑方案2。但是如果必须通过使用XGBoost等解释性本身较弱的算法，才能达到预测分类模型的准确性要求，则直接使用方案3更适合些。

6、冷启动后续工作
在以上冷启动情景的反欺诈建模方案中，显然半监督迁移学习算法更贴近实际业务的特点，即采用手工打标签的方式，能够帮助此次业务实现冷启动。但是，模型仅能观察到在训练集与验证集上的运行效果，而无法预先做泛化方面的测试，需要在将来实际上线应用中进行模型泛化测试，具体步骤为：
（1）模型上线后识别出的危险交易行为，银行方通过电核方式，确认是否非本人交易，从而为样本打上好坏标签；
（2）针对规则拦截的样本，接着采用电核方式来判断是否非本人交易；
（3）收集一定时间（比如3个月、6个月）的样本后，进行模型泛化能力测试和模型稳定性测试，分析模型在新样本上的KS、AUC、PSI等指标；
（4）当模型各指标表现良好则模型暂无问题，否则可能需要再次更新迭代模型。

关于本文中所提到的关于反欺诈等相关体系化内容，也欢迎同步来学习番茄风控的系列性内容，分别是：

①风控反欺诈训练营

​
②全线条训练营
​
…

~原创文章