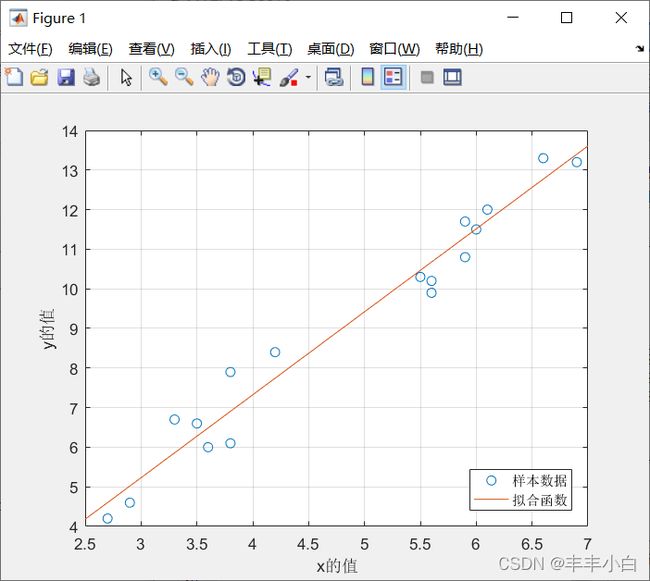
拟合算法之最小二乘法
拟合算法
与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是追求一个函数(曲线),使得该曲线在某种准测下与所有的数据点最为接近,即曲线拟合最好(最小化损失函数)。
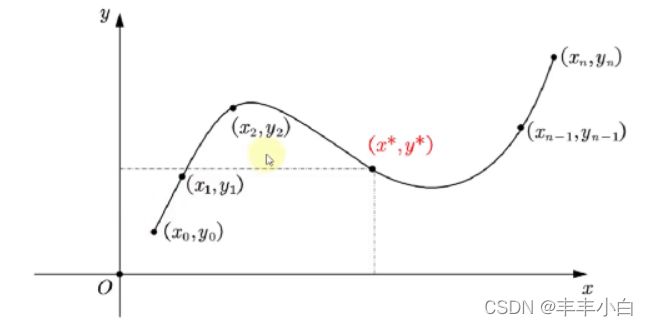
插值算法中,得到的多项式f(x)要经过所有的样本点。但是如果样本点太多,那么这个多项式的次数过高,会造成龙格现象。
尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更要倾向于得到一个确定的曲线,尽管这条曲线不能经过每一个样本点,但只要保证误差足够小即可,这就是拟合的思想。(拟合的结果是得到一个确定的曲线)
最小二乘法
设这些样本点为(xi,yi),i=1,2,3,…,n
我们设置拟合的曲线为y=kx+b,求当k和b为何值时,样本点和拟合曲线最接近。
第一种定义: y ^ i = k x i + b \widehat{y}_i=kx_i+b y i=kxi+b
k ^ , b ^ = a r g k , b m i n ( ∑ i = 1 n ∣ y i − y ^ i ∣ ) \widehat{k},\widehat{b}=arg_{k,b}min(\sum_{i=1}^n{|y_i-\widehat{y}_i|}) k ,b =argk,bmin(i=1∑n∣yi−y i∣)
第二种定义: y ^ i = k x i + b \widehat{y}_i=kx_i+b y i=kxi+b
k ^ , b ^ = a r g k , b m i n ( ∑ i = 1 n ( y i − y ^ i ) 2 ) \widehat{k},\widehat{b}=arg_{k,b}min(\sum_{i=1}^n{(y_i-\widehat{y}_i)^2}) k ,b =argk,bmin(i=1∑n(yi−y i)2)
第一种定义有绝对值,不容易求导,因此计算比较复杂。所以我们往往使用第二种定义,这也是最小二乘的思想。
为什么不用四次方?
① 避免极端数据对拟合曲线的影响。
② 最小二乘法得到的结果和MLE极大似然估计一致。
③ 奇数次方误差会正负相抵。
设这些样本点为 ( x i , y i ) , i = 1 , 2 , 3... , n (x_i,y_i),i=1,2,3...,n (xi,yi),i=1,2,3...,n
我们设置拟合的曲线为 y = k x + b y=kx+b y=kx+b。令拟合值为: y ^ i = k x i + b \widehat{y}_i=kx_i+b y i=kxi+b
那么我们就可以得到:
k ^ , b ^ = a r g k , b m i n ( ∑ i = 1 n ( y i − y ^ i ) 2 ) = a r g k , b m i n ( ∑ i = 1 n ( y i − k x i − b ) 2 ) \widehat{k},\widehat{b}=arg_{k,b}min(\sum_{i=1}^n{(y_i-\widehat{y}_i)^2})=arg_{k,b}min(\sum_{i=1}^n{(y_i-kx_i-b)^2}) k ,b =argk,bmin(i=1∑n(yi−y i)2)=argk,bmin(i=1∑n(yi−kxi−b)2)
令 L = ∑ ( y i − k x i − b ) 2 L=\sum{(y_i-kx_i-b)^2} L=∑(yi−kxi−b)2,要实现找到 k , b k,b k,b使得 L L L最小。( L L L在机器学习中被称为损失函数,在回归中也常被称为残差平方和)
接下来使 L L L对 k k k和 b b b进行求导:
{ ∂ L ∂ k = − 2 ∑ i = 1 n x i ( y i − k x i − b ) = 0 ∂ L ∂ k = − 2 ∑ i = 1 n x i ( y i − k x i − b ) = 0 \left\{ \begin{aligned} \frac{\partial L}{\partial k }=-2\sum_{i=1}^nx_i(y_i-kx_i-b)=0 \\ \frac{\partial L}{\partial k }=-2\sum_{i=1}^nx_i(y_i-kx_i-b)=0 \\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂k∂L=−2i=1∑nxi(yi−kxi−b)=0∂k∂L=−2i=1∑nxi(yi−kxi−b)=0
得到:
k ^ = n ∑ i = 1 n x i y i − ∑ i = 1 n y i ∑ i = 1 n x i n ∑ i = 1 n x i 2 − ∑ i = 1 n x i ∑ i = 1 n x i \widehat{k}=\frac{n\sum\limits_{i=1}^nx_iy_i-\sum\limits_{i=1}^ny_i\sum\limits_{i=1}^nx_i}{n\sum\limits_{i=1}^nx_i^2-\sum\limits_{i=1}^nx_i\sum\limits_{i=1}^nx_i} k =ni=1∑nxi2−i=1∑nxii=1∑nxini=1∑nxiyi−i=1∑nyii=1∑nxi
b ^ = ∑ i = 1 n x i 2 ∑ i = 1 n y i − ∑ i = 1 n x i ∑ i = 1 n x i y i n ∑ i = 1 n x i 2 − ∑ i = 1 n x i ∑ i = 1 n x i \widehat{b}=\frac{\sum\limits_{i=1}^nx_i^2\sum\limits_{i=1}^ny_i-\sum\limits_{i=1}^nx_i\sum\limits_{i=1}^nx_iy_i}{n\sum\limits_{i=1}^nx_i^2-\sum\limits_{i=1}^nx_i\sum\limits_{i=1}^nx_i} b =ni=1∑nxi2−i=1∑nxii=1∑nxii=1∑nxi2i=1∑nyi−i=1∑nxii=1∑nxiyi
这里我们给出一组数据,使用matlab,来用最小二乘法拟合一下
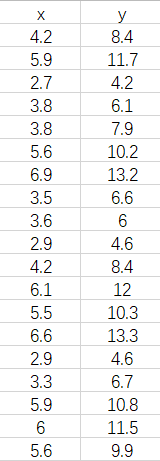
clear;clc
load data1
plot(x,y,'o') % 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
得到散点图: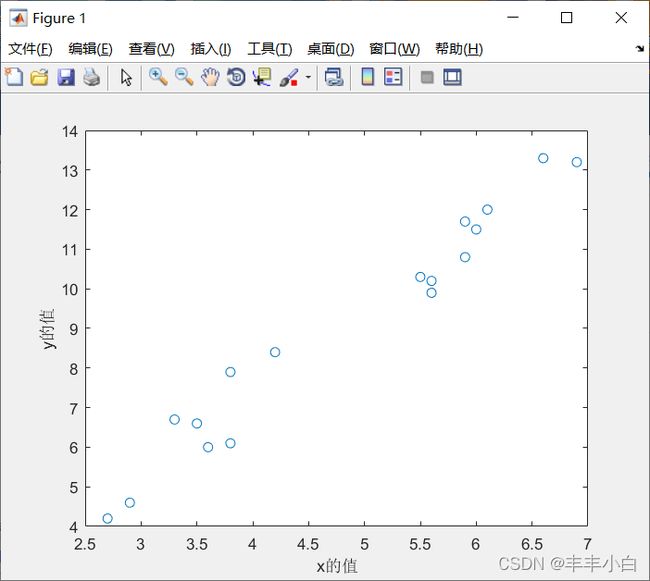
接下来利用公式得到k和b的值,并利用匿名函数画出拟合后的函数图像:
clear;clc
load data1 %事先将x和y保存到data1中,也可以直接输入
plot(x,y,'o') % 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')
拟合好坏的评价:拟合优度
如何来评价拟合的程度,我们使用拟合优度(可决系数) R 2 R^2 R2。首先我们引入几个定义:
总 体 平 方 和 S S T : S S T = ∑ i = 1 n ( y i − y ˉ ) 2 总体平方和SST:SST=\sum\limits_{i=1}^n(y_i-\bar{y})^2 总体平方和SST:SST=i=1∑n(yi−yˉ)2
误 差 平 方 和 S S E : S S E = ∑ i = 1 n ( y i − y ^ i ) 2 误差平方和SSE:SSE=\sum\limits_{i=1}^n(y_i-\widehat{y}_i)^2 误差平方和SSE:SSE=i=1∑n(yi−y i)2
回 归 平 方 和 S S R : S S R = ∑ i = 1 n ( y ^ i − y ˉ ) 2 回归平方和SSR:SSR=\sum\limits_{i=1}^n(\widehat{y}_i-\bar{y})^2 回归平方和SSR:SSR=i=1∑n(y i−yˉ)2
可以证明: S S T = S S E + S S T SST=SSE+SST SST=SSE+SST(用到我们求导得到的两个等式)
拟 合 优 度 : 0 ≤ R 2 = S S R S S T = S S T − S S E S S T = 1 − S S E S S T ≤ 1 拟合优度:0\leq R^2=\frac{SSR}{SST}=\frac{SST-SSE}{SST}=1-\frac{SSE}{SST}\leq 1 拟合优度:0≤R2=SSTSSR=SSTSST−SSE=1−SSTSSE≤1
R 2 R^2 R2越接近1,说明误差平方和越接近0,误差越小说明拟合的越好。
(注: R 2 R^2 R2只能用于拟合参数线性函数,拟合结果的评价)
线性函数和其他函数(例如指数函数)比较拟合的好坏,直接看 S S E SSE SSE即可(越小越好),未来还可能遇到 R 2 R^2 R2是负数的情况。
使用matlab计算 R 2 R^2 R2:
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差,可以忽略不计,说明SST=SSE+SSR
R_2 = SSR / SST
注:mean是平均值
最小二乘法的拟合到这里就结束啦,喜欢的小伙伴可以点个关注,下一讲:使用matlab进行图像拟合。