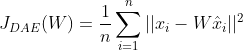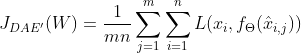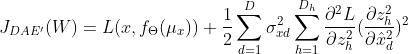正则自编码器之去噪自编码器

图1.自编码器的一般结构

传统自编码器通过最小化如下目标：

                                                  (公式1)

公式1中L是一个损失函数，惩罚g(f(x))与x的差异，如它们彼此差异的L2范数。若自编码器容量过大，则其将学到一个毫无意义的恒等式。

去噪自编码器的定义：

去噪自编码器是一类接受损坏数据作为输入，并训练来预测原始未受损数据作为输出的自编码器。

去噪自编码器(Denoising autoencoder,DAE)的最小化目标如下式：

                                                   (公式2)

公式2中表示被某种噪声损坏的x的副本，去噪自编码器必须学会撤销这些损坏，而不是简单的复制输入。

去噪训练过程强制f 和 g 隐式的学习的结构。所以，去噪自编码器也是一个通过最小化重构误差获取有用特性的例子。

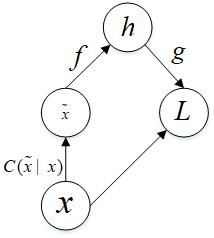
图2.去噪自编码器代价函数的计算图

如图2所示，相较与传统自编码器，去噪自编码器引入了一个损坏过程，这个条件分布代表给定数据样本X产生损坏样本的概率。自编码器则根据如下过程，从训练数据对中学习重构分布：

1.从训练数据中采一个训练样本；

2.从采一个损坏样本；

3.将作为训练样本来估计自编码器的重构分布，其中h是编码器的输出，根据解码函数定义。

通常可以简单的地对负对数似然进行基于梯度法的近似最小化。只要编码器是确定性的，去噪自编码器就是一个前馈神经网络，可以使用与其他前馈神经网络完全相同的方式进行训练。

去噪自编码器在如下式所示的期望下进行随机梯度下降：

              (公式3)

为了使重构数据与原始未受损数据之间的误差尽可能的小，去噪自编码器的的目标是最小化损失函数：                                       (公式4)

综上所述，去噪自编码器通过对输入信号人为地进行损坏，主要是为了：1.避免使自编码器学习到一个没有任何实际意义的恒等式；2.使隐藏层神经单元可以学习到一个更加具有鲁棒性的特征表达。

领域适应性边缘去噪自编码器(Marginalized Denoising Autoencoders for Domain Adaption)

领域适应性边缘去噪自编码器由Chen等人提出，主要目的是解决去噪自编码器存在的两个关键缺陷：1.计算代价高；2.缺少对高维特征的可伸缩性。领域适应性去噪自编码器通过将噪声边缘化(?)，使得在算法中不需要使用任何优化算法来学习模型中的参数，提高网络的训练速度。

MDADA自编码器由若干个单层去噪自编码器组合而成，因此它的输入信号与去噪自编码器的输入信号相同，都是经过加噪处理后的损坏信号。如果采用平方重构误差作为损失函数，则MDADA的目标就是最小化下式：

                                       (公式5)

为了将模型更具普遍性，会将实验过程重复m次，每次添加不同的噪声，产生m个不同的受损数据作为输入，由此公式5可以改写为最小化整体平方重构误差：

                           (公式6)

其中为原始未受损输入的第j个损坏版本。

根据范数与矩阵之间的关系，公式6可以进一步改写为下式：

                   (公式7)

其中，，具有m个元素，是与对应的损坏版本，tr(A)表示求矩阵A的迹(在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A))。由此，MDADA的损失函数可转换为求解下式：

                                                                           (公式8)

其中，。

根据弱大数定律，当实验次数m足够大时，公式8中的P,Q最终会分别收敛于它们的期望值，因此令，公式8可以转换为：

                                                              (公式9)

其中，                                                    (公式10)

                                      (公式11)

在公式10与公式11中，表示特征不被损坏的概率，表示特征不被损坏的概率。

最后可以通过式9计算出网络参数W，通过上述可以知道求解网络参数的过程中没有使用任何的优化算法，仅需要遍历训练数据一次就可以求得E[P]与E[Q]的值，这是MDADA自编码器极大缩短训练时间的原因。

领域适应性边缘降噪自编码器具有比较强的学习能力，训练速度快，更少的中间参数，更快的模型选择以及基于逐层训练的凸性，但缺点在于只能用线性表示。

非线性表示边缘去噪自编码器(Marginalized Denoising Autoencoders for Nonlinear Representation)

为克服领域适应性边缘去噪自编码器只能用线性表示的缺点，chen等人提出了非线性表示边缘去噪自编码器(MDANR)。MDANR与MDADA算法的最大区别在于将噪声进行边缘化处理时，改为利用去噪自编码器损失函数的泰勒展开式来近似表示其期望损失函数。

去噪自编码器的目标函数的更加普遍形式：

                          (公式12)

公式12中L可以是平方重建误差损失函数，或者交叉熵损失函数。

与MDADA算法同理，使用弱大数定理，利用无穷多个损坏数据将优化问题转换为期望问题，因此在满足损失分布条件下，公式12可以转换为期望问题：

                             (公式13)

在上利用泰勒展开式，对公式13中的损失函数L进行展开并加上期望可得：

      (公式14)

公式14中，与是损失函数L关于的一阶和二阶导数，因为，所以。

---

完整推导过程可以参见袁非牛等《自编码神经网络理论及应用研究综述》

最后可得，非线性表示边缘去噪自编码器的目标函数为;

             (公式14)

其中是对角线上第d项，即第d维输入的噪声损坏方差。公式14实则是在去噪自编码器的损失函数上添加了一个正则项，该正则项考虑了重建函数对隐藏层表达的敏感度，同时考虑了隐藏层表达对输入的损坏信号的敏感度。

参考文献：袁非牛《自编码神经网络理论及应用研究综述》