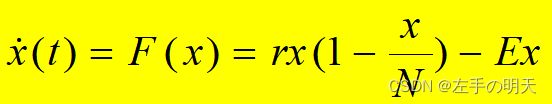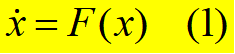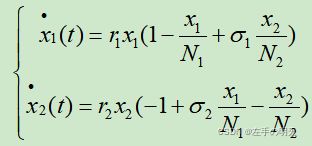数学建模之稳定性模型详解
码字总结不易,老铁们来个三连:点赞、关注、评论
作者:[左手の明天]
原创不易,转载请联系作者并注明出处
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
对象仍是动态过程,而建模目的是研究时间充分长以后过程的变化趋势 ——平衡状态是否稳定。
不求解微分方程,而是用微分方程稳定性理论研究平衡状态的稳定性。
目录
捕鱼业的持续收获
产量模型
假设
建模
一阶微分方程的平衡点及其稳定性
效益模型
捕捞过度
捕鱼业的持续收获
matlab验证
军备竞赛
目的
假设
建模
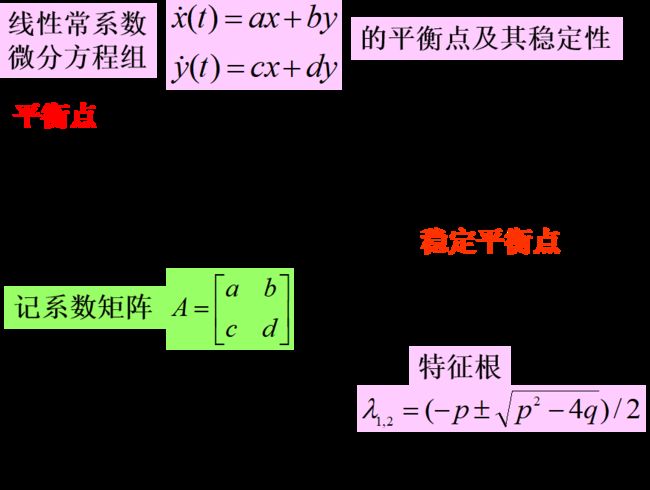
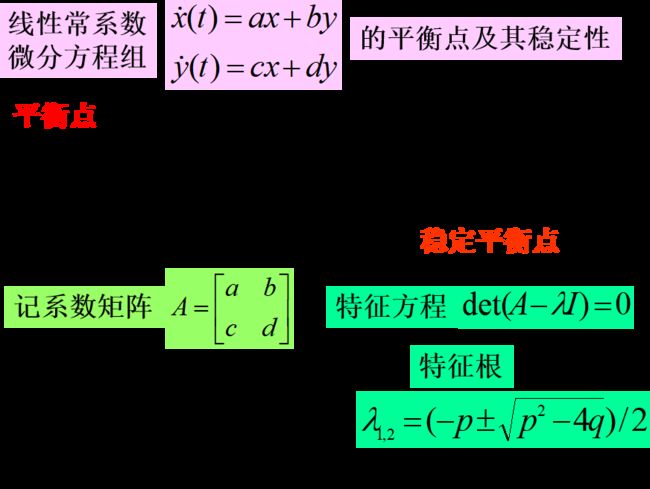
线性常系数微分方程组
模型的定性解释
种群的相互竞争
模型假设
模型建立
模型分析
线性常系数微分方程组
判断稳定性的方法——直接法
平衡点稳定性分析
种群竞争模型的平衡点及稳定性
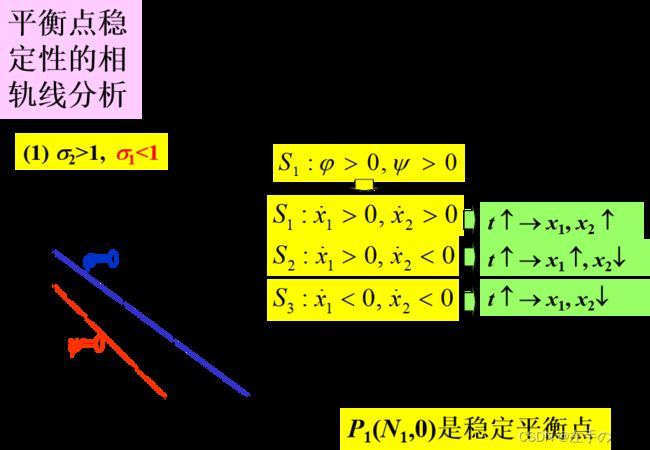
平衡点稳定性的相轨线分析
matlab验证
种群的相互依存
模型假设
模型建立
种群依存模型的平衡点及稳定性
平衡点P2稳定性的相轨线
matlab验证
食饵-捕食者模型(种群的弱肉强食)
食饵-捕食者模型(Volterra)
Volterra模型的平衡点及其稳定性
MATLAB求微分方程数值解
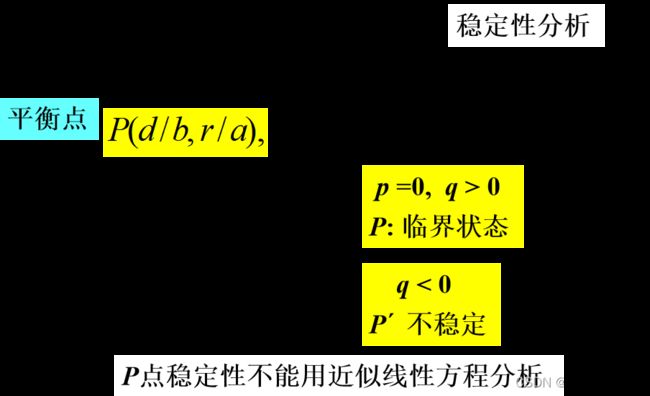
用相轨线分析P(d/b, r/a)点稳定性
模型解释
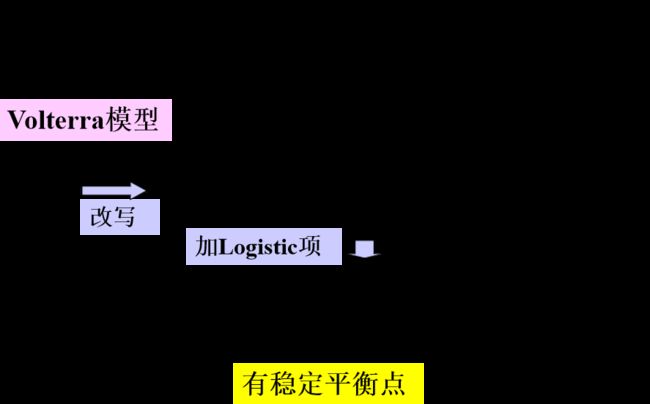
食饵-捕食者模型(Volterra)的缺点与改进
matlab验证
两种群模型的几种形式
差分形式的阻滞增长模型
模型分析
离散形式阻滞增长模型的平衡点及其稳定性
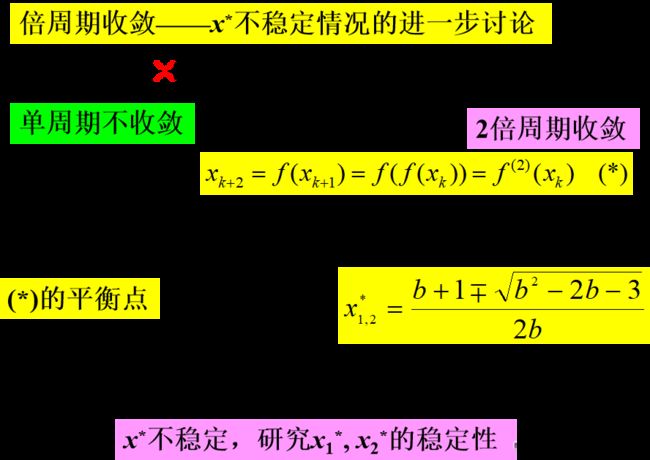
倍周期收敛——x*不稳定情况的进一步讨论
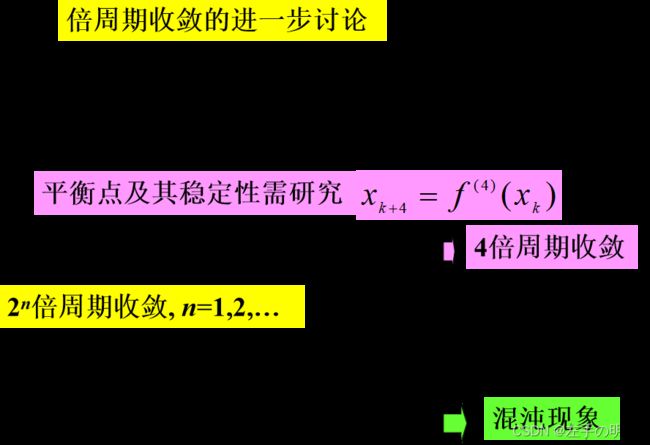
混沌现象
matlab验证
捕鱼业的持续收获
背景
- 再生资源(渔业、林业等)与 非再生资源(矿业等)
- 再生资源应适度开发——在持续稳产前提下实现最大产量或最佳效益
问题及分析
- 在捕捞量稳定的条件下,如何控制捕捞使产量最大或效益最佳?
- 如果使捕捞量等于自然增长量,渔场鱼量将保持不变,则捕捞量稳定
产量模型
x(t) ~ 渔场鱼量
假设
- 无捕捞时鱼的自然增长服从 Logistic规律.
r~固有增长率, N~最大鱼量
- 单位时间捕捞量与渔场鱼量成正比.
建模
有捕捞情况下渔场鱼量满足
不需要求解x(t),只需知道x(t)稳定的条件.
一阶微分方程的平衡点及其稳定性
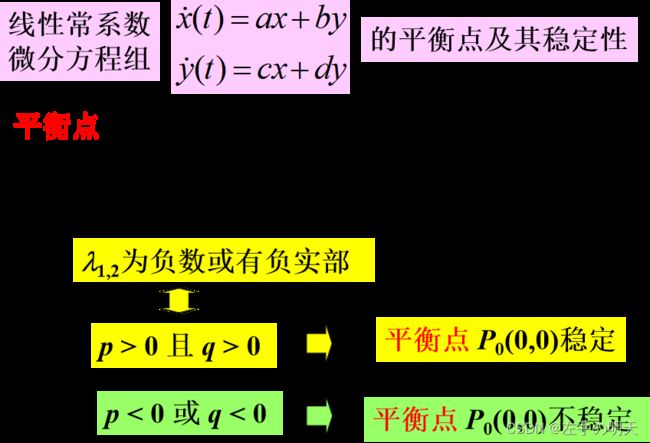
设x(t)是方程的解,若从x0 某邻域的任一初值出发,都有 称x0是方程(1)的稳定平衡点.
称x0是方程(1)的稳定平衡点.
直接法
图解法
在捕捞量稳定的条件下,控制捕捞强度使产量最大.
效益模型
在捕捞量稳定的条件下,控制捕捞强度使效益最大.
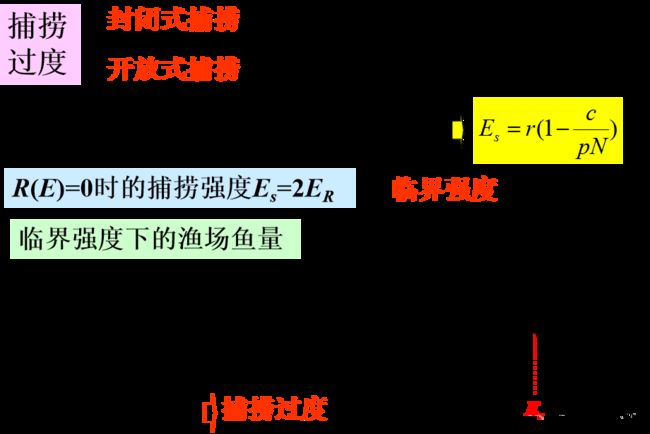
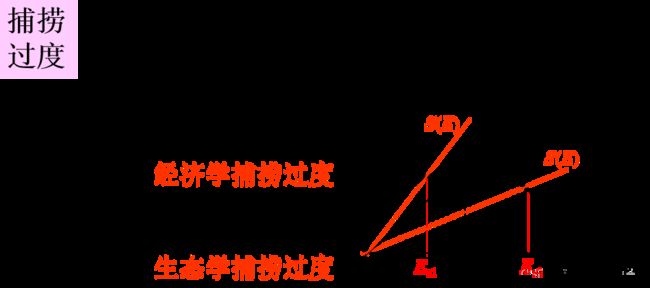
捕捞过度
捕鱼业的持续收获
在自然增长和捕捞情况的合理假设下建模.
用平衡点稳定性分析确定渔场鱼量稳定条件,讨论产量、效益和捕捞过度3个模型.
matlab验证
捕鱼业的持续收获 ——产量模型
产量模型:
其中,
- x(t)为t时刻渔场中的鱼量。
- r是固有增长率。
- N是环境容许的最大鱼量。
- E是捕捞强度,即单位时间捕捞率。
clear; clc;
%无捕捞条件下单位时间的增长量:f(x)=rx(1-x/N)
%捕捞条件下单位时间的捕捞量:h(x)=Ex
%F(x)=f(x)-h(x)=rx(1-x/N)-Ex
%捕捞情况下渔场鱼量满足的方程:x'(t)=F(x)
%满足F(x)=0的点x为方程的平衡点
%求方程的平衡点
syms r x N E; %定义符号变量
Fx=r*x*(1-x/N)-E*x; %创建符号表达式
x=solve(Fx,x) %求解F(x)=0(求根)
%得到两个平衡点,记为:
% x0= -N*(-r+E)/r , x1= 0
x0=x(2);
x1=x(1);%符号变量x的结构类型成为<2×1sym>
%求F(x)的微分F'(x)
syms x; %定义符号变量x的结构类型为<1×1sym>
dF=diff(Fx,'x'); %求导
dF=simple(dF) %简化符号表达式
%得 F'(x)= r-2*r*x/N-E
%求F'(x0)并简化
dFx0=subs(dF,x,x0); %将x=x0代入符号表达式dF
dFx0=simple(dFx0)
%得 F' (x0)= -r+E
%求F' (x1)
dFx1=subs(dF,x,x1)
%得 F' (x1)= r-E
%若 E0,故x0点稳定,x1点不稳定(根据平衡点稳定性的准则);
%若 E>r,则结果正好相反。
%在渔场鱼量稳定在x0的前提下(E 军备竞赛
目的
- 描述双方(国家或国家集团)军备竞赛过程.
- 解释(预测)双方军备竞赛的结局.
假设
- 1)由于相互不信任,一方军备越大,另一 方军备增加越快;
- 2)由于经济实力限制,一方军备越大,对自己军备增长的制约越大;
- 3)由于相互敌视或领土争端,每一方都存在增加军备的潜力.
进一步假设
1)2)的作用为线性;3)的作用为常数.
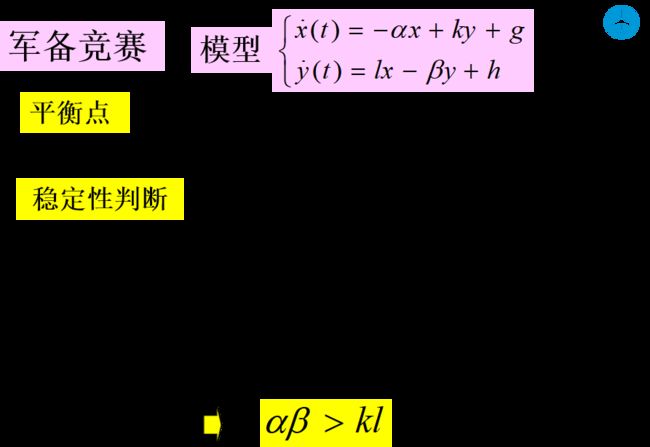
建模
线性常系数微分方程组
模型的定性解释
种群的相互竞争
一个自然环境中有两个种群生存,它们之间的关系:相互竞争;相互依存;弱肉强食。
当两个种群为争夺同一食物来源和生存空间相互竞争时,常见的结局是,竞争力弱的灭绝,竞争力强的达到环境容许的最大容量。
建立数学模型描述两个种群相互竞争的过程,分析产生这种结局的条件。
模型假设
模型建立
模型分析
线性常系数微分方程组
判断稳定性的方法——直接法
平衡点稳定性分析
种群竞争模型的平衡点及稳定性
平衡点稳定性的相轨线分析
matlab验证
模型:
![]()
其中,
- x1(t), x2(t)分别是甲乙两个种群的数量。
- r1, r2是它们的固有增长率。
- N1, N2是它们的最大容量。
- σ1:单位数量乙(相对N2)消耗的供养甲的食物量为单位数量甲(相对N1)消耗的供养甲的食物量的σ1倍。对σ2可作相应解释。
clear; clc;
%甲乙两个种群满足的增长方程:
% x1'(t)=f(x1,x2)=r1*x1*(1-x1/N1-k1*x2/N2)
% x2'(t)=g(x1,x2)=r2*x2*(1-k2*x1/N1-x2/N2)
%求方程的平衡点,即解代数方程组)
% f(x1,x2)=0
% g(x1,x2)=0
%编写出该程序段。
syms x1 x2 r1 r2 N1 N2 k1 k2;
f=r1*x1*(1-x1/N1-k1*x2/N2);
g=r2*x2*(1-k2*x1/N1-x2/N2);
[x1,x2]=solve(f,g,x1,x2);
P=[x1([2,3,4,1]),x2([2,3,4,1])];
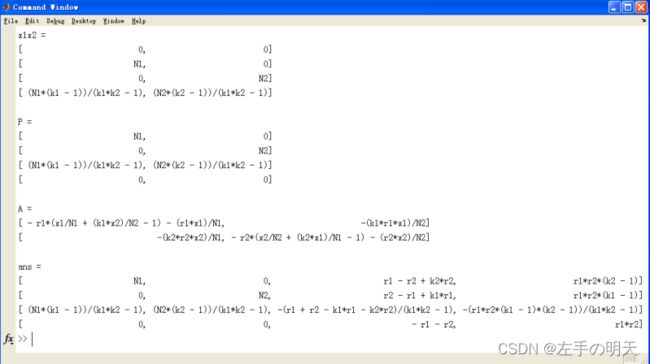
x1x2=[x1,x2] %显示结果
disp(' '); P
%调整位置后的4个平衡点:
% P(1,:)=P1(N1,0)
% P(2,:)=P2(0,N2)
% P(3,:)=P3(N1*(-1+k1)/(-1+k2*k1),N2*(-1+k2)/(-1+k2*k1))
% P(4,:)=P4(0,0)
%平衡点位于第一象限才有意义,故要求P3:k1, k2同小于1,或同大于1。
%判断平衡点的稳定性
syms x1 x2; %重新定义
fx1=diff(f,'x1'); fx2=diff(f,'x2');
gx1=diff(g,'x1'); gx2=diff(g,'x2');
disp(' '); A=[fx1,fx2;gx1,gx2] %显示结果
p=subs(-(fx1+gx2),{x1,x2},{P(:,1),P(:,2)}); %替换
p=simple(p);%简化符号表达式p
q=subs(det(A),{x1,x2},{P(:,1),P(:,2)});
q=simple(q);
disp(' '); [P p q] %显示结果种群的相互依存
自然界中处于同一环境中的两个种群相互依存而共生.
- 受粉的植物与授粉的昆虫.
以植物花粉为食物的昆虫不能离开植物独立生存,而昆虫的授粉又可以提高植物的增长率.
- 人类与人工饲养的牲畜.
种群甲可以独自生存,种群乙不能独自生存;甲乙一起生存时相互提供食物、促进增长.
甲乙两种群的相互依存有三种形式
- 1) 甲可以独自生存,乙不能独自生存;甲乙一起生存时相互提供食物、促进增长。
- 2) 甲乙均可以独自生存;甲乙一起生存 时相互提供食物、促进增长。
- 3) 甲乙均不能独自生存;甲乙一起生存时相互提供食物、促进增长。
模型假设
- 甲可以独自生存,数量变化服从Logistic规律; 甲乙一起生存时乙为甲提供食物、促进增长。
- 乙不能独自生存;甲乙一起生存时甲为乙提供食物、促进增长;乙的增长又受到本身的阻滞作用 (服从Logistic规律)。
模型建立
种群依存模型的平衡点及稳定性
平衡点P2稳定性的相轨线
matlab验证
模型:
其中,
- x1(t), x2(t)分别是甲乙两个种群的数量。
- r1, r2是它们的固有增长率。
- N1, N2是它们的最大容量。
- σ1:单位数量乙(相对N2)提供的供养甲的食物量为单位数量甲(相对N1)消耗的供养甲的食物量的σ1倍。对σ2可作相应解释。
clear; clc;
syms x1 x2 r1 r2 N1 N2 k1 k2;
f=r1*x1*(1-x1/N1+k1*x2/N2);
g=r2*x2*(-1+k2*x1/N1-x2/N2);
[x1,x2]=solve(f,g);
P=[x1([2,4,1,3]),x2([2,4,1,3])];
syms x1 x2; %重新定义
fx1=diff(f,'x1'); fx2=diff(f,'x2');
gx1=diff(g,'x1'); gx2=diff(g,'x2');
A=[fx1,fx2;gx1,gx2];
p=subs(-(fx1+gx2),{x1,x2},{P(:,1),P(:,2)}); %替换
p=simple(p);%简化符号表达式p
q=subs(det(A),{x1,x2},{P(:,1),P(:,2)});
q=simple(q);
[P p q] %显示结果食饵-捕食者模型(种群的弱肉强食)
种群甲靠丰富的天然资源生存,种群乙靠 捕食甲为生,形成食饵-捕食者系统,如 食用鱼和鲨鱼,美洲兔和山猫,害虫和益虫.
模型的历史背景——一次世界大战期间地中海 渔业的捕捞量下降(食用鱼和鲨鱼同时捕捞), 但是其中鲨鱼的比例却增加,为什么?
食饵-捕食者模型(Volterra)
Volterra模型的平衡点及其稳定性
MATLAB求微分方程数值解
用相轨线分析P(d/b, r/a)点稳定性
模型解释
食饵-捕食者模型(Volterra)的缺点与改进
matlab验证
函数M文件:
function xdot=shier(t,x)
r=1; d=0.5; a=0.1 ; b=0.02 ;
xdot=[(r-a*x(2)).*x(1); (-d+b*x(1)).*x(2)];命令M文件:
ts=0 :0.1 :15;
x0=[25, 2];
[t,x]=ode45('shier',ts,x0); [t,x],
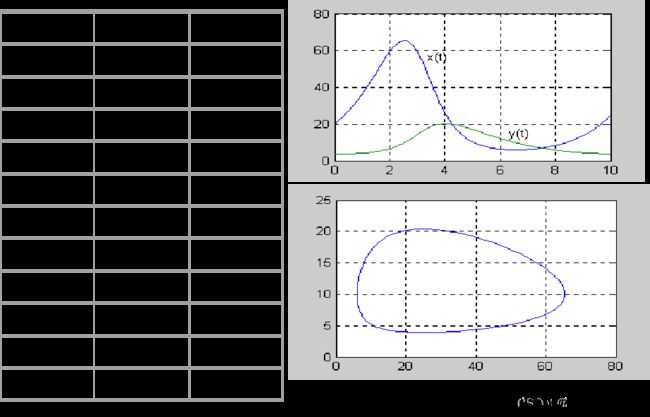
plot(t,x), grid, gtext('x(t)'), gtext('y(t)'), %运行中在图上标注
pause,
plot(x(:,1),x(:,2)), grid, x(t), y(t)图形:
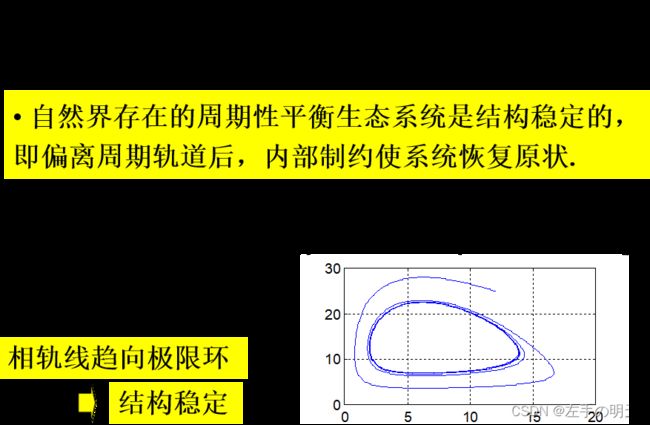
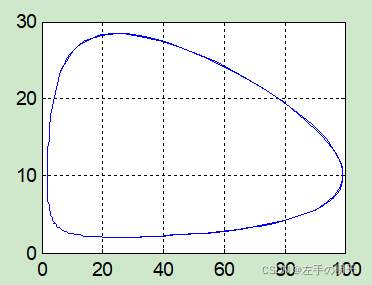
相轨线y(x)图形:
两种群模型的几种形式
差分形式的阻滞增长模型
模型分析
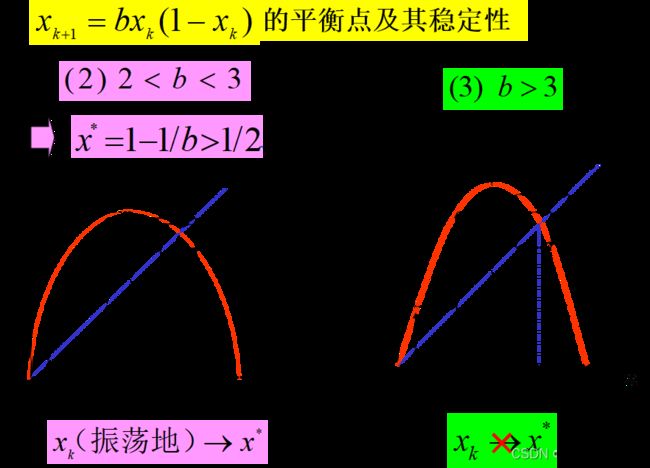
离散形式阻滞增长模型的平衡点及其稳定性
倍周期收敛——x*不稳定情况的进一步讨论
混沌现象
matlab验证
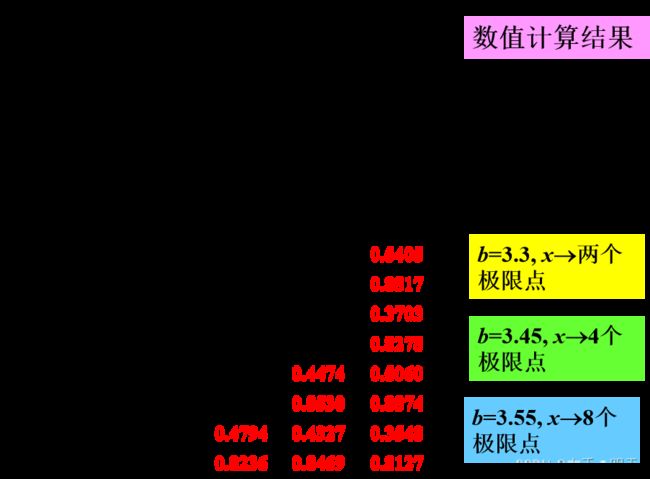
取x0=0.2,分别取b = 1.7, 2.6, 3.3, 3.45, 3.55, 3.57,对方程
计算出x1 ~ x100的值,显示x81 ~ x100的值。观察收敛与否。
clc; clear all; format compact;
b=[1.7,2.6,3.3,3.45,3.55,3.57];
x=zeros(100,length(b));
x0=0.2; %初值
x(1,:)=b*x0*(1-x0);
for k=1:99
x(k+1,:)=b.*x(k,:).*(1-x(k,:));
end
K=(81:100)’; %将取81~100行
disp(num2str([NaN,b; K,x(K,:)],4));%取4位有效数字,NaN表示不是数值
clear; clc; close all;
f=@(x,b)b.*x.*(1-x); %定义f是函数的句柄,函数b*x*(1-x)含两个变量x,b
b=[1.7,2.6,3.3,3.45,3.55,3.57];
x=ones(101,length(b));
x(1,:)=0.2;
for k=1:100
x(k+1,:)=f(x(k,:),b);
end
for n=1:length(b)
figure(n);%指定图形窗口figure n
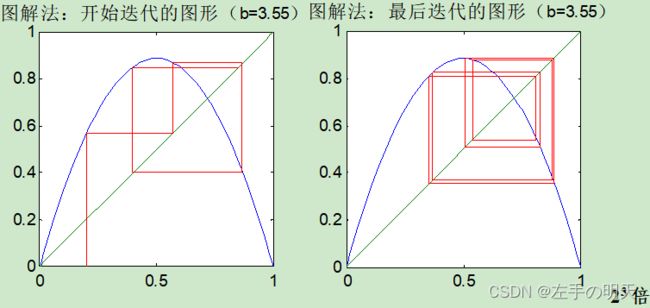
subplot(1,2,1);%开始迭代的图形
fplot(@(x)[f(x,b(n)),x],[0 1 0 1]);%x是自变量,画曲线y=bx(1-x)和直线y=x
axis square; hold on;
x0=x(1,n); y0=0; %画迭代轨迹线
for k=2:5
x1=x(k,n); y1=x(k,n);
plot([x0+i*y0, x0+i*y1, x1+i*y1], 'r');%实部为横坐标,虚部为纵坐标
x0=x1; y0=y1;
end
title(['图解法:开始迭代的图形(b=' num2str(b(n)) ')']);
hold off;
subplot(1,2,2); %最后迭代的图形
fplot(@(x)[f(x,b(n)),x],[0 1 0 1]);
axis square; hold on;
xy(1:2:41)=x(81:101,n)+i*x(81:101,n);%尽量不用循环
xy(2:2:40)=x(81:100,n)+i*x(82:101,n);
plot(xy,'r');
title(['图解法:最后迭代的图形(b=' num2str(b(n)) ')']);
hold off;
end运行程序并给出结果(对应不同的b值)
![]()