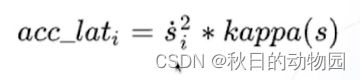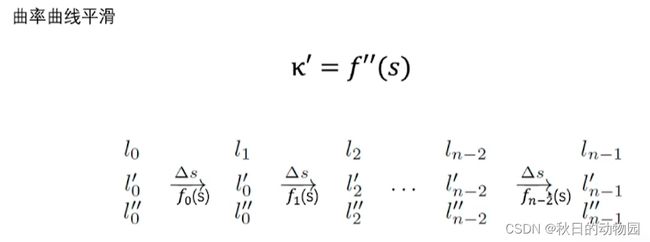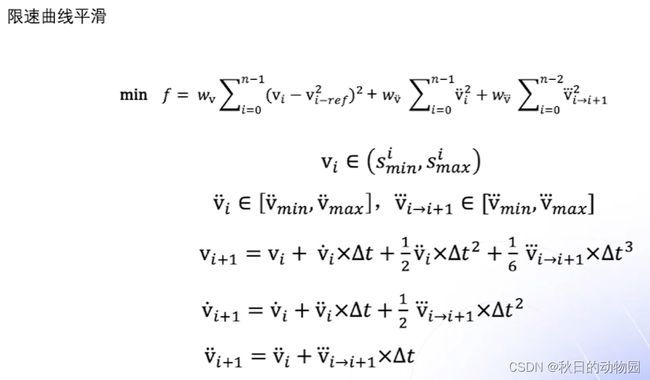4.速度规划算法解析及实现

星火计划2.0基础课：https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课：https://apollo.baidu.com/community/online-course/12

速度规划的s是沿着路径方向的位移，路径规划的s是沿着参考线方向的位移。

各车辆状态的st图：

现在来看Apollo算法中整体的流程：

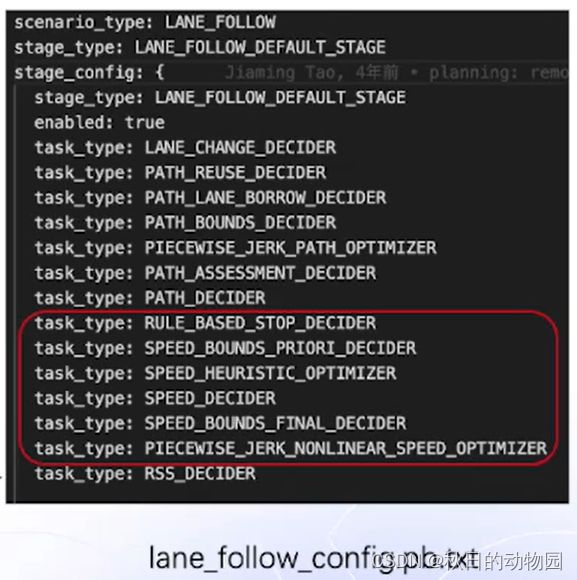
其文件lane_follow_config.pb.txt为主路场景的任务配置文件，主路场景的后几个task都是跟速度规划相关的任务。

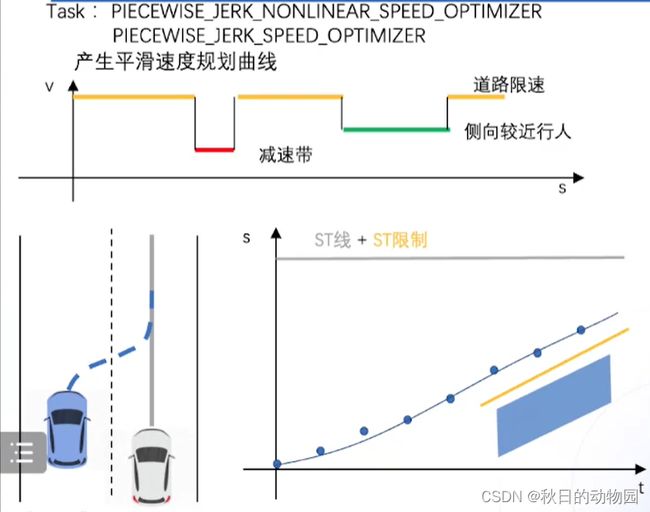
第一个SPEED_BOUNDS_PRIORI_DECIDER,主要是为动态规划，速度规划算法确定st曲线的边界，比如预测旁边车道的插入自车道的轨迹，蓝色出现的时间(平行四边形)，即为障碍车切入主车路径的时间，此时主车既可以加速超过去，又可以减速绕行。这样障碍物就将可行驶的曲率划分成两个不连续的空间，所以可行域显然是一个非凸的空间，也就不能应用凸优化的方法进行求解。所以首先用动态规划的方法进行搜索，确定是对障碍物进行绕行还是超车。

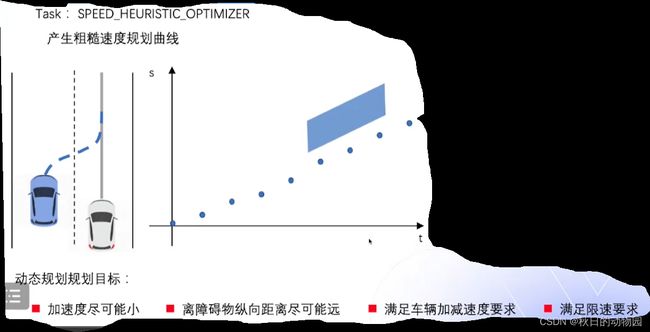
动态规划会进行迭代求解一条没有碰撞的，满足约束的最优的一条速度规划的曲线，动态规划目标函数里会考虑加速度要尽可能地小，离障碍物尽可能远，要满足自车最大的加速和减速要求，为了满足搜索效率，动态规划的点会比较稀疏。

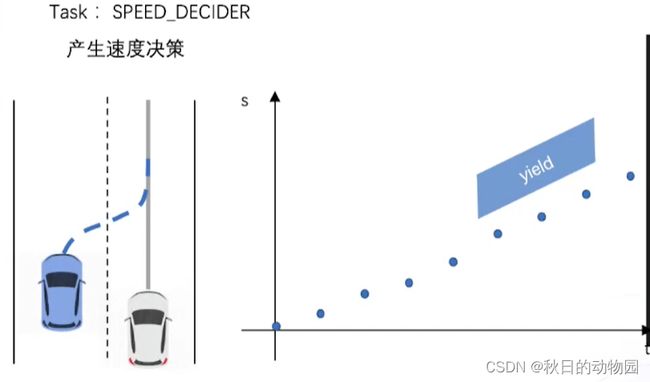
该决策是确定对障碍物是超车还是绕行的决策。

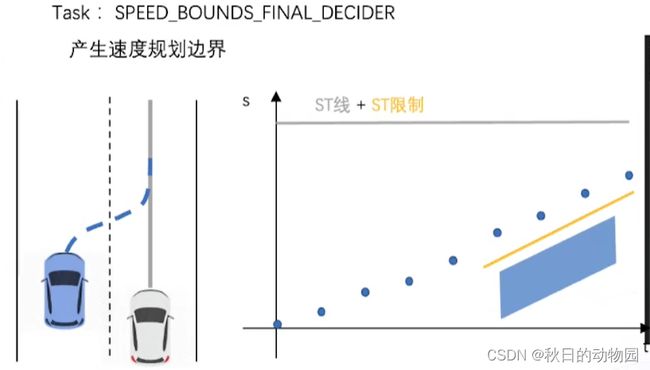
此任务是确定障碍物最终的边界，比如之前设定的障碍物决策中产生了一个对障碍物让行的决策。

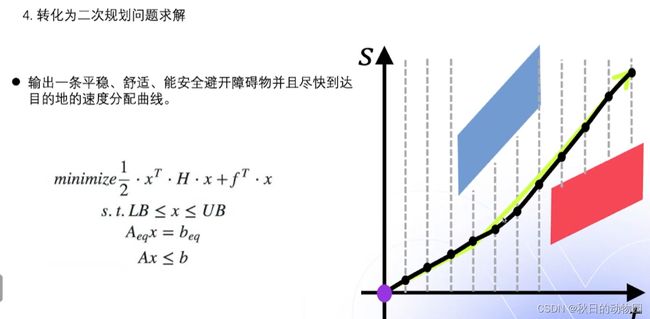
接下来是速度规划的优化算法，根据ST图的可行驶区域优化出一条平滑的速度曲线，该曲线要满足一阶导和二阶导要平滑，即速度和加速度变化要尽可能平稳，另外还要满足道路的限速的要求，以及车辆运动学约束。

这里速度规划有两个优化器，一个是基于二次规划的速度优化器，另一个是基于非线性规划的速度优化器。

非线性优化器求解主要是考虑路径曲率对速度规划的影响，因为曲率约束是一个非线性的函数。在配置文件中这两个优化器二选一即可。

然后最后将路径规划的sl曲线和st曲线合成一条完整的轨迹，这里轨迹就是以时间T为间隔生成一系列的轨迹点。这一系列点就作为planning最后的输出。

接下来介绍基于动态规划的速度规划:

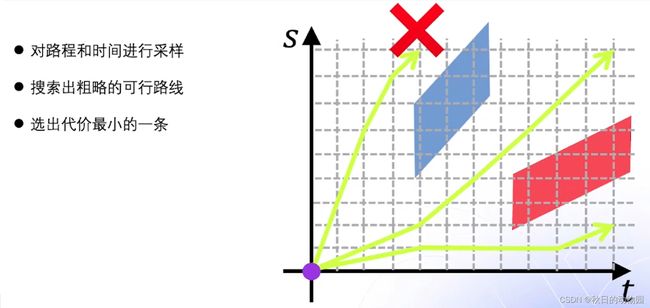
在apollo的速度规划中，动态规划主要是用来做速度决策的判定，动态规划作为一种采样搜索算法，首先是对路径s和时间t进行采样，然后迭代搜索出一个粗糙的可行曲线，接着选择出代价最小的一个。

速度规划是基于st进行规划，所以第一步首先是对st图进行采样，作为一个栅格图，在t方向上采取固定间隔进行采样，apollo默认设置1s进行采样，对于s方向进行先密后疏的采样间隔进行采样。

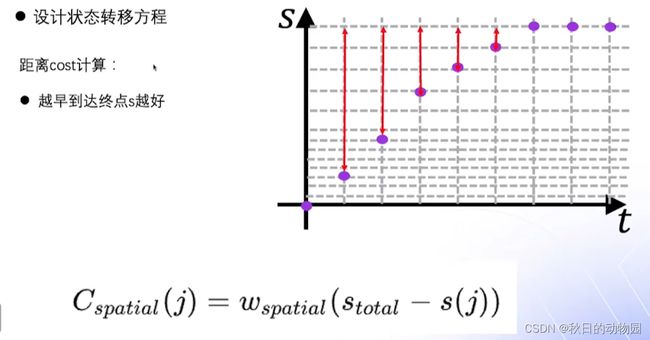
接下来是动态规划的状态转移方程的设计，希望和障碍物满足一定的安全的距离，另外要求和障碍物不能发生碰撞，可以得到代价函数：

其中i代表时间t，j代表位移s。如果点在障碍物范围内，其代价就设置为无穷，另外还设置了一个跟车和超车的安全距离，如果在安全距离以外，其代价就设为0。如果点在障碍物和安全距离之间，就以超出安全距离的部分的cost进行计算。

接下来是一个距离cost的计算:

其拉动曲线尽可能的到达终点位置，其取得终点s和当前s的差值乘以一个损失权重。

上述都是节点的代价，除了节点以外，还有节点之间转移的代价(边的代价)

状态转移的代价也分为三部分：

状态转移的速度代价，加速度代价，加加速度的代价。从目标函数也可以看出来，速度是输入包含两个点，从i到i+1，从j到j+k点的代价(边的代价)，速度计算就是两个节点的位移差除以时间间隔，如果速度小于0，说明倒车，这样的轨迹是不可行的，所以将cost设为无穷大，这里还定义了超速的指标:超出的速度减去限速值，再除以限速值。代价函数中设置了超速代价，超速部分要乘以超速的权重，如果速度低于限速的话还要有低速的惩罚。Apollo中超速惩罚和低速惩罚是不一样的，超速惩罚是远大于低速惩罚的，超速惩罚设置为1000，低速惩罚设置为10.

对于加速度cost计算就是用前一个节点的速度减去后一个节点速度除以时间间隔t。加速度的代价函数设计为，如果加速度超过了最大设定加速度或最大减速度，这种轨迹是不可行的，其代价设置为无穷大(因为运动学限制)。如果所规划的加速度在最大加速度和最小加速度之间，apollo设计了一个指数的代价函数，当加速度为正时，设置一个正加速度的惩罚，加速度为负时设置一个负加速度的惩罚，代价函数如图：

加速度越接近于0，其代价越小。越接近于边界其代价越大。主要是期望一个较小的加速度或者减速度进行规划，保证行驶的舒适性。

对于加加速度的计算主要通过四个点s方向的坐标进行计算，如果jerk超出加加速度设定的边界，此时的cost就

是无穷大，否则jerk使用二次方的代价函数，即期望加加速度越小越好。

则总的状态转移方程如下：

其包括障碍物的代价，距离的代价，边的代价，每次迭代搜索的时候会去进行更新当前节点的代价。迭代的范围是通过当前的节点的速度和当前节点的s和t以及规划的车辆最佳的加速度和车辆当前的速度拓展当前能行驶的节点。 比如从s(i,j)到s(i+1,j+k),可以拓展在速度范围内的能到达的一些节点，然后进行节点的更新，如果cost更小，就把它的cost更新为新的cost值和新的前驱节点，通过求解最后一列s的最小的cost作为最终解，通过回溯可以得到所有的s，t点，就得到了动态规划的st曲线。

下面讲解基于二次规划的速度规划：

动态规划生成的st曲线因为点数比较少，比较粗糙后面还需要用优化算法对动态规划产生一个凸空间的轨迹进行进一步的平滑。

基于二次规划的速度规划算法和基于二次规划的路径规划算法是比较类似的，不同点是速度规划是在st域内进行规划，主要有三步：

最后转化为二次型的格式。

首先是确定优化变量：

通过对t选取等间隔时间点的s，s的一阶导，s的二阶导，此时加加速度就可以通过任意两个点的加速度之差除以时间间隔求得。接下来设计目标函数，即明确需要努力满足的一个目标：

其中ws是位置的权重，wv是参考速度的权重，pi是根据决策制定的速度分配确定的i时刻的曲率确定的权重，wa是一个加速度权重，wj是一个加加速度的权重。

接下来设计需要满足的约束条件：

第一点需要设计车不能和障碍物有碰撞，即s在之前确定的st边界范围内，第二点是车的加速度，加加速度不能超过运动学的限制，第三点是要满足基本的物理学原理，最后为起始点的约束，即起始点的位置速度加速度要满足规划起点的位置速度加速度。

最后将上述公式转化为二次型问题，通过代入osqp求解器进行求解就可以输出一条平稳、舒适、可以安全避开障碍物的一条速度分配的曲线。

这里osqp求解器在上一节路径规划课程中也讲过了。

最后为了使得限速更加精细，apollo还提出了一种基于非线性规划的速度规划算法：

在讲解非线性规划算法之前，先分析一下二次规划的速度规划算法的问题。

二次规划的曲率规划的惩罚pi是曲率关于时间t的函数，但实际上路径的曲率是和s相关的。

二次规划的速度规划通过对动态规划粗糙的st曲线，将关于s的区域惩罚转化为关于t的区域的惩罚，此时如果平滑后的曲线和原来动态规划的st曲线相差不大的时候，其惩罚位置是正确的，如果平滑后的曲线和原始的动态规划的st曲线相差较大，实际的惩罚区间就和设定的不一样。

比如上图中应该惩罚的区间为橙色区间，而二次规划算法实际对于曲率惩罚的区域是在绿色的区域。还有比如地图的限速约束也是和s相关的，所以这样的问题就在于，限速或者曲率的函数是关于s的函数，而s又是待求的量(优化量)，就无法对目标函数施加速度约束或者曲率的约束，只能通过动态规划的st曲线进行转化，转化成t的函数再施加约束，但这样就会导致二次规划算法的st曲线的速度约束不精确的问题。

apollo这里设计了一种基于非线性规划的优化算法，最后通过ipout求解器进行求解来解决该问题。

非线性规划算法和其他优化算法的步骤都是一样的，首先确定优化变量：

优化变量的采样方法是和二次规划是一样的，采用等间隔的时间采样，包括s，s的一阶导，s的二阶导，另外还有两组关于s的松弛变量，起作用主要是为了避免求解失败，也作为一个优化变量进行规划。

然后定义非线性规划的目标函数：

其和二次规划的目标函数基本一致:使规划曲线尽可能接近参考线的代价、接近巡航速度行驶的代价、加速度加加速度尽可能小的代价、这里又额外增加了一个横向加速度尽可能小的代价以及松弛变量尽可能小的代价。因为横向加速度也是影响舒适度的一个约束。

其计算就是v方/R

由于曲率是关于s的关系式，这里还要对该曲率进行进一步的平滑 ，因为对于非线性规划求解器，无论是目标函数还是约束都是要求函数能够二阶可导：

那么这个曲率之前是怎么来的呢？

上节课讲到了，规划路径是通过分段多项式的二次规划算法求得的，每一段的s和l都是保持的三阶导为定值的一个多项式的曲线关系，它可以保证sl是二阶可导，但是求得s的曲率实际上并不是二阶可导的，所以这里需要对曲率曲线重新做一个拟合，生成s关于曲率二阶可导的一个关系式。这里apollo同样采用分段多项式的方法获得s关于曲率kappa的关系式。首先对s进行采样，然后求解s关于曲率的分段多项式的关系式。

这里曲率平滑也是使用二次规划算法。和路径和速度的二次规划算法比较类似。分别采用曲率的一阶导，二阶导，三阶导作为目标函数。最后求解出平滑的曲率的曲线

然后讲解非线性规划算法的约束定义：

首先规划的速度要一直往前走，即后一个点的位移要大于前一个点的位移，其次加加速度不能超过定义的极限值，同时还要满足限速要求。

现在来看上述的限速函数：

此时得出的曲线既不连续也不可导，所以要对限速曲线进行平滑。

限速曲线的平滑apollo还是用的分段多项式曲线平滑，用二次规划进行求解。

其约束为：

为了避免求解失败，在二次规划中对位置的硬约束，在非线性规划里转换成对位置的软约束。

因为障碍物的st图是根据障碍物的预测轨迹投影来的，既然是预测就有预测不准的情况，如果是硬约束，在一些极端情况下就会导致求解失败(求解器没有办法求出可行解)。

非线性规划，目标函数和约束就不再限制于二次型了，所以另外加了一些对于位置的软约束，即允许超出s上下边界范围，但是超出会在目标函数里对超出的松弛量有一个比较大的惩罚。另外还要满足一些基本的物理学原理的约束。

最后将问题代入ipopt这个非线性规划求解器去进行求解。这里要求目标函数和约束函数都是二阶可导的。

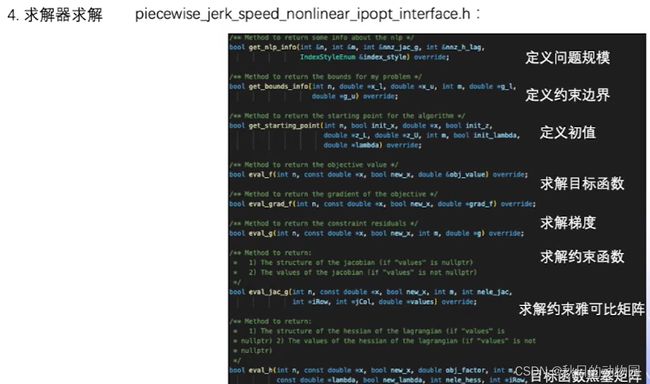
接下来是求解器求解过程：

ipopt算法需要去实现以上几个函数，求解器会通过调用这几个函数来了解我们对于问题的定义。

对于速度规划问题，如何定义初始解？

apollo还是用分段的二次规划求解方法，得到一条符合约束的速度平滑曲线作为非线性规划的初值。

为了知道目标函数的方向，还要求解梯度。

梯度就是函数对于其各个变量的偏导数。

因为对曲率函数做了平滑即满足二阶可导的性质，所以也可以得到曲率的导函数。

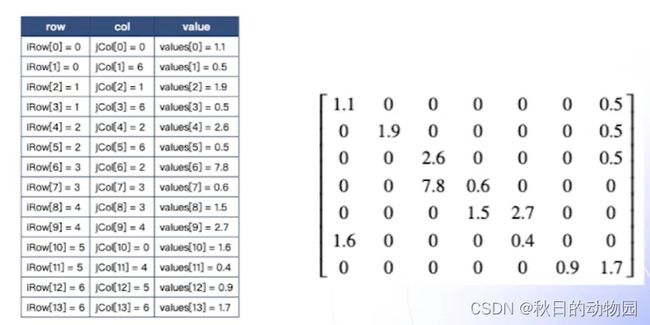
雅可比矩阵就是向量函数的梯度所组成的区间。其行向量是优化变量，纵向量是约束函数。

因为有些偏导数求解完为0，为了增加非线性规划求解器的效率，这里只要给出非0元素的位置和值就可以了。

约束函数有如下几个：

(黑塞矩阵就是hessian矩阵)

对函数进行二阶偏导所得的矩阵，该函数为：

其是最优化问题中将带约束的优化问题转化成无约束优化问题的构造的函数，其中f为目标函数，g为约束函数，λ为拉格朗日的乘子。

ipopt的黑塞矩阵就是对于拉格朗日函数求二阶偏导：

目标函数求二阶偏导(黑塞矩阵中的非0项)：

有兴趣可以和代码对应一下。

最后是求解器求解完成获得的最优解：