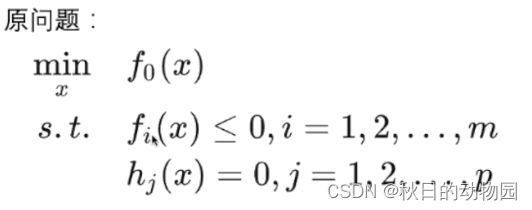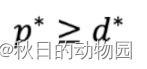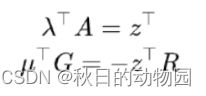5.开放空间规划算法解析及实现

星火计划2.0基础课：https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课：https://apollo.baidu.com/community/online-course/12

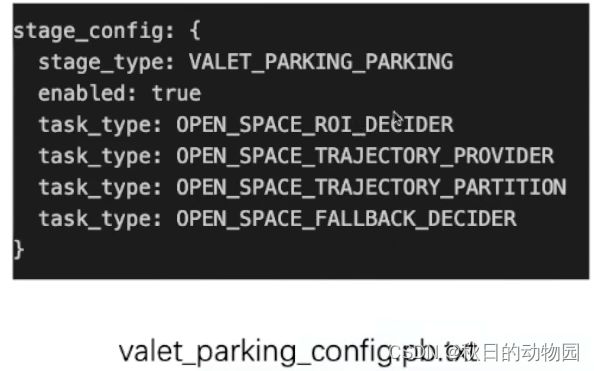
apollo的planning中处理的绝大多数场景都是在城市结构化道路的路径规划。需要从高精地图的车道线中产生一条参考线，然后基于参考线再进行规划，但是对于一些没有参考线的非结构化场景，比如载客泊车，就需要在开放空间进行路径规划。开放空间算法主要应用在一些泊车场景或靠边停车场景，对于泊车场景的开放空间算法，其任务主要集中在下面的配置文件中：

泊车场景如上，一共有四个任务：

确定可行驶区域：

可行驶区域主要是根据道路的边界和泊车位的边界来确定。

另外如果可行驶区域中存在障碍物，则需要把障碍物的边界考虑进来。

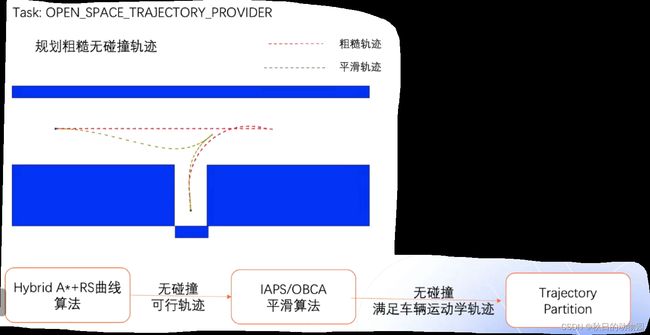
规划无碰撞轨迹：

该任务主要分为两步：第一步是通过混合A*算法和RS曲线规划出一条粗糙的轨迹，主要是求出一条没有碰撞的参考解，因为混合A*和RS曲线规划的路径会存在一些曲率的突变，即不满足车辆的运动学约束要求的，所以第二步还要采用IAPS和OABC算法，对轨迹进行进一步的平滑，使得轨迹满足控制的需求。

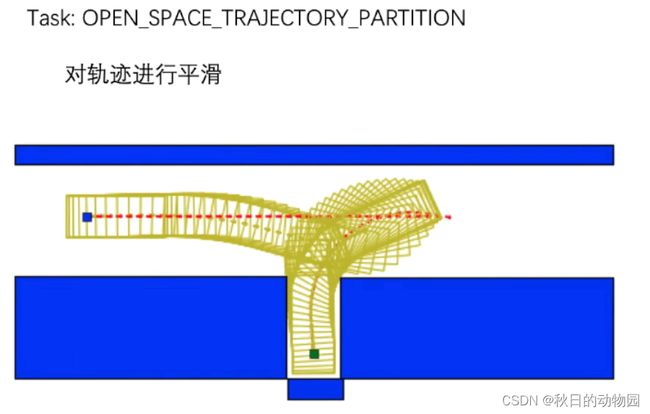
接下来是：

该任务是根据轨迹是前进的轨迹还是倒车的轨迹将轨迹进行一个分割，根据自车的位置判断发送哪一条轨迹，以及是否需要切换轨迹。

最后的任务是检查规划的轨迹是否会和障碍物发生碰撞，如果碰撞了就会进入一个fallback状态，规划一条在碰撞位置停车的轨迹，然后再重新进行路径规划。

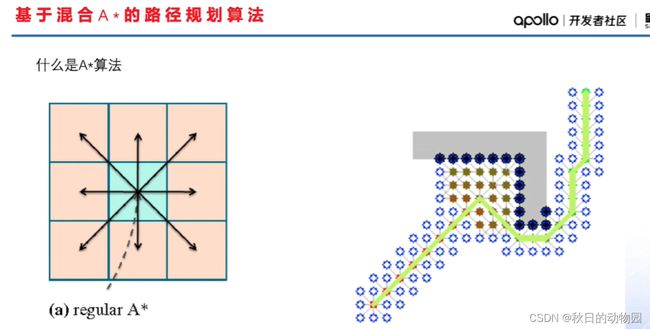
下面讲解混合A*算法：

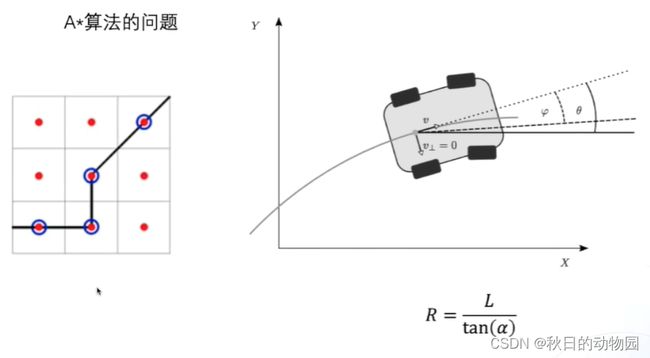
对于开放空间的路径规划，实际上是一个复杂度比较高的非凸问题，通过搜索算法实际上是一个效率比较高的方案，A*是在机器人领域应用比较多的一个基于搜索的路径规划算法。A*算法首先将可行驶空间进行一个栅格化，按固定距离间隔采样节点，从当前节点遍历前后左右，以及左前右前左后右后八个方向。通过迭代搜索的方法找到一条从起点到终点避开障碍物的一条路径。

A*算法的具体实现过程：

首先从起点开始遍历所有相邻的节点，由于设置了两个集合，一个是开放集合open_set,一个是闭集合close_set,开集合保存了所有等待遍历的节点，闭集合保存了所有已经遍历过的节点，每次首先是把当前节点(起始节点)放入闭集合中，在下次搜索中从开集合中选择cost最小的节点作为遍历节点，ccost的计算包含两部分:g(n)表示从节点到当前节点的一个代价，h(n)是一个启发函数，表示从当前节点n到终点的一个预估的cost。

可以用到达终点的直线距离作为一种启发函数，设计一个比较精准的启发函数也可以加快搜索的速度。

可以看出来A*算法产生的路径都是折线的，对于车辆来说，是没有办法走出这样的路径的，这样的路径也不满足车辆的运动学约束，根据车辆的运动学模型，实际车辆航向是和后轴中心的速度方向是一致的，所以可以把车辆的运动路径等效为后轴中心点的一段段不同转弯半径的弧线组成。通过前轮转角可以计算出后轴中心的转弯半径，可以考虑对前轮转角进行采样，不同的前轮转角会有不同的转弯半径，每次行驶一个固定的弧长，此时搜索出的路径如下图右侧所示，其是由不同半径的弧组成的：

这样的路径相对A*算法路径平滑了很多。

但是这样优化后带来的问题就是原来栅格点作为节点也就不再适用了，可以看到从弧线拓展的节点位置可能会坐落在棋盘格的各个位置，它们的方向(航向角)也是各不相同的，在A*算法中，通过x和y的坐标来判断节点是否遍历过的方法在这里也就不再适用了，即算法搜索状态空间从二维的x，y拓展到三维的x，y，θ，θ即当前处在该点车辆的航向角，所以节点除了定义x，y还要定义航向角θ的精度,以下是apollo中定义节点的数据格式：

其中x_grid,y_grid和phi_grid分别是节点x，y和phi的索引，即x，y方向的长度除以精度。通过三个索引组成的字符串是否相同，来确定其是否为同一节点，是否遍历过该节点。

因为搜索拓展路径节点动作是离散的，比如以固定的长度，不同的转弯半径进行节点的拓展，而状态空间其实是连续的，因此有可能永远也搜索不到终点的状态：

所以还需要进行节点的解析拓展——RS曲线:

提出了一种从起点到终点可以通过固定半径的圆弧和直线连接起来的方法，圆弧和直线的组合一共总结了48种(上图表格),而且证明了这样的最短路径一定是在这48种线型之中的，并且给出了每一种线型解析解的求解方法。

上表中，C代表圆弧，S代表直线，竖线代表前后有一次方向的变换。但该种方法是没有办法考虑障碍物的，所以应用到混合A*算法中，还要加上最后的一个碰撞检测，把和障碍物发生碰撞的所有路径过滤掉。

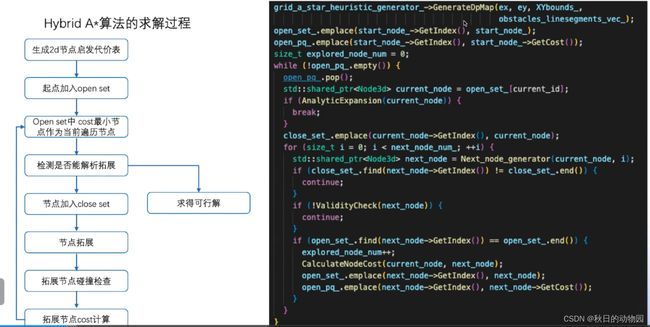
接下来以APOLLO中混合A*的代码为例，介绍混合A*算法的求解过程：

第一步：基于动态规划算法求解每个二维节点的代价值作为混合A*算法的启发函数(GenerateDpMap)，然后定义了两个集合，open_set和close_set以及优先队列open_pq_，保存开放集的节点。首先将起点放入开放集中，然后定义一个while循环，每次从优先队列中会弹出代价最小的一个节点，然后判断从当前节点状态到终点状态是否有无碰撞的一个RS曲线(AnalyticExpansion函数)，求出解析解，如果找不到解析解就可以直接退出循环了。然后将该节点加入闭合集，然后再从当前节点向外拓展搜索节点(Next_node_generator函数)，如果拓展的节点之前没有遍历过，也没有和障碍物发生过碰撞，就可以加入到开放集中，并计算节点的代价值(CalaulateNodeCost函数)。

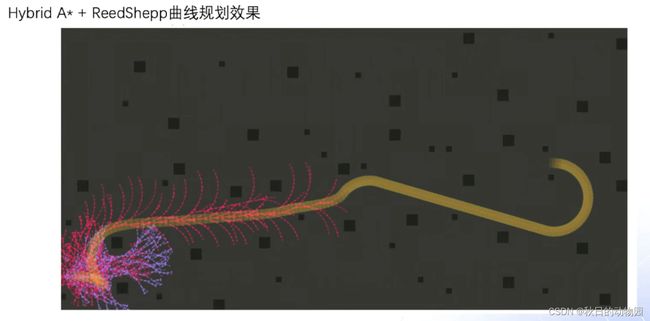
上图中黑色框表示可行驶区域中的障碍物，粉色点是通过混合A*搜索拓展得出的点，后半段没有通过混合A*的搜索，是通过RS曲线解析算出的一条路径，这样的路径虽然满足车辆运动学约束，但其中都是由弧和直线组成的，每个弧和直线衔接的位置都有一些曲率的突变，所以这样的路径还需要进一步进行平滑处理，来满足控制以及乘坐舒适性的要求。

接下来讲解第一个平滑算法:OBCA算法

OBCA算法不像混合A*那种基于搜索的规划算法，其是基于模型预测控制MPC建立的模型，然后用优化算法进行求解，OBCA算法可以加入一些障碍物的约束，不像求解解析解的RS曲线那样，虽然可以求出最优的解析解，但是没有办法考虑障碍物的碰撞约束。OBCA算法可以实现横纵向的联合规划，即可以同时考虑速度对路径的影响。且OBCA算法可以产生满足车辆运动学约束的轨迹，可以获取曲率连续变化的轨迹，而不像混合A*和RS曲线存在不同曲率的线段衔接到一起导致曲率突变的问题。

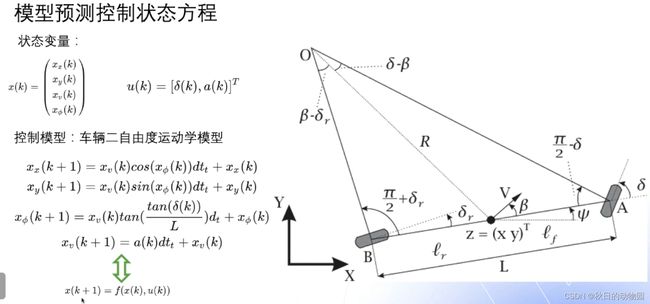
 因为MPC也是最后转换成一个优化问题，所以它和其他的优化问题一样，首先要设计目标函数，设计约束函数，因为MPC涉及预测的问题，要对未来问题进行优化求解，所以还需要再设计一下MPC的预测模型，也就是状态空间方程的建立：

首先定义状态变量，包含x，y坐标(笛卡尔坐标系)，车速，航向角；以及输入u(k)，包括主车的前轮转角以及加速度。

预测控制模型就是车辆的一个二自由度的运动模型，最后可以简化成k+1时刻的状态可以由k时刻的状态推导出来，在控制算法中需要的是u的第一个分量，但是在轨迹规划算法中一般需要整个预测时域的所有状态，即把所有状态作为最后输出的一个轨迹,x(k+1)=f(x(k),u(k)).

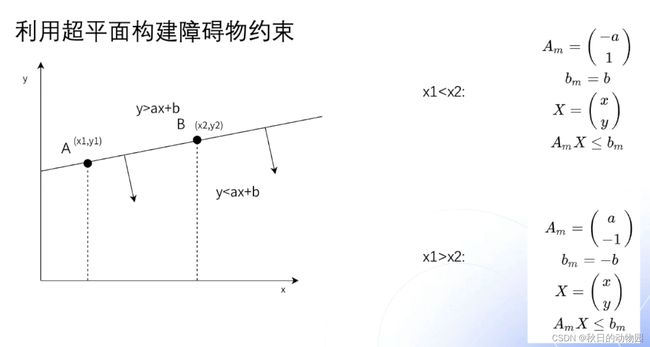
OBCA算法在规划时考虑了障碍物的约束，利用超平面来构建障碍物约束.三维超平面就是把空间分为两部分的面，二维超平面就是把面分成两部分的线：

代入X的坐标可以判断该点是在线段上方还是线段下方，通过求解A和B的坐标来求解得到约束函数的系数Am和bm.

障碍物可以用四条边或者多个边的约束表示出来，Am，bm由四个状态联立得出。

自车所占用的空间同样可以用超平面来表示：

E表示自车在原点位置所占用的空间，如果自车在第k时间所占用的空间可以利用状态变量x(k)加旋转矩阵R()和平移矩阵t()得到。

如果要保证自车和障碍物不发生碰撞就需要满足主车占用的空间和障碍物占用空间的交集为空集：

这里定义一个主车和障碍物的距离函数dist，即主车沿着任意的方向向量t平移和障碍物发生重合的范数最小的向量函数。大于d_min等价于上面一系列不等式的成立，其中λm和μm是拉格朗日乘数。

原问题就是求解自车在E(x)位置和障碍物Om的一个距离，定义e为自车占用空间E(x)中任意的一个点,o为障碍物m占用空间Om的任意一点，因此两个障碍物之间的距离就是欧几里得距离最短的eo两个点，为一个e到o的二范数，如果让该距离大于dmin,则有上式成立。这里将E(x(k))变为了R(x(k))e't(x(k)),这个e'表示在原点的自车空间中的一个点，通过旋转矩阵和平移矩阵，就可以得到e的位置(实际自车空间中的一点)。

由于范数中包含了两个优化变量，一个e’一个o，不好计算，所以引入新的优化变量w和等式约束。

然后就得到了如上图所示的新问题，即使w的二范数最小时候的e'和o的取值。在凸优化问题里对于这种有约束条件的极值问题通常是不好研究的，所以通常将有条件的极值问题转换成无条件的极值问题进行研究。

一般把有条件的极值问题称为原问题，将其抽象为：

其有m个等式约束，p个不等式约束。

其拉格朗日函数为：

其中λ和μ都是每个约束函数的拉格朗日乘数。

通过拉格朗日函数可以把有约束的极值问题转换成无约束条件的对偶问题进行研究。

接下来把拉格朗日函数的λ和μ看作常量，在x定义域内对拉格朗日取极小值，就有拉格朗日对偶函数：

此时原问题化为拉克朗日对偶函数取极大值的问题：

其中有一个对拉个朗日乘子的约束λ>=0

求解原问题的最优解一般定义为p*,对偶问题的最优解定义为d*,那么在凸优化领域里，原问题的解p*一定大于等于对偶问题的解d*，所以原问题是一个凸问题，那么这个等式就是成立的,即一个强对偶问题:

拉格朗日对偶函数就是求解关于o，e'和w下确界的一个函数，其中前两项(第一条橙线)都是关于o和e'的线性函数，如果要使它们的下确界存在，其限定函数的系数就必须为0，因此有：

又因为范数的共轭函数的限制，则w的共轭函数根据凸优化理论，第二条橙线要么等于0要么为负无穷，所以要使其下确界存在，则这一项必须为0，那么z的二范数就小于等于1.

则最后该问题简化为：

对对偶函数求取极大值。

因为原问题的极小值为求取对偶问题的最大值，在该问题中，对偶问题的最优解即原问题的最优解，所以只要找到保证对偶函数的最大值(d*)大于dmin，那么原问题也一定是大于dmin的

当满足对偶函数取最大值时得λ得μ的取值时，得到d*=dmin。

如果要使得主车和障碍物之间的距离大于dmin，只需要满足存在一组λm和μm满足下述不等式成立：

所以在MPC设计上，如果要保证规划的轨迹使主车和障碍物的距离大于dmin，就要有以下的不等式成立，这里作为MPC约束的碰撞约束。

另外还需要添加起点和终点的约束:

即规划的轨迹的起点是给定的起点x，y，θ；规划轨迹的终点是给定的终点x,y,θ；且每个点之间要保证车辆的运动学约束(x(k+1)和x(k)的关系)

此外状态量还要满足规划的极限，比如速度要在设定的范围内,x,y要在地图的可行驶范围之内，状态量最后一项的航向角是没有约束要求的：

输入量也要满足车辆的极限：

车辆横摆角速度的约束也要保证车辆横摆角速度的范围，主要是满足舒适性的要求。

MPC的目标函数就是对预测时域每个状态x(k)损失函数的一个求和，损失函数第一项要求车辆跟踪参考路径的变化，即车辆路径和A*算法路径越接近越好，另外为了提高舒适性，加速度要越小越好，为了满足连续性,MPC的第一个输入分量要和当前的输入状态尽可能接近，同时输入量的变化率越小越好，即加加速度和方向盘的转速越小越好。

最后就得到了cost函数(如上图)，用二范数表示每一个项。

最后OBCA规划问题就转化为如下的非线性优化问题：

apollo中通过IPOPT非线性规划求解器进行求解，之前在速度规划讲到的IPOPT求解器，其如果有一个好的初始解，可以加快其向最优解收敛的速度，所以这里用混合A*算法计算的轨迹作为OBCA算法的初始解。

这里还有对偶变量的初始解，通过对对偶变量初始化，即通过之前求解的有碰撞约束的对偶函数的优化求解。根据对偶函数的设计，把对偶问题的函数用负的dm(k)来表示。这样就把极大值问题转化为极小值问题进行求解，这样方便代入IPOPT的优化求解器：

对每个时间k的每个障碍物的距离求取最小值的和，即求和取最小值，求出的目标函数取最小值时的μ和λ就是对偶变量初始化的值。

但经过分析，约束有一个二次函数，这里就只能用非线性规划求解器进行求解：

为了提高求解效率，apollo对这里进行了一个优化，把二次约束放入到目标函数中，成为一个软约束，这样对偶变量初始化就成为了一个二次规划的问题，，就可以用OSQP求解器进行求解(dual_variable_warm_start_problem.cc)

所以整个OBCA算法就是DISTANCE_APPROACH_IPOPT_FIXED_TS算法

此外，apollo中还有几个OBCA算法的衍生算法：

第一个是采样时间可变，原来的采样时间是ts，所以如何优化都是在最后时间到达终点的，这里增加一个采样时间系数t(k),采样时间就从固定时间ts变成了ts.t(k),就可以缩短到达终点的时间。

约束函数变为：

另外目标函数也增加了对时间系数的惩罚，包括了对二次和一次的损失函数，期望时间系数越小越好，因为越小到达的终点时间越早。

之前算法的终点都是硬约束，硬约束会导致IPOPT求解速度变慢，甚至极端情况下会找不到可行的解，但在一些场景下，我们并不需要车辆严格到达正好的x，y和theta的状态，到达终点附近也是能满足我们的需求的，因此Apollo做了进一步优化，这里将硬约束转化成了软约束，即在目标函数里增加了到达终点状态的一个惩罚项，同时对终点进行了一个松弛，这样就得到了Apollo中的DISANCE_APPROACH_IPOPT_RELAX_END这个函数。

接下来讲解DL-IAPS规划算法：

虽然OBCA算法通过凸优化的强对偶性很好的解决了在开放空间和障碍物的一个无碰撞的约束，但是算法求解效率和鲁棒性是比较差的，这里单次求解时长可能达到一秒左右，而且随着障碍物的数量以及障碍物边数的增加，还会导致求解效率降低甚至求不出解的可能，所以APOLLO设计了一种横纵向解耦的开放空间路径规划算法。

DL-IAPS路径规划算法是一种分段的路径规划算法，其和OBCA算法不同，OBCA算法是将整条路径一起进行平滑，是首先将混合A*产生的一个完整的轨迹根据轨迹的前进或者后退分成不同的段，并在每段分段进行平滑，同时保证平滑后的路径不会和障碍物发生碰撞，以及平滑后的路径满足最大的曲率约束，对于这种算法的速度规划采用PJSO算法，其和上节课讲到的基于二次规划的速度规划算法是比较类似的，在DL-IAPS规划的路径上分别对位置、速度以及加速度进行采样，并通过二次优化进行求解。

DL-IAPS即双循环迭代锚点路径平滑算法，上图为该算法的伪代码，其主要包含了两层循环，外层循环是处理和障碍物碰撞约束的循环Collision Check，内层循环是路径平滑的一个循环，对于开放空间路径规划算法其难点主要在于障碍物的碰撞约束难以求解，在OBCA算法构架上有障碍物无碰撞约束，但是导致其求解效率非常低。Apollo设计了一种迭代的方法去求解障碍物约束。

之前讲到了参考线散点的平滑算法，对于每个散点构造一个x，y的矩形框作为每个散点位置的一个约束

在DL-IAPS算法也同样通过这种方法进行路径的平滑，但是在每个迭代平滑完成后，结果会和所有的障碍物进行一个碰撞检查，如果发生了碰撞，那么发生碰撞的参考点调小其矩形框的大小重新进行下一次的平滑，不断迭代直到满足碰撞约束为止。

在参考线算法中是通过三个点对两个向量求和来表示平滑度，同时推导出其曲率约束关系式

这里曲率约束的关系式是非线性的，如果考虑曲率约束的话只能采用非线性优化进行求解，在参考线平滑算法中，参考线一般来自地图的车道线，但是它曲率本身就是比较小的，另外应用于参考线平滑点的数量比较多，对实时性的要求比较高，所以参考线平滑算法采用了不考虑曲率约束的二次规划问题进行求解，但是对于开放空间算法，参考路径是来自于混合A*搜索的结果，参考路径本身的曲率就是比较高的，就必须把曲率约束考虑进来。Apollo中采用了一种SQP的二次规划算法来解决非线性的约束问题。

首先对约束函数进行线性化(泰勒展开，保留一次项，但是需要求解点附近的一个参考点X0的函数值和导数值)：

可以采用上次平滑的结果作为本次的参考点，同时对优化点增加一个可信区间约束：

避免上次规划点和这次约束过远。

以上为Sub-problem的过程。

在SQP外层为Penalty iteration，是一个曲率惩罚的循环，是对曲率的软约束，如果存在违背曲率约束的求解的话，就会调高曲率约束的松弛变量，对权重进行平滑，所以优化问题简化为如下的二次规划问题。这里优化函数包含两项，第一项为相邻两点的平滑度的代价，第二项是曲率约束的松弛变量，这里前两个约束分别是起点和终点，要和给定的起点和终点坐标相同，第三个约束是起始点航向角，方向要和给定的方向要相同，第四个约束是终点的航向角和给定的航向角相等，第五个和第六个约束是坐标要在给定的矩形框之内，矩形框大小主要是在外层的Collison Check循环当中进行更新，第七个和第八个约束是使坐标要在可信区间范围内，主要是保证在Sub-problem中每次迭代优化结果都不会偏离太远，即保证曲率线性化约束的准确性，第九个约束是曲率约束的线性化求解函数，就是之前泰勒展开的函数，其输入包括上次规划的结果作为当前规划的参考节点，最后一个约束是松弛变量约束，保证松弛变量大于等于0.

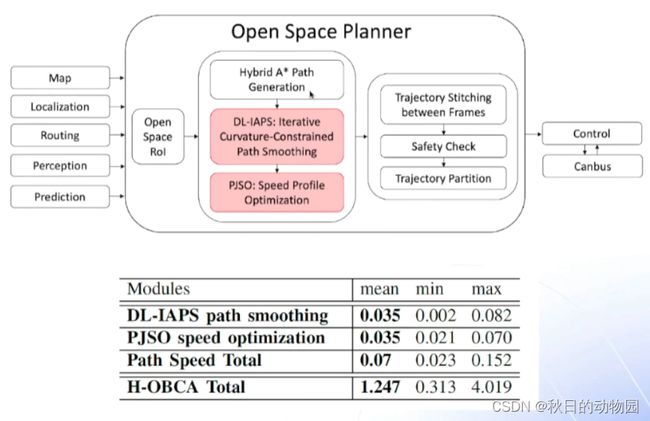
以下为DL-IAPS算法对OPEN SPACE PLANNER的整体架构：

首先是通过OPEN SPACE ROI decider确定一个可行驶的区域，然后通过混合A*算法搜索出一条粗糙的轨迹，然后通过DL-IAPS算法对粗糙轨迹的路径进行平滑得到一条满足曲率约束且无碰撞的路径，接下来对平滑后的路径进行一个速度规划，最后生成一条轨迹。上图中包含了对各算法计算时间的统计。