AcWing 1077. 皇宫看守（树形DP + 状态机DP）

一、问题

二、分析

1、思路分析

在讲解这道题之前，大家需要对状态机DP有一定的了解，如果不了解或者不太清楚的话，可以先去看作者之前的文章：第四十七章 动态规划——状态压缩模型

我们用下面的图进行分析：

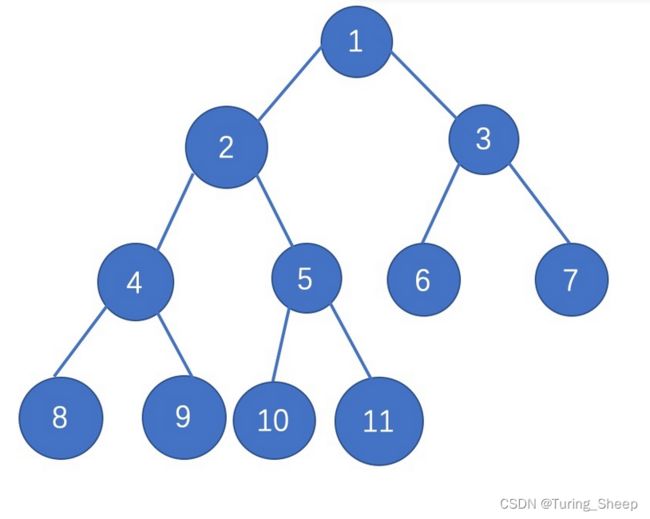
我们以2号点为例子，观察一下能够看到2号点的点：
2号点的父节点：1

2号点的子节点：4和5

2号点自己

如果我们不选2号点的话，分为下面两种情况：
第一种：
如果2号点能够被父节点看到的话，那么2号点的子节点4和5选不选都行。因为2号点已经有人能看到了。
第二种：
如果2好点能够被子节点看到的话，那么2号点的子节点至少选一个，由于题目中要求的是最小，所以我们只要在子节点中选一个就行。

如果我们选了2号点，即2号点能够被自己看到的话：

子节点随便选，挑一个最小值的就行。

我们发现2号点选和不选对于子树的选择也产生了一定的影响，因此我们需要采用状态机DP。

2、状态表示

$f[u][j]$表示在以$u$为根节点的树中，当$u$的状态是$j$的时候，我们选择的最少节点。

其中：

$j=0$的时候，表示$u$不选，但是$u$能够被父亲观察到。

$j=1$的时候，表示$u$不选，但是$u$能够被子节点看到。

$j=2$的时候，表示选$u$,$u$至少能被自己看到。

3、状态转移

我们一个情况一个情况的分析：

$j=0$的时候

$u$没选，那么对于其子节点而言，$f[son][0]$就是不存在的，因为这个状态是说没有选节点$son$，但是$son$能够被父节点观察到。我们根本就没选它的父节点$u$，又怎么会被观察到呢？所以这种情况不存在。

那么由于$u$已经被父节点观察到了，那么他的子节点$son$选或者不选，能被谁看到，对于$u$而言是不重要的，我们只需要选出一个最小值即可。

那么针对每个子树都选出一个最小值，最后加在一起就行了。

$$f[u][0]=\sum min(f[son][1],f[son][2])$$

$j=1$的时候
$u$没选，并且$u$能够被子节点观察到，由于$u$没选，根据刚刚的理由，我们子节点状态中合法的只有两个了：$f[son][1]$和$f[son][2]$

题目中要求至少，也就是我们需要拿出一个son是必须选状态$f[son][2]$的，其余的在两个状态之间选出一个最小值，最后加在一起。

但是我们具体拿出来哪个还是不确定的，所以我们需要枚举一下，然后在所有的情况中再选最小值。

$$f[u][1]=min(f[so{n}_k][2]+\sum _{i\ne k}min(f[so{n}_i][1],f[so{n}_i][2]))$$

$j=2$的时候
这个情况是最好处理的，这种情况说明我们选了$u$，那么子节点的三种情况都可选，挑一个最小的就行。
$$f[u][2]=min(f[son][0],f[son][1],f[son][2])$$

4、循环设计

我们这个是1维的，所以写一个for循环就行，但是由于我们的这些节点存储在了树上，所以我们需要用DFS代替。

5、初末状态

$f[u][2]=v[u]$，因为这个状态说明我们选了节点$u$。

三、代码

由于是从根节点开始，所以需要选出根节点，即我们标记所有的子节点，最后剩下的就是根节点$root$。

#include
using namespace std;
const int N = 1510, M = 2 * N;
const int INF = 0x3f3f3f3f;
int h[N], e[M], ne[M], v[N], idx;
bool son[N];
int n;
int f[N][3];
void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
	f[u][2] = v[u];
	int sum = 0;
	for(int i = h[u]; i != -1; i = ne[i])
	{
		int j = e[i];
		dfs(j);
		f[u][0] = f[u][0] + min(f[j][1],f[j][2]);
		f[u][2] = f[u][2] + min(min(f[j][0], f[j][1]), f[j][2]); 
		sum += min(f[j][1], f[j][2]);
	}
	f[u][1] = INF;
	for(int i = h[u]; i != -1; i = ne[i])
	{
		int j = e[i];
		f[u][1] = min(f[u][1], sum - min(f[j][1], f[j][2]) + f[j][2]);
	}
}
int main()
{
	memset(h, -1, sizeof h);
	cin >> n;
	int root = 1;
	for(int i = 0; i < n; i ++ )
	{
		int j, k, m;
		cin >> j >> k >> m;
		v[j] = k;
		while(m -- )
		{
			int a;
			cin >> a;
			add(j, a);
			son[a] = true;
		}
	}
	while(son[root])root ++;
	dfs(root);
	cout << min(f[root][1], f[root][2]) << endl;
}