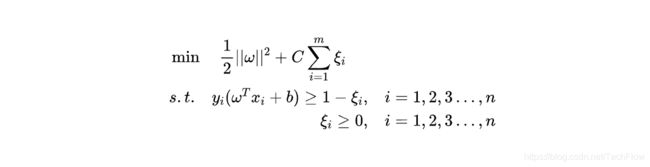机器学习，详解SVM软间隔与对偶问题

今天是机器学习专题的第34篇文章，我们继续来聊聊SVM模型。

我们在上一篇文章当中推导了SVM模型在硬间隔的原理以及公式，最后我们消去了所有的变量，只剩下了$\alpha$。在硬间隔模型当中，样本是线性可分的，也就是说-1和1的类别可以找到一个平面将它完美分开。但是在实际当中，这样的情况几乎是不存在的。道理也很简单，完美是不存在的，总有些样本会出错。

那针对这样的问题我们应该怎么解决呢？

软间隔

在上文当中我们说了，在实际的场景当中，数据不可能是百分百线性可分的，即使真的能硬生生地找到这样的一个分隔平面区分开样本，那么也很有可能陷入过拟合当中，也是不值得追求的。

因此，我们需要对分类器的标准稍稍放松，允许部分样本出错。但是这就带来了一个问题，在硬间隔的场景当中，间隔就等于距离分隔平面最近的支持向量到分隔平面的距离。那么，在允许出错的情况下，这个间隔又该怎么算呢？

为了解决这个问题，我们需要对原本的公式进行变形，引入一个新的变量叫做松弛变量。松弛变量我们用希腊字母$\xi$来表示，这个松弛变量允许我们适当放松$y_i({\omega }^T{x}_i+b)\ge 1$这个限制条件，我们将它变成$y_i({\omega }^T{x}_i+b)\ge 1-{\xi }_i$。

也就是说对于每一条样本我们都会有一个对应的松弛变量${\xi }_i$，它一共有几种情况。

1. $\xi =0$，表示样本能够正确分类
2. $0<\xi <1$，表示样本在分割平面和支持向量之间
3. $\xi =1$，表示样本在分割平面上
4. $\xi \ge 1$，表示样本异常

我们可以结合下面这张图来理解一下，会容易一些：

松弛变量虽然可以让我们表示那些被错误分类的样本，但是我们当然不希望它随意松弛，这样模型的效果就不能保证了。所以我们把它加入损失函数当中，希望在松弛得尽量少的前提下保证模型尽可能划分正确。这样我们可以重写模型的学习条件：

这里的C是一个常数，可以理解成惩罚参数。我们希望$||\omega |{|}^2$尽量小，也希望$\sum {\xi }_i$尽量小，这个参数C就是用来协调两者的。C越大代表我们对模型的分类要求越严格，越不希望出现错误分类的情况，C越小代表我们对松弛变量的要求越低。

从形式上来看模型的学习目标函数和之前的硬间隔差别并不大，只是多了一个变量而已。这也是我们希望的，在改动尽量小的前提下让模型支持分隔错误的情况。

模型推导

对于上面的式子我们同样使用拉格朗日公式进行化简，将它转化成没有约束的问题。

首先，我们确定几个值。第一个是我们要优化的目标：$f(x)={\min }_{\omega ,b,\xi }\frac{1}{2}||\omega |{|}^2+C{\sum }_{i=1}^m{\xi }_i$

第二个是不等式约束，拉格朗日乘子法当中限定不等式必须都是小于等于0的形式，所以我们要将原式中的式子做一个简单的转化：

$$\begin{array}{r}g(x)=1-{\xi }_i-y_i({\omega }^T{x}_i+b)\le 0\\ h(x)=-{\xi }_i\le 0\end{array}$$

最后是引入拉格朗日乘子: $\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m),\beta =({\beta }_1,{\beta }_2,\cdots ,{\beta }_m)$

我们写出广义拉格朗日函数：$L(\omega ,b,\xi ,\alpha ,\beta )=\frac{1}{2}||\omega |{|}^2+C{\sum }_{i=1}^m{\xi }_i,+{\sum }_{i=1}^m{\alpha }_i(1-{\xi }_i-y_i({\omega }^T{x}_i+b))-{\sum }_{i=1}^m{\beta }_i{\xi }_i$

我们要求的是这个函数的最值，也就是${\min }_{\omega ,b,\xi }{\max }_{\alpha \ge 0,\beta \ge 0}L(\omega ,b,\xi ,\alpha ,\beta )$。

在处理硬间隔的时候，我们讲过对偶问题，对于软间隔也是一样。我们求L函数的对偶函数的极值。

对偶问题

原函数的对偶问题是${\max }_{\alpha \ge 0,\beta \ge 0}{\min }_{\omega ,b,\xi }L(\omega ,b,\xi ,\alpha ,\beta )$，这个对偶问题要成立需要满足KKT条件。

我们先把这个KKT条件放一放，先来看一下对偶问题当中的内部的极小值。这个极小值没有任何约束条件，所以我们可以放心大胆地通过求导来来计算极值。这个同样是高中数学的内容，我们分别计算$\frac{\partial L}{\partial \omega }$，$\frac{\partial L}{\partial b}$和$\frac{\partial L}{\partial \xi }$。

求导之后，我们可以得到：

$$\begin{array}{rl}\frac{\partial L}{\partial \omega }=0& \to \omega =\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\\ \frac{\partial L}{\partial b}=0& \to \sum _{i=1}^m{\alpha }_i{y}_i=0\\ \frac{\partial L}{\partial \xi }=0& \to {\beta }_i=C-{\alpha }_i\end{array}$$

我们把这三个式子带入对偶函数可以得到：

$$\begin{array}{rl}L(\omega ,b,\xi ,\alpha ,\beta )& =\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{\alpha }_i(1-{\xi }_i)-\sum _{i=1}^m(C-{\alpha }_i){\xi }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$

由于${\beta }_i\ge 0$，所以我们可以得到$0\le {\alpha }_i\le C$，所以最后我们可以把式子化简成：

将原始化简了之后，我们再回过头来看KKT条件。KKT条件单独理解看起来有点乱，其实我们可以分成三个部分，分别是原始问题可行：

$$\begin{array}{r}1-{\xi }_i-y_i({\omega }^T{x}_i+b)\le 0\\ -{\xi }_i\le 0\end{array}$$

对偶问题可行：

$$\begin{array}{r}{\alpha }_i\ge 0\\ {\beta }_i=C-{\alpha }_i\end{array}$$

以及松弛可行：
$$\begin{array}{r}{\alpha }_i(1-\xi -y_i({\omega }^T{x}_i+b))=0\\ {\beta }_i{\xi }_i=0\end{array}$$

我们观察一下倒数第二个条件：${\alpha }_i(1-\xi -y_i({\omega }^T{x}_i+b))=0$。

这是两个式子相乘并且等于0，无非两种情况，要么${\alpha }_i=0$，要么后面那串等于0。我们分情况讨论。

1. 如果${\alpha }_i=0$，那么$y_i({\omega }^T{x}_i+b)-1\ge 0$，样本分类正确，不会对模型产生影响。
2. 如果${\alpha }_i>0$，那么$y_i({\omega }^T{x}_i+b)=1-{\xi }_i$，则样本是支持向量。由于$C={\alpha }_i+{\beta }_i$ ，并且${\beta }_i{\xi }_i=0$。我们又可以分情况：
   1. ${\alpha }_i<C$，那么${\beta }_i>0$，所以${\xi }_i=0$，那么样本在边界上
   2. 如果${\alpha }_i=C$，那么${\beta }_i=0$，如果此时$\xi \le 1$，那么样本被正确分类，否则样本被错误分类

经过了化简之后，式子当中只剩下了变量$\alpha$，我们要做的就是找到满足约束条件并且使得式子取极值时的$\alpha$，这个$\alpha$要怎么求呢？我们这里先放一放，将在下一篇文章当中详解讲解。

今天的文章到这里就结束了，如果喜欢本文的话，请来一波素质三连，给我一点支持吧（关注、转发、点赞）。

原文链接，求个关注