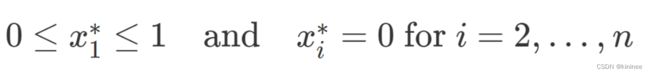jMetal学习笔记(二)-NSGAii源码解读

前言

上篇笔记根据使用手册介绍了jMetal的架构，但是由于使用手册撰写时间太早(最近更新时间是08年)，现在jmetal框架更新了，所以很多都已经不适用，这篇笔记会穿插讲解jmetal架构知识。
其实github也有jmetal文档，但是这份文档也比较旧了，应该是jmetal15年升级到maven的时候写的，但是参考性比手册要高

参考资料

jmetal4.5.userManual.pdf
jMetal/jMetalDocumentation
Alberto-00/EasyPass-AI
jMetal 使用教程（一）
jMetal 使用教程（二）
A fast and elitist multiobjective genetic algorithm
遗传算法之NSGA-Ⅱ原理分析和代码解读

使用NSGAii解决ZDT1

这部分可以先按照参考资料jMetal 使用教程（一，二），跑通这个案例，再来读代码。

主函数解读

首先，这个教程用的是5.2这个版本，注意不同版本的源码不一样，不要搞混了。
根据ZDT1_jMetal.java这个文件就可以看出，使用jmetal是可以有很多代码可以重复使用的比如

/**
 * Solve ZDT1 with NSGA-II on jMetal
 */
public class ZDT1_jMetal {
    public static void main(String[] args) throws FileNotFoundException {
        //问题集
        Problem<DoubleSolution> problem;
        //算法集
        Algorithm<List<DoubleSolution>> algorithm;
        //交换算子
        CrossoverOperator<DoubleSolution> crossover;
        //变异算子
        MutationOperator<DoubleSolution> mutation;
        //选择算子
        SelectionOperator<List<DoubleSolution>, DoubleSolution> selection;
        //帕累托前沿
        String referenceParetoFront = "";
        
        //定义优化问题，这个地方ZDT1()这个问题需要我们自己定义
        problem = new ZDT1(); 
        //配置SBX交叉算子
        double crossoverProbability = 0.9;
        double crossoverDistributionIndex = 20.0;
        crossover = new SBXCrossover(crossoverProbability, crossoverDistributionIndex);
        //配置变异算子
        double mutationProbability = 1.0 / problem.getNumberOfVariables();
        //  double mutationDistributionIndex = 20.0 ;
        mutation = new SimpleRandomMutation(mutationProbability);
        //配置选择算子
        selection = new BinaryTournamentSelection<DoubleSolution>(
                new RankingAndCrowdingDistanceComparator<DoubleSolution>());
        //将组件注册到algorithm
        algorithm = new NSGAIIBuilder<DoubleSolution>(problem, crossover, mutation)
                .setSelectionOperator(selection)
                .setMaxEvaluations(25000)
                .setPopulationSize(100)
                .build();
/*       或者用这样的方法注册一个算法
          evaluator = new SequentialSolutionListEvaluator();
          algorithm = new NSGAII(problem, 25000, 100, crossover,
          mutation, selection, evaluator);
*/
        //用AlgorithmRunner运行算法
        AlgorithmRunner algorithmRunner = new AlgorithmRunner.Executor(algorithm).execute();
        //获取结果集
        List<DoubleSolution> population = algorithm.getResult();
        long computingTime = algorithmRunner.getComputingTime();
        JMetalLogger.logger.info("Total execution time: " + computingTime + "ms");
        //将全部种群打印到文件中
        printFinalSolutionSet(population);
        if (!referenceParetoFront.equals("")) printQualityIndicators(population, referenceParetoFront);
    }
}

而以上代码中需要我们自己操作的是：

• 根据实际情况新建一个myproblem类，然后在main中就可以用myproblem类新建对象

        //定义优化问题，这个地方ZDT1()这个问题需要我们自己定义
        problem = new ZDT1(); 

• 根据需要选择不同的算子，比如选择算子用二进制锦标赛算子，交叉算子用SBXCrossover

        //配置选择算子
        selection = new BinaryTournamentSelection<DoubleSolution>(
                new RankingAndCrowdingDistanceComparator<DoubleSolution>());
          //配置SBX交叉算子
        double crossoverProbability = 0.9;
        double crossoverDistributionIndex = 20.0;
        crossover = new SBXCrossover(crossoverProbability, crossoverDistributionIndex);              
                

• 在注册算法的时候，将参数传入，比如种群大小，评估次数

        //将组件注册到algorithm
        algorithm = new NSGAIIBuilder<DoubleSolution>(problem, crossover, mutation)
                .setSelectionOperator(selection)
                .setMaxEvaluations(25000)
                .setPopulationSize(100)
                .build();

创建myproblem类

根据以上需要我们做的，可以看到第二，三问题都不大，主要是如何创建myproblem类
ZDT1有30个决策变量，其定义如下：

最优情况下，决策变量的值为：

要定义myproblem就必须实现jMetal的problem

package org.uma.jmetal.problem;
public interface Problem<S extends Solution<?>> extends Serializable {
  /* Getters */
  每个问题都以决策变量的数量、目标函数的数量和约束的数量为特征，因此必须定义返回这些值的getter方法
  public int getNumberOfVariables() ;
  public int getNumberOfObjectives() ;
  public int getNumberOfConstraints() ;
  public String getName() ;

  /* Methods */
  有了问题才能有solution的类型，所以
  提供一个createsolution（）'方法来创建新的解决方案
  public S createSolution() ;
  还需一个评估方法，去评估problem的所有solution集
  public void evaluate(S solution) ;

Solution 接口是通用的，因此 jMetal 5 有许多接口对其进行扩展以表示double（即连续）问题、二进制问题等。
实现 Double Problem 的问题只接受 Double Solution 对象，并且必须实现获取每个变量的下限和上限的方法。
jMetal 5 提供了一个默认的抽象类，它实现了称为 [Abstract Double Problem]
对于 ZDT1这个问题，我们需要继承AbstractDoubleProblem，在具体类中定义需要解决的问题，在构造函数中获取变量上下限，overide evaluate () 来定义优化函数，有需要还要重写createSolution()；
构造函数部分：

public class ZDT1 extends AbstractDoubleProblem {

    /** Constructor. Creates default instance of problem ZDT1 (30 decision variables) */
     无参构造：这里的this就是调用兄弟构造器，将默认值30传入
    public ZDT1() {
        this(30);
    }

     有参构造
    public ZDT1(Integer numberOfVariables) {
        //继承父类的变量
        setNumberOfVariables(numberOfVariables);//设定决策变量个数，30
        setNumberOfObjectives(2);//设定优化目标函数个数,2
        setName("ZDT1");//给这个问题起名,ZDT1.

        //容量为30的列表
        List<Double> lowerLimit = new ArrayList<>(getNumberOfVariables()) ;
        List<Double> upperLimit = new ArrayList<>(getNumberOfVariables()) ;

        //设置定义域
        for (int i = 0; i < getNumberOfVariables(); i++) {
            lowerLimit.add(0.0); //每一个元素都设置为0
            upperLimit.add(1.0); //每一个元素都设置为1
        }
        设置变量的上下限
        //父类函数 
        setLowerLimit(lowerLimit);
        setUpperLimit(upperLimit);
    }

评估函数部分：评估函数的目的是设置solution的目标函数值

    //虽然写的是DoubleSolution,但是后期会传入实现类 多态
    public void evaluate(DoubleSolution solution) {
        double[] f = new double[getNumberOfObjectives()]; //目标数量？

        f[0] = solution.getVariableValue(0);
        double g = this.evalG(solution);
        double h = this.evalH(f[0], g);
        f[1] = h * g;
        //设置目标函数值-最终目的
        solution.setObjective(0, f[0]);
        solution.setObjective(1, f[1]);
    }

    private double evalG(DoubleSolution solution) {实现g函数 }

    public double evalH(double f, double g) {实现h函数 }

evaluate & createsolution

但是设置完，有些问题，这个evaluate在哪会用到呢，在主函数也没看到它的使用啊？还要不是说有createsolution函数吗？在哪呢？

别急，遇到问题，我们逐一突破 (๑•̀ㅂ•́)و✧
首先是evaluate在哪用到？
来看看mian方法，和算法有关的就是这句代码

        //将组件注册到algorithm
        algorithm = new NSGAIIBuilder<DoubleSolution>(problem, crossover, mutation)
                .setSelectionOperator(selection)
                .setMaxEvaluations(25000)
                .setPopulationSize(100)
                .build();
        //用AlgorithmRunner运行算法
        AlgorithmRunner algorithmRunner = new AlgorithmRunner.Executor(algorithm).execute();

欸，又奇怪了，在文档中明明用的是nsgaii.java，为什么这里没有用到呢？我做了一张图，总的来说的最后还是创建的nsgaii对象，并且真正的执行过程其实在其run方法中。

那么要找的答案就在run方法中的offspringPopulation = this.evaluatePopulation(offspringPopulation);如下图所示，promblem的evaluate就找到啦
(里面有个instanceof 是 Java 的保留关键字，它的作用是测试它左边的对象是否是它右边的类的实例，返回 boolean 的数据类型)

第二个问题：createsolution函数在哪？
打开ZDT1的父类 AbstractDoubleProblem，可以看到该函数，返回了一个DefaultDoubleSolution对象

 public DoubleSolution createSolution() {
        return new DefaultDoubleSolution(this);

而DefaultDoubleSolution对象就是继承 AbstractGenericSolution

public class DefaultDoubleSolution extends AbstractGenericSolution<Double, DoubleProblem> implements DoubleSolution {
    public DefaultDoubleSolution(DoubleProblem problem) {
        super(problem);
        this.initializeDoubleVariables();
        this.initializeObjectiveValues();
    }

所有当我们需要自定义solution是，可以继承DefaultDoubleSolution，在具体类里面定义编码方案，定义决策变量，定义优化目标函数储存方法

run方法解析

遗传算法的核心步骤就在run方法

        public void run() {
            方法中新建population的list，里面添加soulution,这时候就用到了problem的创建solution方法
            this.population = this.createInitialPopulation();
            将交给评估器评估，返回population
            this.population = this.evaluatePopulation(this.population);
            初始化迭代计数器（初始值为 1，因为假设初始种群已经被评估）
            this.initProgress();
            没有达到终止条件
            while(!this.isStoppingConditionReached()) {
                Selection()方法必须从种群中创建一个交配池，它执行了选择算子
                List<S> matingPopulation = this.selection(this.population);
                reproduction() 方法将交叉和变异算子应用于交配种群，从而将新个体添加到后代种群中
                List<S> offspringPopulation = this.reproduction(matingPopulation);
                评估
                offspringPopulation = this.evaluatePopulation(offspringPopulation);
                重点：replacement() 方法通过应用排序和拥挤距离选择将当前种群和后代种群连接起来以产生下一代种群：
                this.population = this.replacement(this.population, offspringPopulation);
                增加计数器
                this.updateProgress();
            }

(1) this.population = this.createInitialPopulation();
下面就是方法具体内容，用到了problem的createSolution方法，并把产生的solution个体加入到种群list中

    protected List<S> createInitialPopulation() {
        List<S> population = new ArrayList(this.getMaxPopulationSize());

        for(int i = 0; i < this.getMaxPopulationSize(); ++i) {
            S newIndividual = this.getProblem().createSolution();
            population.add(newIndividual);
        }

        return population;
    }

problem的createSolution方法的时候，会返回一个 DefaultDoubleSolution，
而DefaultDoubleSolution会自动初始化决策变量和目标函数值，将随机值注入其中
this.initializeDoubleVariables();
this.initializeObjectiveValues();
下面是initializeDoubleVariables()方法

private void initializeDoubleVariables() {
    疑问？什么是决策变量，为什么一个solution要设置那么多决策变量
    答：决策变量就是x，其个数就是x的维度
    ZDT1问题的f2中的求和表达式30个x相加，所以维度为30.。
    假设目标函数是y ＝f(x)，决策变量就是这个x，V就是x的维度。比如求二元函数y＝x1^3-x2^2的极值，V就是2，对应[x1, x2].
        for(int i = 0; i < ((DoubleProblem)this.problem).getNumberOfVariables(); ++i) {
            Double value = this.randomGenerator.nextDouble(this.getLowerBound(i), this.getUpperBound(i));
            this.setVariableValue(i, value);
        }

    }

(2) this.population = this.evaluatePopulation(this.population);
对产生的种群，需要重新计算决策变量对应的目标函数值(上面将evaluate方法的时候有详细说明)

(3) List <泛型S> matingPopulation = this.selection(this.population);
这步是为了创建交配池，用到的selection()方法，主要是调用传入进来的选择算子
在主函数里，传入的是二进制锦标赛算子，它的工作原理：
就是我们再整个种群中抽取n个个体，让他们进行竞争(锦标赛)，抽取其中的最优的个体。参加锦标赛的个体个数成为tournament size。通常当n=2便是最常使用的大小，也称作Binary Tournament Selection.
Tournament Selection的优势:
更小的复杂度 O(n)
易并行化处理
不易陷入局部最优点
不需要对所有的适应度值进行排序处理

    protected List<S> selection(List<S> population) {
        List<S> matingPopulation = new ArrayList(population.size());
疑问：为什么要先选择一下，再加入交配池，个体数量应该是不变的？
        for(int i = 0; i < this.getMaxPopulationSize(); ++i) {
            S solution = (Solution)this.selectionOperator.execute(population);
            matingPopulation.add(solution);
        }

        return matingPopulation;
    }

(4) List<泛型S> offspringPopulation = this.reproduction(matingPopulation);
reproduction() 方法将交叉和变异算子应用于交配种群，从而将新个体添加到后代种群中

    protected List<S> reproduction(List<S> population) {
        int numberOfParents = this.crossoverOperator.getNumberOfParents();
        this.checkNumberOfParents(population, numberOfParents);
        List<S> offspringPopulation = new ArrayList(this.getMaxPopulationSize());

        for(int i = 0; i < this.getMaxPopulationSize(); i += numberOfParents) {
            List<S> parents = new ArrayList(numberOfParents);

            for(int j = 0; j < numberOfParents; ++j) {
                parents.add(population.get(i + j));
            }

            List<S> offspring = (List)this.crossoverOperator.execute(parents);
            Iterator var7 = offspring.iterator();

            while(var7.hasNext()) {
                S s = (Solution)var7.next();
                this.mutationOperator.execute(s);
                offspringPopulation.add(s);
            }
        }

        return offspringPopulation;
    }

(5) this.population = this.replacement(this.population, offspringPopulation);
重点：replacement() 方法通过应用排序和拥挤距离选择将当前种群和后代种群连接起来以产生下一代种群

    protected List<S> replacement(List<S> population, List<S> offspringPopulation) {
        List<S> jointPopulation = new ArrayList();
        jointPopulation.addAll(population);
        jointPopulation.addAll(offspringPopulation);
        快速非支配排序
        Ranking<S> ranking = this.computeRanking(jointPopulation);
        拥挤距离选择
        return this.crowdingDistanceSelection(ranking);
    }
    上面调用了computeRanking方法，而重点就是调用DominanceRanking().computeRanking
    protected Ranking<S> computeRanking(List<S> solutionList) {
        Ranking<S> ranking = new DominanceRanking();
        ranking.computeRanking(solutionList);
        return ranking;
    }    

DominanceRanking().computeRanking方法就是实现了非快速支配排序，本文就不放代码了，太长了，可能会出个视频讲解
视频已经出了，感兴趣的可以去看一下，讲的挺一般吧( =•ω•= )m
视频链接：nsgaii 快速非支配排序java代码讲解