排序知识盘点

---

排序

本章中将学习不同时空复杂度和应用情况下的排序算法思想，其功能都是一样的，就是完成一定顺序的排序，我们要根据不同的题目特点来选择适合的算法

知识框架

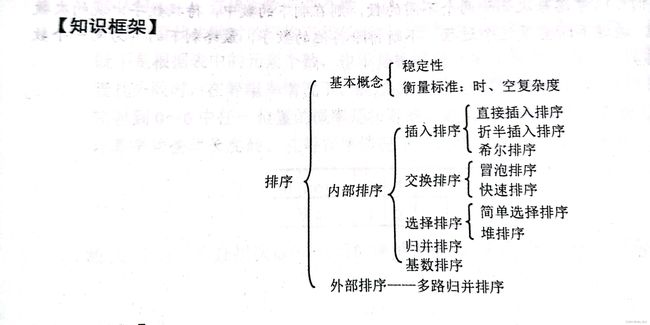
总的来说排序可以分为内部排序和外部排序两类，内部排序包括插入排序，交换，选择，归并等。外部排序包括多路归并排序。

---

排序的基本概念

排序的定义

排序就是重新排列表中的元素，使得表中的元素按关键字有序的过程排列。
排序要求算法的稳定性，即对同一个序列，相同值在排序完成后的相对次序也是和原来相同的，最为算法的一般要求，稳定性总是越稳定越好
根据数据元素是否在内存中，我们可以把排序算法分为内部排序和外部排序两类，
内部排序是指在排序期间元素全部存放在内存中的排序
外部排序是指在排序期间元素无法全部存放在内存中，必须在排序的过程中根据要求不断地在内外存之间移动的排序

---

插入排序

插入排序是一种比较简单的排序，其根本原理就是依次读取数据排出序列，每次将元素排序在符合的位置，我们通常把这个序列放在数组中，也就意味着对元素的排序实际上是对数组的操作

直接插入排序

在上面的这个序列中，我们用A[0]当作哨兵存储值，若当前值A[i]>A[i-1]（A[i-1]为序列最大值）则不用排序，直接入序列。若小于则需要找到其在序列中的位置，我们将这个要比对的值记为A[0]，然后依次比较前面的数值，若比其大则把那些数后移一位，若>=A[i],则当前的A[j]就是比A[i]小的数，A[j+1]=A[i]，而且由于哨兵的存在，如果遍历所有元素仍未找到>=A[i]的值，说明A[i]就是最小值，A[i]和A[0]比较必然是相等，则把A[i]排在A[0+1]=A[1]，即为第一位最小值

void InsertSort(Elemtype A[],int n){//从小到大排序
	//A[0]为哨兵，记录当前排序元素
	//0是哨兵，1只有一个元素不需要排序，因此从i=2开始排序
	int i,j;
	for(i=2;i<=n;i++){
		if(A[i]<A[i-1]){//如果新元素大于末尾元素（最大值）就不用排
			A[0]=A[i];//反正说明要排序，将其值放在哨兵
			for(j=i-1;A[0]<A[j];j--){//对比前面的i-1个元素，一旦找到比A[0]大的则为其所对应位置
				A[j+1]=A[j];}//元素后移
			A[j+1]=A[0];//A[j]大于等于其的值，排在A[j+1],如果到达A[0]则排在A[1]
		}//if
	}//for
}

---

折半插入排序

折半插入排序其实就是在直接排序中运用了折半查找，因为我们一个一个查找肯定效率不那么高，如果折半查找的话效率会高一点

void InsertSort(Elemtype A[],int n){//从小到大排序
	//A[0]为哨兵，记录当前排序元素
	//0是哨兵，1只有一个元素不需要排序，因此从i=2开始排序
	int mid=0,high=0,low=1,i,j;
	for(i=2;i<=n;i++){
		if(A[i]<A[i-1]){//如果新元素大于末尾元素（最大值）就不用排
			A[0]=A[i];//反正说明要排序，将其值放在哨兵
			low=1;high=i-1;mid=(low+high)/2;
			while(low<=high){
				if(A[i]=A[mid]){
					break;}
				else if(A[i]<A[mid]){
					high=mid-1;}
				else{
					low=mid+1;}
			}//while,mid即为第一个小于A[i]的数的位置
			mid=(low+high)/2;
			for(j=i-1;j>mid;j--){//对比前面的i-1个元素，一旦找到比A[0]大的则为其所对应位置
				A[j+1]=A[j];}//元素后移
			A[j+1]=A[0];//A[j]大于等于其的值，排在A[j+1],如果到达A[0]则排在A[1]
		}//if
	}//for
}

---

希尔排序

希尔排序是在减少了直接插入排序的排序表的规模上实现的
在直接插入排序中，我们每次排序遍历的是整个序列，而希尔排序通过设置步长将整个序列分成了多个子表，再对各个子表进行插入排序

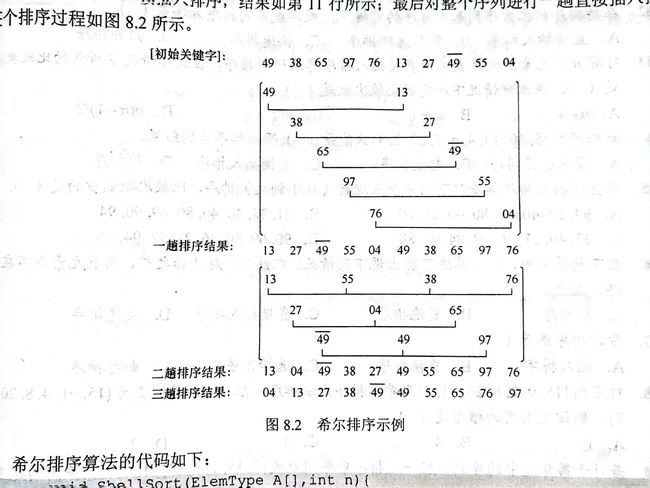
在上列希尔排序中我们可以看到，第一趟步长dk=全长/2=5，第一趟是两个元素比对排序
第二趟的步长是第一趟的一半=3，因此元素变多了，
第三趟的时候步长=1，当步长=1就是最后一趟了，大部分已经完成排序，只需对小部分调整即可

void ShellSort(ElemType A[],int n){
//A[0]不是哨兵，而是作为排序中的暂存单元,因此j不能越界
	int dk,i,j;
	for(dk=n/2;dk>=1;dk=dk/2){
		for(i=dk+1;i<=n;i++){
			if(A[i]<A[i-dk]){
				A[0]=A[i];//可以把A[0]当作一趟直接排序中的小哨兵，但是不能阻止越界
				for(j=i-dk;j>0 && A[0]<A[j];j=j-dk){
					A[j+dk]=A[j];}//其实不难发现，这段就是直接排序，只是间隔变成dk
				A[j+dk]=A[0];
			}//if
		}//for
	}//for
}

哈希排序不是一种稳定的排序法，对于相同的值，如果分到不同的子表里，会导致这些相同值的排序上的相对次序和原来序列产生不同，
一般哈希算法用于线性表的顺序存储

---

交换排序

插入排序是将需要排序的数值插入到某数前或后的位置，使用插入排序往往会导致整个数组的变动。而交换排序的本质则是每次交换两个数值的位置，不会造成整个数组的变动，因此交换排序是要更简单的。

冒泡排序

冒泡排序的意思是我们从后往前（也可从前往后），依次比对相邻两个数值的大小，如果不满足我们的大小排列次序则交换两个数值的值，依次遍历。这个过程中数值从后部往前部交换传递，就像气泡从底部浮到顶部一样，因此叫做冒泡排序。

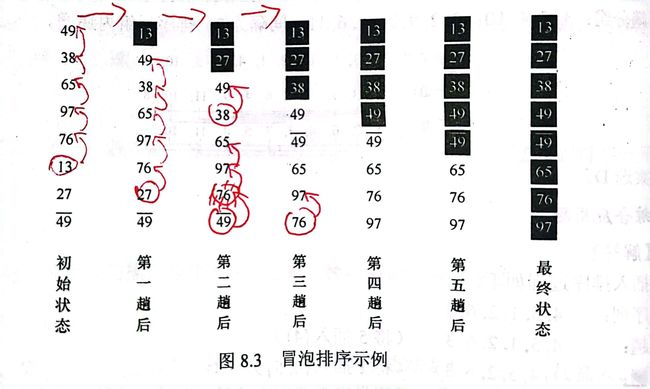
通常从前往后是升序排序，因此小的数值像泡泡上浮，大的数值像石头下沉

void BubbleSort(ElemType A[],int n){
	int mid;//交换中介
	bool flag=False;//判断是否进行交换
	for(int i=0;i<n;i++){//n个数排序n-1个即可
		flag=False;
		for(int j=n-1;j>i;j--){//i代表已经冒泡的数，除了j自身和冒泡的数，
							  //需要比较n-1-i个数，因此j>i	
			if(A[j-1]>A[j]){//往前比对
				mid=A[j];
				A[j]=A[j-1];
				A[j-1]=mid;
				flag=true;
			}//if
			if(flag==False){//不发生交换说明排序全部完成了
				return;}//直接退出即可	
		}//for j
	}//for i
}

---

快速排序

快速排序的过程是一个依次交替搜索和交换的过程


我们可以看到在上述序列的快速查找的过程中，以第一个元素49为比较基准（第一个49和最后一个49不是同一个数），图中空元素是基准49
以49为基准，先j从后往前，一旦搜索到比49小的数，则将其与 i 的位置替换
第二趟 i 则从前往后，找到大于基准49的数65，再将其与 j 的位置元素替换
第三趟再将 j 从后往前，找到小于49的数13，再与 i 的位置替换
以此类推，如此循环下来，最后直到 i==j 时，使得 i 之前的元素都小于49， i 之后的元素都大于49 ，我们将整个序列分为 1~ i-1 为小于等于49的序列，i==j 为基准49，j+1 ~ n为大于等于49的序列，在整个序列中有另一个49，由于这个49我们不会交换，所以它的位置取决于自己的序号是>i 还是 那么我们再对分出的两个序列使用快速排序，如果又有新序列可以再次快排，直到每个序列长度=1时结束
最后得到的就是我们所需的结果

void QuickSort(ElemType A[],int low,int high){
	if(low<high){
		//Partition()是划分操作，在其内进行上述的交换过程直到 low = high
		int pivotnum=Partiton(A,low,high);
		QucikSort(A,low,pivotnum-1);
		QuickSort(A,pivotnum+1,high);
	}//if
}

int Partition(ElemType A[],int low,int high){
	int pivot=A[low];
	while(low<high){
		while(low<high && A[high]>=privot){//while语句也可以用for循环内加if判断实现
			high--;//从后往前找到第一个小于基准的
		}//while
		A[low]=A[high];//可以直接赋值而不交换，因为基准已经保存在pivot里了
		while(low<high && A[low]<=privot){
			low++;
		}//while
		A[high]=A[low];
	}//while 当退出时low=high
	A[low]=privot;//最后把基准值放在中间
	return low;//返回基准值序号
}

快速排序最大的特点就是快速，快速排序是所有内排序算法中平均性能最优的排序算法。
但是快速排序并不具有稳定性。
注意：快速排序生成的子序列是无序的，依然需要子序列递归快速排序，且每趟排序后要把基准值放在最后退出循环的位置上。

---

选择排序

选择排序的思想和前两种不同，前两种是根据遍历的元素给他们安排合适的位置，选择排序则是直接按照顺序选择下一个元素。一般就是直接选择剩余序列中的最大/最小元素完成排序。

简单选择排序

简单选择就是直接从剩余序列中选择最大/最小元素按次序形成一个新序列

void SelectSort(ElemType A[] int n){
	int min=0;
	int B[n];
	for(int i=0;i<n;i++){
		min=0;
		for(int j=i+1;j<n;j++){
			if(A[i]<A[min]){
				min=i;
			}
		}//for
		if(min!=i){
			Swap(A[i],A[min]);}
	}//for
}

堆排序

我们把 n 个关键字序列L[1…n]称为堆，当且仅当序列满足

1. L(i) >= L(2i) 且 L(i) >= L(2i+1) 或
2. L(i) <= L(2i) 且 L(i) <= L(2i+1)

我们把情况1的堆称为大根堆，把情况2的堆称为小根堆
如果将这个一位数组的序列视作一颗完全二叉树，我们来看看

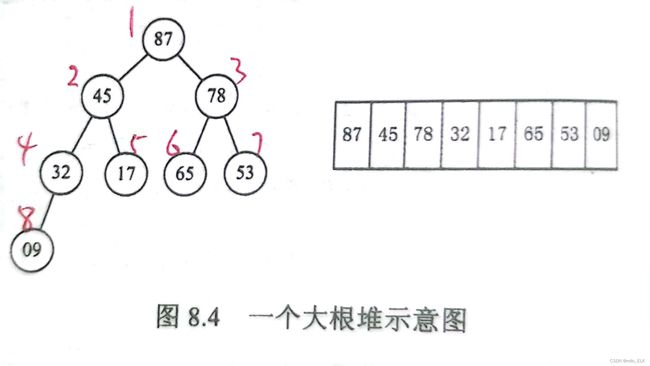
那么这种关系其实直观地来看，就是根节点与孩子结点的关系，
在这个完全二叉树中，根结点大于其两个孩子结点，我们就称之为大根堆
且其实兄弟结点之间并无大小关系限制，所以只需满足每个结点小于其父结点即可

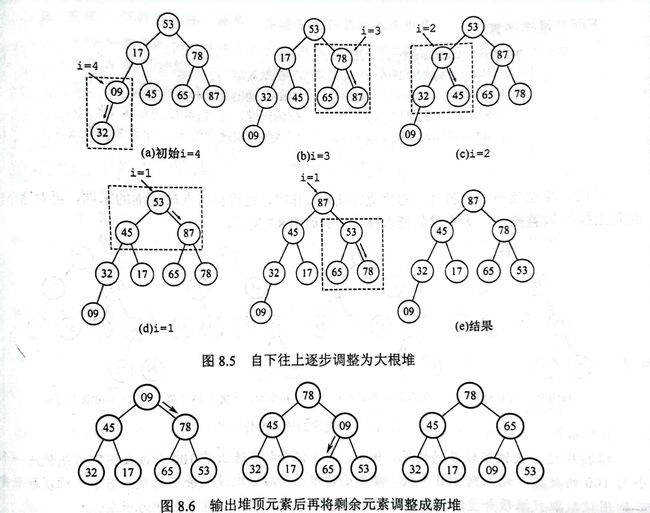
由于大根堆只需满足

1. L(i) >= L(2i) 且 L(i) >= L(2i+1)

所以若整个序列有n个元素，我们只需遍历n/2个元素，后n/2个元素会在我们遍历前面一半元素的时候进行调整
并且在完全二叉树里左孩子结点的序号是该结点的两倍
不难发现n/2一定是最后一个非叶子结点的序号

//形成大根堆
void BuildMaxHeap(ElemType A[],int n){
	for(int i=n/2;i>0;i--){
		HeadAdjust(A,i,n);}
}

//整理堆排序
void HeadAdjust(ElemType A[],int k,int n){
	//遍历 k 的两个孩子，只需选择其中最大值与 k 交换即可
	A[0]=A[k];//A[0]暂存根节点值
	for(int i=2*k;i<=n;i=2*i){//遍历子树以及它们的孩子，确保其中最大值在根部
		if(i<n && A[i]<A[i+1]){//i
			i++;//i指向更大的值
		}
		if(A[0]>A[i]) break;//如果根节点更大则筛选结束
		else{
			A[k]=A[i];
			k=i;
		}//else
	}//for
	A[k]=A[0];
}

//实现把大根堆从小到大排序
void HeadSort(ElemType A[],int n){
	BuildMaxHeap(A,len);
	for(int i=n;i>1;i--){
		Swap(A[i],A[1]); //把最大的换到最底部
		HeadAdjust(A,1,i-1); //重新调整剩余堆
	}
}

---

归并排序和基数排序

归并排序

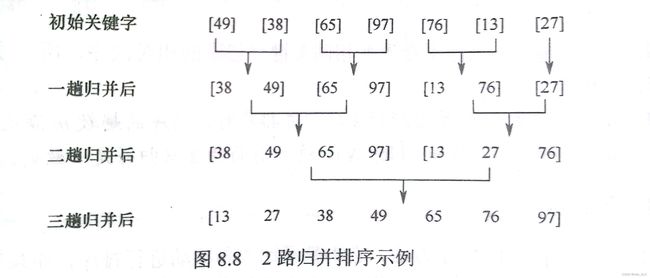
归并就是将两个或以上的序列合并为一个序列，每次我们是两两合并的
最开始的序列长度是1，一个元素自然不必排序，接下来两两合并，大于1的序列都需要进行排序
那么两个有序序列的合并，我们只需将其中一个序列的元素插入排序到另一个序列中即可
当最后只剩下一个序列，那么归并排序就完成了

ElemType *B=(ElemType *)malloc(sizeof(ElemType)*(n+1));//临时存储数组B至少可以容纳n+1个元素
//Merge()的功能是将前后两个有序表合并为一个有序表
void Merge(ElemType &A[],int low,int mid,int high){
//将A[low,mid],A[mid+1,high]两段合并
	int i,j,k;
	for(int q=low;q<=high;q++){
		B[q]=A[q];//B将两段顺序合并
	}
	for(i=low,j=mid+1,k=i;i<=mid && j<=high;k++){//i,j分别代表两个数组起始端,k代表当前A数组排序位置
		if(B[i]<=B[j]){//比较前面数组最小数和后面数组最小数
			A[k]=B[i];//重新赋值A，将元素较小的排在前面
			i++;
		}
		else{
			A[k]=B[j];//较小的排前面
			j++;
		}//else
	}//for
	while(i<=mid) A[k++]=B[i++];//剩余元素依次赋值给A
	while(j<=high) A[k++]=B[j++];//两个while只会进行一个
}

//合并子表获得排序结果
void MergeSort(ElemType A[],int low,int high){
	if(low<high){
		int mid=(low+high)/2;//从中间分为两半
		MergeSort(A,low,mid);//递归再分左半
		MergeSort(A,mid+1,high);//再分右半
		Merge(A,low,mid,high);//两半归并
	}//if
}

---

基数排序

基数排序是一种特别的排序方式，它不依赖于移动和比较，而是根据关键字各位的大小进行排序
其排序法有两种，一种是高位优先，一种是低位优先

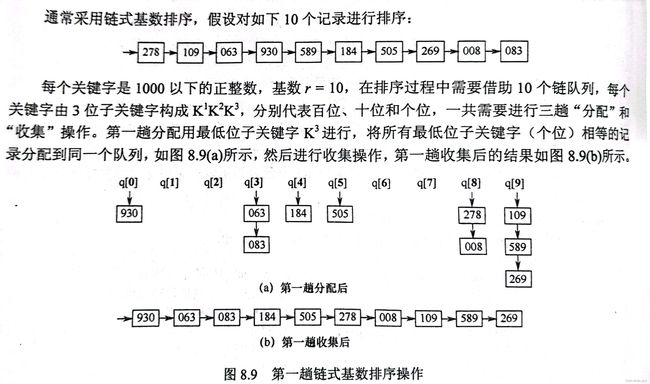
我们需要创建一个q[0]~q[9]的收集链队，将所有数字视为其中的最高位数，在这里是三位数，那么我们依次以个十百位进行收集
第一趟我们按照个位分配，得到的链队如（a）所示，然后将其顺序相连形成了链队（b）

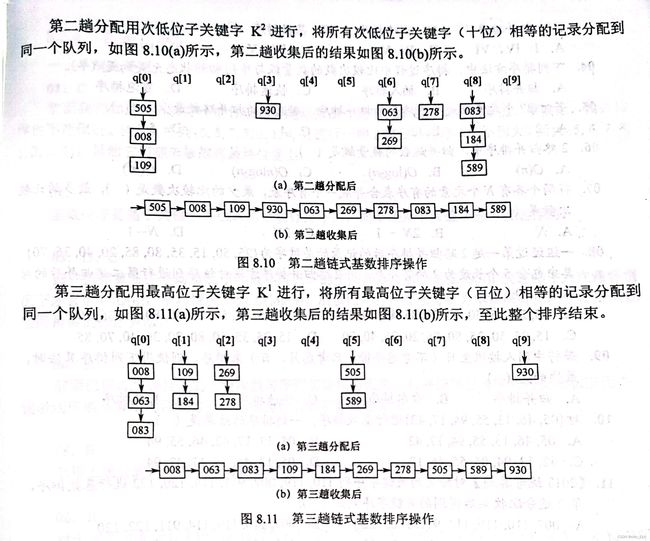
第二次第三次分别分配十，百位
当最后一位分配完毕我们可以看到得到了一个降序序列
理论上来说从百位开始分配收集是更好的选择
基数排序是一种稳定的排序法

---

内部排序算法的比较

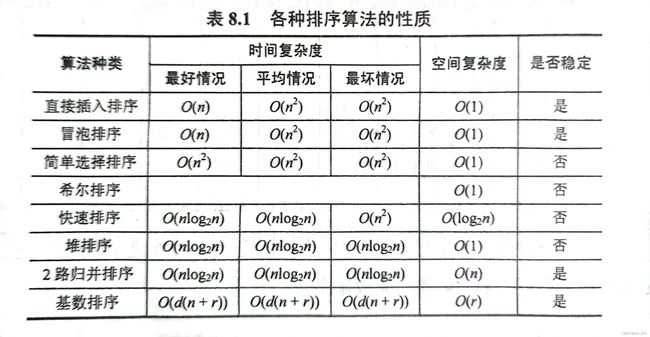
由于希尔排序取决于其内部的增量函数（查找方式），因此无法比较

---

外部排序

上述的内部排序算法其排序方法都是在内存中进行的，由于某些文件很大，无法完全放在内部进行排序。
外部排序算法可以将当前排序元素放在内存，把等待排序元素放在外存，在排序时进行内存和外存间的元素交换，实现整体的排序。

二路归并

外部排序的一个经典算法就是二路归并

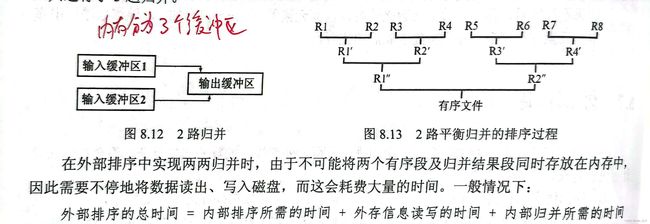
首先我们简单地把内存分为三块：输入缓冲区1，输入缓冲区2，输出缓冲区。（缓冲区即buffer）
由于一个单线程程序执行二路归并的过程，就是将两个输入归并为一个输出，因此实际上3个缓冲区就够用了
在这一例子中，R1~R8都存储于外存，我们从外存中取到R1R2放入内存输入缓冲区，二者归并到输出缓冲区，我们再将输出缓冲区的内容输出到外存的R1’中，如此实现内存和外存的交替
图8.13每一层代表一趟归并排序，总共经历了三趟排序
但是由于内外存交替存取，实际上依靠是的磁盘I/O操作，因此有很多时间会花在IO操作上，因此尽可能减少IO操作可以有效减少外部排序的总时间

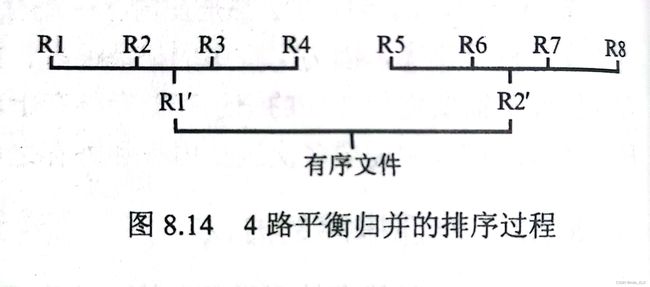
多路归并就少了一趟归并递归，因此IO操作量也少了

---

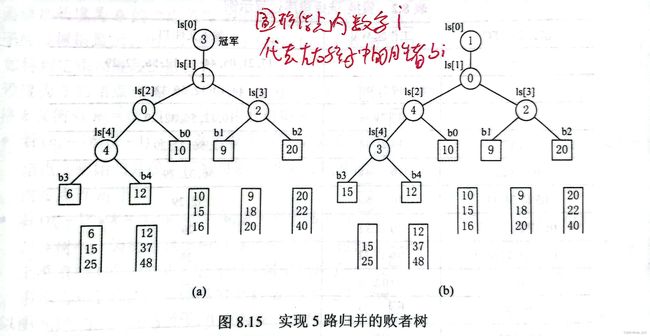
败者树

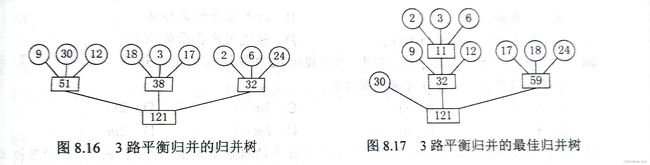
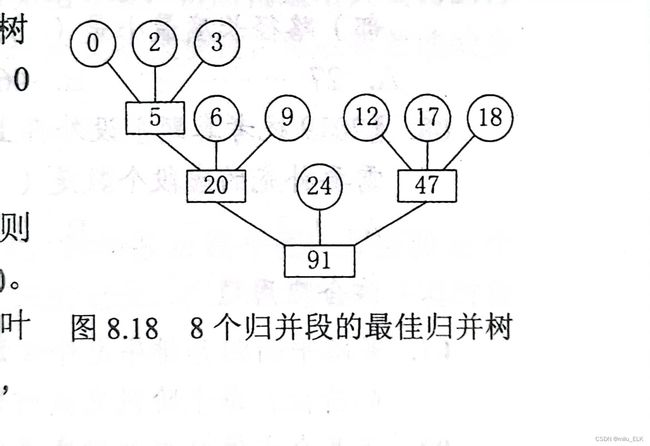
多路归并虽然能有效减少IO次数，（以 k 路归并为例），但是有一个问题，就是随着 k 的增加，在归并内部花费的时间反而会越来越多，这样时间上反而得不偿失。
因此我们引入败者树，败者树是树形选择排序的一种变体，可以视为一颗完全二叉树。
k 个叶结点分别存放在k 个归并段在归并过程中当前参加比较的记录
除了叶子结点外的内部结点用于记忆左右子树中的“失败者”，胜者往上比较，一直达到根结点成为“冠军”
例如下列例子中我们以小的数为胜利者，根节点则为最小数，反之根节点为最大数

---

最佳归并树

最佳归并树其实就是一个倒过来的 k 叉哈夫曼树
IO次数=2*WPL