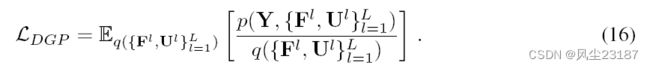论文笔记Doubly Stochastic Variational Inference for Deep Gaussian Processes深度高斯过程的双重随机变分推理

0. 摘要

高斯过程 (GP) 是函数逼近的一个不错的选择，因为它们灵活、对过度拟合具有鲁棒性，并提供经过良好校准的预测不确定性。 深度高斯过程 (DGP) 是 GP 的多层泛化，但事实证明这些模型中的推理具有挑战性。 DGP 模型中现有的推理方法假设近似后验，迫使各层之间独立，并且在实践中效果不佳。 我们提出了一种双随机变分推理算法，该算法不强制层之间的独立性。 通过我们的推理方法，我们证明了 DGP 模型可以有效地用于大小从数百到十亿点的数据。 我们提供了强有力的经验证据，证明我们的 DGP 推理方案在分类和回归的实践中都能很好地工作。

1. 介绍

高斯过程 (GP) 在包括机器人技术 (Ko and Fox, 2008; Deisenroth and Rasmussen, 2011)、地质统计学 (Diggle and Ribeiro, 2007)、数字学 (Briol et al. , 2015)、主动传感 (Guestrin et al., 2005) 和优化 (Snoek et al., 2012)。高斯过程由其均值和协方差函数定义。在某些情况下，先验知识可以很容易地结合到这些功能中。示例包括气候建模中的周期性（Rasmussen 和 Williams，2006 年）、时间序列数据中的变化点（Garnett 等人，2009 年）和机器人模拟器先验（Cutler 和 How，2015 年）。在其他设置中，GP 成功地用作黑盒函数逼近器。即使对数据知之甚少，使用 GP 也有令人信服的理由：GP 的复杂性不断增加以适应数据； GP 对过度拟合具有鲁棒性，同时提供合理的预测误差条； GP 可以用很少的超参数对丰富的函数类别进行建模。

单层 GP 模型受到核/协方差函数的表达能力的限制。在某种程度上，可以从数据中学习内核，但是在大且参数化的内核空间上进行推理是昂贵的，并且近似方法可能存在过度拟合的风险。仅当超参数的数量很少时，关于超参数的边际似然优化才近似于贝叶斯推理（Mackay，1999）。例如，尝试使用高度参数化的神经网络作为核函数（Calandra 等人，2016 年；Wilson 等人，2016 年）会导致深度学习的缺点，例如需要特定于应用程序的架构和正则化技术.内核可以通过求和和乘积进行组合（Duvenaud 等人，2013），以创建更具表现力的组合内核，但这种方法仅限于简单的基础内核，而且它们的优化成本很高。

深度高斯过程 (DGP) 是 GP 的分层组合，可以克服标准（单层）GP 的局限性，同时保留其优势。 DGP 是比标准 GP 更丰富的模型，正如深度网络比广义线性模型更丰富一样。与具有高度参数化内核的模型相比，DGP 以非参数方式学习表示层次结构，只需要很少的超参数进行优化。

与单层 gp 不同，DGP 已被证明难以训练。先前工作中使用的平均场变分方法（Damianou 和 Lawrence，2013；Mattos 等人，2016；Dai 等人，2016）做出了很强的独立性和高斯假设。真正的后验可能在层之间表现出高度相关性，但众所周知，平均场变分方法严重低估了这些情况下的方差（Turner 和 Sahani，2011 年）。

在本文中，我们提出了一种用于在 DGP 模型中进行推理的变分算法，该算法不强制层之间的独立性或高斯性。与许多最先进的 GP 近似方案一样，我们从稀疏诱导点变分框架 (Matthews et al., 2016) 开始，以实现每一层内的计算易处理性，但我们不强制层之间的独立性。相反，我们使用以诱导点为条件的精确模型作为变分后验。该后验与完整模型具有相同的结构，特别是它保持了层之间的相关性。由于我们在变分后验中保留了完整模型的非线性，因此我们失去了分析的易处理性。我们通过从变分后验采样克服了这个困难，引入了随机性的第一个来源。由于稀疏变分后边缘的一个重要特性，这在计算上很简单：以下层为条件的边缘仅取决于相应的输入。因此，可以在不计算层内的全协方差的情况下获得来自顶层边缘的样本。我们主要对大数据应用感兴趣，因此我们进一步对小批量数据进行二次抽样。随机性的第二个来源使我们能够扩展到任意大的数据。

我们通过大量实验证明我们的方法在实践中效果很好。我们提供了关于基准回归和分类数据问题的结果，并且还展示了第一个 DGP 应用到具有十亿个点的数据集。我们的实验证实，DGP 模型永远不会比单层 GP 差，而且在许多情况下要好得多。至关重要的是，我们展示了额外的层不会导致过度拟合，即使是小数据。

2. 背景

2.1 单层GPs

高斯过程由后验分布$f:R^D\to R$定义
N个输入$x=\{x_1,...,x_N\}$
N个输出$y=\{y_1,...,y_N\}$
似然函数:$p(y|f)$
在高斯过程模型下，假定$f=f(x)$是联合高斯且协方差函数为$k:R^D\times R^D\to R$，均值函数为 $m：R^D\to R$ ，其中,$f(x)=\{f(x_1),...,f(x_N)\}$。我们进一步定义额外的 $M$ 个诱导位置 $Z=(z_1,...,z_M{)}^T$,我们使用 $f=f(x),u=f(z)$ 代表设计点和诱导点的函数值，使用 $[m(X){]}_i=m(x_i),[k(X,Z){]}_{ij}=k(x_i,z_j)$ 定义。根据 GP 的定义，联合密度 $p(f,u)$ 是一个高斯，其均值由在每个输入 $(X,Z{)}^T$ 处评估的均值函数给出，相应的协方差由在每对输入评估的协方差函数给出。 $y,f,u$ 的联合密度是
$$p(y,f,u)=\underset{GPprior}{p(f|u;X,Z)p(u;Z)}\underset{likehood}{\prod _{i=1}^{N}p(y_i|f_i)}\text{\hspace{1em}(1)}$$

在 (1) 中，我们将联合 GP 先验 $p(f,u;X,Z)$ 分解为先验 $p(u)=N(u|m(Z),k(Z;Z))$ 和条件 $p(f|u;X,Z)=N(f|\mu ,\Sigma )$, 其中对于 $i，j=1,...,N$
$$[\mu {]}_i=m(x_i)+\alpha (x_i{)}^T(u-m(Z))\text{\hspace{1em}(2)}$$
$$[\Sigma {]}_{ij}=k(x_i,x_j)-\alpha (x_i{)}^{T}k(Z,Z)\alpha (x_j)\text{\hspace{1em}(3)}$$
（在本文中，我们使用分号表示法来阐明相应函数值的输入位置，这将在我们稍后讨论多层 GP 模型时变得重要。 例如，$p(f|u;X,Z)$ 表示 $f$ 和 $u$ 的输入位置分别是 $X$ 和 $Z$。）

$\alpha (x_i)=k(Z,Z{)}^{-1}k(Z,x_i)$。 请注意，分别通过 (2) 和 (3) 定义的条件均值 $\mu$ 和协方差 $\Sigma$ 采用输入 $x_i$ 的均值和协方差函数的形式。 当似然 $p(y|f)$ 为高斯时，模型 (1) 中的推理可能以封闭形式进行，但计算与 N 成三次方。

我们对具有非高斯似然的大型数据集感兴趣。 因此，我们寻求变分后验来同时克服这两个困难。 变分推理通过最小化变分后验 $q$ 和真实后验 $p$ 之间的 Kullback-Leibler 散度 $KL[q||p]$ 来寻求近似后验 $q(f,u)$。 等效地，我们最大化边际似然（证据）的下限
$$L=E_{q(f,u)}[\log \frac{p(y,f,u)}{q(f,u)}]\text{\hspace{1em}(4)}$$
其中 $p(y,f,u)$在式1中给出，我们按照 Hensman 等人（2013）并选择变分后验
$$q(f,u)=p(f|u;X,Z)q(u)\text{\hspace{1em}(5)}$$
其中 $q(u)=N(u|m,S)$。由于变分后验中的两个项都是高斯的，我们可以分析地边缘化 $u$，从而产生
$$q(f|m,S;X,Z)=\int p(f|u;X,Z)q(u)du=N(f|\tilde{\mu },\tilde{\Sigma })\text{\hspace{1em}(6)}$$
与 (2) 和 (3) 类似，$\tilde{\mu }$ 和 $\tilde{\Sigma }$ 的表达式可以写成输入的均值和协方差函数。 为了强调这一点，我们定义
$${\mu }_{m,Z(x_i)}=m(x_i)+\alpha (x_i{)}^T(m-m(z))\text{\hspace{1em}(7)}$$
$${\Sigma }_{S,Z(x_i,x_j)}=k(x_i,x_j)-\alpha (x_i{)}^T(k(Z,Z)-S)\alpha (x_j)\text{\hspace{1em}(8)}$$

通过这些函数，我们定义了 $[\tilde{\mu }{]}_i={\mu }_{m,Z(x_i)}$ 和 $[\tilde{\Sigma }{]}_{ij}={\Sigma }_{S,Z(x_i,x_j)}$。 我们以这种方式编写了均值和协方差，以使以下观察清楚。

备注 1.: 变分后验 (6) 的 $f_i$ 边际仅取决于相应的输入 $x_i$ 。 因此，我们可以将 $q(f|m,S;X,Z)$ 的第 $i$个边缘写成
$$q(f_i|m,S;X,Z)=q(f_i|m,S;x_i,Z)=N(f_i|{\mu }_{m,Z(x_i)},{\Sigma }_{S,Z(x_i,x_j)})\text{\hspace{1em}(9)}$$
使用我们的变分后验 (5) 下限 (4) 大大简化了，因为 (a) 对数内的条件 $p(f|u;X;Z)$ 取消和 (b) 似然期望只需要变分边缘。 我们获得
$$L=\sum _{i=1}^N{E}_{q(f_i|m,S;x_i,Z)}[\log p(y_i|f_i)]-KL[q(u)||p(u)]\text{\hspace{1em}(10)}$$

在某些情况下，对数似然的最终（单变量）期望可以通过正交（Hensman 等人，2015 年）或通过蒙特卡罗抽样（Bonilla 等人，2016 年；Gal 等人，2015 年）进行分析计算。由于边界是数据的总和，因此可以通过小批量子采样获得无偏估计量。这允许对大型数据集进行推断。在这项工作中，我们将具有这种推理方法的 GP 称为稀疏 GP (SGP)。

通过最大化下限 (10) 找到变分参数$（Z、m和S）$。由于 $L$ 是边际似然 $p(y|X)$ 的下限，因此保证了该最大化收敛。我们还可以通过最大化这个界限来学习模型参数（内核的超参数或似然性），尽管我们应该谨慎行事，因为这会引入偏差，因为对于所有超参数设置，界限并不是一致严格的（Turner 和 Sahani，2011）

所以到目前为止，我们已经考虑了标量输出 $y_i\in \mathbb{R}$。在 D 维输出 $y_i\in {\mathbb{R}}^D$ 的情况下，我们将 $Y$ 定义为第 $i$ 行包含第 $i$ 个观测值 $y_i$ 的矩阵。类似地，我们定义 $F$ 和 $U$ 。如果每个输出是一个独立的 GP，我们有 GP 先验 ${\prod }_{d=1}^{D}p(F_d|U_d;X,Z)p(U_d;Z)$，我们将其缩写为 $p(F|U;X,Z)p(U;Z)$ 以减轻符号。

2.2 深度GPs

DGP (Damianou and Lawrence, 2013) 在向量值随机函数 $F^1,...,F^L$ 上递归地定义了先验。每个函数 $F^l$ 的先验是每个维度上的独立 GP，输入位置由下一层函数值的噪声损坏给出：第 $l$ 层 $GP$ 的输出是 $F_d^l$，对应的输入是 $F^{l-1}$ .假设层之间的噪声 i.i.d.高斯。 DGP 的大多数介绍（参见，例如 Damianou 和 Lawrence，2013 年；Bui 等人，2016 年）明确地将噪声损坏与每个 GP 的输出分开参数化。我们的推理方法不需要我们单独参数化这些变量。因此，为了符号方便，我们将噪声吸收到内核中 $k_{noisy}(x_i,x_j)=k(x_i,x_j)+{\sigma }_l^2{\delta }_{ij}$，其中 ${\delta }_{ij}$ 是 Kronecker delta，${\sigma }_l^2$ 是层间的噪声方差.我们使用 $D^l$ 作为第 $l$ 层输出的维度。与单层情况一样，我们在每一层都有诱导位置 $Z^{l-1}$ 和每个维度的诱导函数值 $U^l$。

过程的实例化具有联合密度
$$p(Y,\{F^l,U^l{\}}_{l=1}^L)=\underset{likehood}{\prod _{i=1}^{N}p(y_i|f_i^L)}\underset{DGPprior}{\prod _{l=1}^{L}p(F^l|U^l;F^{l-1},Z^{l-1})}\text{\hspace{1em}(11)}$$

我们定义 $F^0=X$。在这个模型中推断是难以处理的，所以必须使用近似值。

最初的 DGP 演示文稿（Damianou 和 Lawrence，2013 年）使用变分后验来维持以 $U^l$ 为条件的精确模型，但进一步强制每一层的输入独立于前一层的输出。噪声损坏被单独参数化，并且这些变量的变分分布是完全分解的高斯分布。这种方法需要 $2N(D^1+...+D^{L-1}$) 个变分参数，但如果内核具有特定形式，则允许对数边际似然有一个易于处理的下限。该界限的另一个问题是输出上的密度只是具有独立高斯输入的单层 GP。由于后验失去了层之间的所有相关性，它不能表达完整模型的复杂性，因此可能会低估方差。在实践中，我们发现在 Damianou 和 Lawrence (2013) 中优化目标会导致层被“关闭”（信噪比趋于零）。相比之下，我们的后验保留了真实模型的完整条件结构。我们牺牲了分析的易处理性，但由于每一层内的稀疏后验，我们可以使用单变量高斯对边界进行采样。

3. 双随机变分推理

在本节中，我们提出了一种新的变分后验，并演示了一种从得到的下限中获得无偏样本的方法。 推断 DGP 模型的困难在于层内和层之间存在复杂的相关性。 我们的方法很简单：我们使用稀疏变分推理来简化层内的相关性，但我们保持层之间的相关性。 由此产生的变分下限无法进行分析评估，但我们可以使用单变量高斯有效地绘制无偏样本。 我们随机优化我们的界限。

我们提出了具有三个属性的后验。 首先，后验保持精确的模型，以 $U^l$ 为条件。 其次，我们假设 $\{U^l{\}}_{l=1}^L$ 的后验分布在层（和维度，但我们从符号中抑制）之间分解。 因此，我们的后验采用简单的因式分解形式:
$$q(\{F^l,U^l{\}}_{l=1}^L)=\prod _{l=1}^{L}p(F^l|U^l;F^{l-1},Z^{l-1})q(U^l)\text{\hspace{1em}(12)}$$

第三，为了完成后验的说明，我们将 $q(U^l)$ 设为具有均值 $m^l$ 和方差 $S^l$ 的高斯分布。 Hensman and Lawrence (2014) 和 Dai 等人使用了类似的后验。 (2016)，但这些工作中的每一个都包含针对每一层的噪声损坏的附加术语。 与单层 SGP 一样，我们可以分析地边缘化来自每一层的诱导变量。 在这种边缘化之后，我们得到以下分布，它在层内和层之间完全耦合：
$$q(\{F^l{\}}_{l=1}^L)=\prod _{l=1}^{L}q(F^l|m^l;F^{l-1},Z^{l-1})=\prod _{l=1}^{L}N(f^l|{\tilde{\mu }}^l,{\tilde{\Sigma }}^l)\text{\hspace{1em}(13)}$$
其中，$q(F^l|m^l;F^{l-1},Z^{l-1})$如等式6所示。具体来说它是 $N({\tilde{\mu }}^l,{\tilde{\Sigma }}^l)$,且$[{\tilde{\mu }}^l{]}_i={\mu }_{m^l.Z^{l-1}}(f_i^l,f_j^l)$（回想一下，$f_i^l$ 是 $F^l$ 的第 $i$ 行）。由于 公式(12) 是每一项都采用 SGP 变分后验 (5) 形式的项的乘积，我们再次具有这样的性质，即在每一层内，边际仅取决于相应的输入。 特别是，$f_i^L$ 仅取决于 $f_i^{L-1}$ ，而 $f_i^{L-1}$ 又仅取决于 $f_i^{L-2}$ ，依此类推。 因此，我们有以下性质：
备注 2. 变分 DGP 后验 (12) 的最后一层的第 $i$ 个边缘仅取决于所有其他层的第 $i$ 个边缘。 即
$$q(f_i^L)=\int \prod _{l=1}^{L}q(F_i^l|m^l;F_i^{l-1},Z^{l-1})d{f}_i^l\text{\hspace{1em}(14)}$$
该属性的结果是从 $q(f_i^L)$ 中抽取样本很简单，此外，我们可以使用“重新参数化技巧”（Rezende et al., 2014; Kingma et al. ., 2015)。 具体来说，我们首先对${ϵ}_i^l$~ $N(0,I_{D^l})$ 进行采样，然后递归得到采样变量${\hat{f}}_i^l$~$q(F_i^l|m^l;F_i^{l-1},Z^{l-1})$$l=1,...,L-1$,即

$${\hat{f}}_i^l={\mu }_{m^l,Z^{l-1}}({\hat{f}}_i^{l-1})+{ϵ}_i^l⨀\sqrt{{\Sigma }_{S^l,Z^{l-1}}({\hat{f}}_i^{l-1},{\hat{f}}_i^{l-1})}\text{\hspace{1em}(15)}$$

其中 (15) 中的项是 $D^l$ 维的，平方根是元素方面的。 对于第一层，我们定义${\hat{f}}_i^0:=x_i$。

证据下限的有效计算
DGP 的证据下界是

将(11)和(12)对(16)中的对应表达式进行一些重新排列后得到

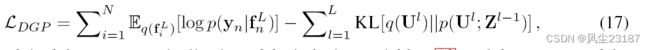
我们利用了诱导变量 (13) 的精确边缘化和最后一层 (14) 的边缘属性。 补充材料中提供了详细的推导。 这个界限的复杂度为 $O(N{M}^2(D^1+...+D^L))$ 来评估。 我们使用两个随机源来近似评估界限（17）。 首先，我们用来自变分后验（14）的蒙特卡罗样本来近似期望，我们根据（15）计算。 由于我们已经根据各向同性高斯参数化了这个采样过程，我们可以计算边界的无偏梯度（17）。 其次，由于边界分解了数据，我们通过对数据进行二次采样来实现可扩展性。 两种随机近似都是无偏的。

预测
为了预测，我们从将输入位置更改为测试位置 $x_{\ast }$ 的变分后验进行采样。 我们将测试位置的函数值表示为 $f_{\ast }^L$ 。 为了获得 $f_{\ast }^L$ 上的密度，我们使用高斯混合

我们使用 (15) 绘制 S 个样本 $f_{\ast }^{(s{)}^{L-1}}$，但将输入 $x_i$ 替换为测试位置 $x$ 。

进一步的模型细节

虽然 GP 通常与零均值函数一起使用，但我们认为这种选择不适合 DGP 的内层。 使用零均值函数会导致 DGP 先验困难，因为每个 GP 映射都是高度非内射的。 Duvenaud 等人分析了这种效应。 (2014) 作者建议将原始输入 X 添加到每一层。 相反，我们考虑另一种方法，并为所有内层包括一个线性平均函数 m(X) = XW。 如果输入和输出维度相同，我们使用 W 的单位矩阵，否则我们计算数据的 SVD 并使用按奇异值排序的顶部 $D^l$ 左特征向量（即 PCA 映射）。 通过这些选择，初始化所有诱导平均值 $m^l=0$ 是有效的。平均函数的这种选择部分受到 ResNet（He 等人，2016）架构的“跳过层”方法的启发。

4. 结论

我们在许多基准回归和分类数据集上评估我们的推理方法。 我们强调，我们对可以在小型和大型数据体系中运行的模型感兴趣，几乎不需要手动调整。 我们所有的实验都使用完全相同的超参数和初始化运行。 有关详细信息，请参阅补充材料。 我们对 DGP 模型的所有内层使用 $min(30;D^0)$，其中 D0 是输入维度，所有层都使用 RBF 内核。

回归Benchmarks
我们在 8 个标准中小型 UCI 基准数据集上将我们的方法与其他最先进的方法进行比较。按照惯例（例如 Hernández-Lobato 和 Adams，2015），我们使用 20 倍交叉验证和 10% 随机选择的保留测试集，并将输入和输出缩放到训练集中的零均值和单位标准差（我们恢复用于评估的输出缩放）。虽然我们可以使用任何内核，但我们为每个维度选择具有长度尺度的 RBF 内核，以便与 Bui 等人进行直接比较（2016 年）。测试对数似然结果如图 1 所示。

我们比较了 2、3、4 和 5 层（DGP 2-5）的模型，每个模型有 100 个诱导点，具有（随机优化的）稀疏 GP（Hensman 等人., 2013) 具有 100 和 500 个诱导点 (SGP, SGP 500)。我们还与具有 ReLu 激活、50 个隐藏单元（蛋白质和年份分别为 100 个）的两层贝叶斯神经网络进行了比较，通过概率反向传播进行推断（Hernández-Lobato 和 Adams，2015）（PBP）。结果取自 Hernández-Lobato 和 Adams (2015)，并被发现是其他几种推断贝叶斯神经网络的方法中最有效的。我们还与具有近似期望传播 (EP) 的 DGP 模型进行了比较（Bui et al., 2016）。使用作者的代码 2，我们使用近似期望传播 (Bui et al., 2016) (AEPDGP 2) 运行了一个具有 1 个隐藏层的 DGP 模型。我们使用隐藏层的输入维度与我们的模型进行公平比较3(3 然而，我们注意到在 Bui 等人中, (2016) 内层是二维的，因此我们获得的结果与 Bui 等人报道的结果不能直接比较。 (2016))。我们发现用这种推理训练 3 层模型的时间要求令人望而却步。可以在补充材料中找到测试 RMSE 的图和进一步的结果表。

在八个数据集中的五个上，最深的 DGP 模型是最好的。 在“wine”、“naval”和“boston”上，我们的 DGP 恢复了单层 GP，这并不奇怪：“boston”非常小，“wine”接近线性（注意线性模型和 规模）和“海军”的特点是极高的测试似然性（对于所有 SGP 和 DGP 模型，该数据集上的 RMSE 小于 0.001），即它对于 GP 来说是一个非常“简单”的数据集。 对于任何数据集，贝叶斯网络都不比稀疏 GP 好，而对于 6 个数据集则明显更差。 对于许多数据集，DGP 模型的近似 EP 推理也无法与稀疏 GP 竞争，但这可能是因为初始化是为比我们使用的更低维隐藏层设计的。

我们在这些中小型数据集上的结果证实，DGP 模型没有观察到过度拟合，并且 DGP 永远不会比单层 GP 更差，而且通常更好。 我们特别注意到，在“功率”、“蛋白质”和“kin8nm”数据集上，所有 DGP 模型的性能都优于 SGP，其诱导点数是 SGP 的五倍。

Rectangles Benchmark
我们使用 Rectangle-Images 数据集4，该数据集专门用于区分深层和浅层架构。 该数据集包含 12,000 个训练示例和 50,000 个测试示例，大小为 $28\times 28$，其中每个图像都由一个（非正方形）矩形图像与不同背景图像组成。 任务是确定高度和宽度中的哪一个最大。 我们运行 2、3 和 4 层 DGP 模型，并观察到每一层的性能都在提高。 表 1 包含结果。 请注意，500 个诱导点单层 GP 的效果明显低于任何深度模型。 我们的 4 层模型达到了 77.9% 的分类准确率，超过了 Larochelle 等人报告的 77.5% 的最佳结果（2007）具有三层深度信念网络。 我们也超过了 Krauth 等人报告的 76.4% 的最佳结果。 (2016) 使用带有反正弦核、留一目标和 1000 个诱导点的稀疏 GP。

大规模回归
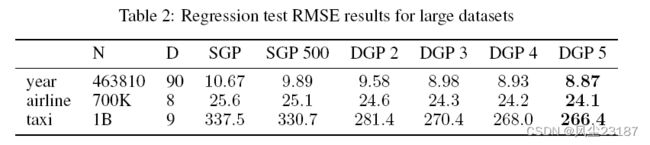
为了展示我们在大规模回归问题上的方法，我们使用了 UCI 的“年份”数据集和“航空公司”数据集，它们已被大规模 GP 社区普遍使用。 对于“航空公司”数据集，我们将前 700K 点用于训练，然后将 100K 点用于测试。 我们对“年份”数据集使用 10% 的随机拆分。 结果如表 2 所示，补充材料中报告了对数似然。 在这两个数据集中，我们看到 DGP 模型随着深度的增加表现更好，在对数似然和 RMSE 方面都比单层模型显着提高，即使有 500 个诱导点。

MNIST 多类分类
我们将具有 2 层和 3 层的 DGP 应用于 MNIST 多类分类问题。我们使用鲁棒最大多类似然性 (Hernández-Lobato et al., 2011)，并使用标准训练/测试分割为 60K/10K 的完整未处理数据。具有 100 个诱导点的单层 GP 的测试准确率达到 97.48%，而两层和三层 DGP 分别提高到 98.06% 和 98.11%。 500 个诱导点单层模型在我们的实现中达到了 97.9%，尽管之前曾报道该模型的结果略高，分别为 98.1%（Hensman 等人，2013 年）和 98.4%（Krauth 等人，2016 年）。同型号有1000个感应点。我们将这种差异归因于不同的超参数初始化和训练计划，并强调我们对所有模型使用完全相同的初始化和学习计划。对于具有二维潜在空间的两层模型，该数据集文献中唯一的其他 DGP 结果是 94.24%（Wang 等人，2016 年）。

大规模分类
我们使用 HIGGS (N = 11M, D = 28) 和 SUSY (N = 5:5M, D = 18) 数据集进行大规模二元分类。这些数据集是根据蒙特卡罗物理模拟构建的，以检测希格斯玻色子和超对称性的存在（Baldi 等人，2014 年）。我们抽取 10% 的随机样本进行测试，其余的用于训练。我们使用 AUC 指标与 Baldi 等人进行比较。 （2014）。与浅层神经网络 (NN, 0.875)、深度神经网络 (DNN, 0.876) 和增强决策树 (BDT, 0.863) 相比，我们的 DGP 模型在 SUSY 数据集（所有 DGP 模型的 AUC 为 0.877）上性能最高。在 HIGGS 数据集上，我们看到附加层的稳步改进（DGP 2-4 分别为 0.830、0.837、0.841 和 0.846）。在这个数据集上，DGP 模型的性能超过了 BDT (0.810) 和 NN (0.816) 以及单层 GP 模型 SGP (0.785) 和 SGP 500 (0.794)。该数据集上表现最好的模型是 5 层 DNN (0.885)。完整的结果报告在补充材料中。

大规模回归
为了证明我们的模型在海量数据上的有效性，我们使用了纽约市黄色出租车出行数据集，该数据集包含 12.1 亿次行程 数据集。继 Peng 等人之后。 (2017) 我们使用 9 个特征：一天中的时间；一周中的天;一个月中的哪一天；月;接送经纬度；下车经纬度；行驶距离。目标是预测行程时间。我们随机选择 1B (109) 个示例进行训练并使用 1M 个示例进行测试，并且我们将训练数据中的输入和输出都缩放到零均值和单位标准差。我们丢弃小于 10 秒或大于 5 小时的旅程，或在纽约地区以外开始/结束的旅程，我们估计距离纽约中心的平方距离小于 $5^o$。测试 RMSE 结果是表 2 的底行，测试日志可能性在补充材料中。我们注意到从单层模型到 DGP 的性能显着提升。与所有大规模实验一样，我们看到额外层的持续改进，但在这个数据集上，改进特别引人注目（与 SGP 相比，DGP 5 的 RMSE 降低了 21%）

5.相关工作

一个 GP 的输出用作另一个 GP 的输入的第一个例子可以在 Lawrence and Moore (2007) 中找到。 MAP近似用于推理。 Titsias 和 Lawrence (2010) 的开创性工作展示了如何使用稀疏变分推理通过具有高斯似然性的 GP 传播高斯输入。这种方法在 Damianou 等人中得到了扩展。 （2011 年）在 Lawrence 和 Moore（2007 年）的模型中进行近似推理，不久之后在类似的模型 Lázaro-Gredilla（2012 年）中进行了近似推理，该模型还包括线性均值函数。这两种方法的关键思想是层间变分后验的因式分解。一个更通用的模型（隐藏层的深度和维度灵活）引入了术语“DGP”并使用了也在层之间分解的后验。这些方法需要在数据数量中线性增加数量的变分参数。对于高维观察，可以使用辅助模型来分摊这种优化的成本。 Dai 等人采用了这种方法。 （2016），并在 Mattos 等人中使用了一个循环架构。 （2016 年）。 Hensman 和 Lawrence (2014) 提出了在精确模型中进行推理的另一种方法，其中 GP 输出在层内使用了稀疏近似，类似于 Damianou 和 Lawrence (2013)，但在输入的预测分布下一层。选择变分分布的特定形式是为了接受一个易于处理的界限，但对灵活性施加了约束。

另一种方法是直接修改 DGP 先验并在参数模型中执行推理。这是在 Bui 等人中实现的。 （2016）在每一层内都有一个诱导点近似，在 Cutajar 等人中。 （2017）与内核的频谱密度近似。然后，两种方法都应用额外的近似值来实现易于处理的推理。在 Bui 等人。 (2016)，使用期望传播的近似值，对对数分区函数附加高斯近似值，以通过非线性 GP 映射不确定地传播。在 Cutajar 等人中。 （2017）对光谱分量使用完全分解的变分近似。这两种方法都需要特定的内核：在 Bui 等人中。 （2016）内核必须在高斯下具有分析期望，并且在 Cutajar 等人中。 (2017) 内核必须具有解析谱密度。 Vafa (2016) 也使用与 Bui 等人相同的初始近似值。 (2016) 但对诱导点应用 MAP 推断，这样通过层传播的不确定性仅代表近似的质量。在无限多个诱导点的限制下，这种方法恢复了确定性径向基函数网络。 Wang等人使用了粒子方法。 (2016)，再次使用 Bui 等人使用的稀疏近似的在线版本。 （2016）在每一层内。与我们的方法类似，在 Wang 等人中。 (2016) 样本是通过条件模型获取的，但与我们不同的是，它们随后对潜在变量使用点估计。目前尚不清楚这种方法如何通过层传播不确定性，因为每一层的 GP 都有点估计输入和输出。

Duvenaud 等人确定了内层平均函数为零的 DGP 病理学。 （2014）。在 Duvenaud 等人。 (2014) 提出了在每一层连接原始输入的建议。 Dai 等人采用了这种方法。 (2016) 和 Cutajar 等人。 （2017）。线性均值函数最初由 Lázaro-Gredilla (2012) 使用，尽管在具有一维隐藏层的两层 DGP 的特殊情况下。据我们所知，以前没有尝试对所有内层使用线性平均函数。

6. 讨论

我们的实验表明，在广泛的任务中，具有双重随机推理的 DGP 模型既有效又可扩展。至关重要的是，我们观察到，在小数据集上，DGP 不会过拟合，而在大数据集上，附加层通常会提高性能并且不会降低性能。特别是，我们注意到随着层数的增加，最大的增益是在最大的数据集（出租车数据集，有 1B 个点）上实现的。我们还注意到，在所有大规模实验中，SGP 500 模型的表现都优于所有 DGP 模型。因此，对于相同的计算预算，增加层数比增加单层模型中近似推理的准确性要有效得多。除了相当适中的额外计算时间（见表 3）之外，我们没有看到使用 DGP 而不是单层 GP 的缺点，但有很大的优势。

虽然我们考虑了简单的内核和黑盒应用程序，但任何特定领域的内核都可以在任何层中使用。这与需要特定内核和复杂实现的其他方法（Damianou 和 Lawrence，2013 年；Bui 等人，2016 年；Cutajar 等人，2017 年）形成鲜明对比。我们的实现很简单（< 200 行），公开可用的 6 行，并与 GPflow（Matthews 等人，2017 年）集成，这是一个建立在 Tensorflow 之上的开源 GP 框架（Abadi 等人，2015 年）。

7. 结论

我们提出了一种在深度高斯过程 (DGP) 模型中进行推理的新方法。 通过我们的推断，我们已经表明 DGP 可以用于一系列回归和分类任务，而无需手动调整。 我们的结果表明，在实践中，DGP 总是超过或匹配单层 GP 的性能。 此外，我们已经证明 DGP 经常显着超过单层，即使单层的近似质量得到了提高。 我们的方法具有高度可扩展性，并受益于 GPU 加速。 我们的方法最重要的限制是处理高维内层。 我们对高维数据集使用了线性平均函数，但这个平均函数是固定的，因为优化参数会违背我们的非参数范式。 根据 Titsias 和 Lázaro-Gredilla (2013) 的工作，可以概率地处理这种映射。