[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)
第一作者:Sundar Vedula
发表时间:1999
论文链接:https://ieeexplore.ieee.org/abstract/document/790293
Three-Dimensional Scene Flow
摘要:
场景流是世界上点的三维运动场,就像光流是图像中点的二维运动场一样。任何光流都只是场景流在相机像平面上的投影。在本文中,我们提出了一个从光流计算稠密、非刚性场景流的框架。我们的方法为简单的线性算法,并将任务分类为三个主要场景:( 1 )完整的场景结构的瞬时知识,( 2 )仅有对应信息的知识,( 3 )没有场景结构的知识。我们还表明,在没有某种形式的平滑或正则化的情况下,无法直接使用正常流的多个估计来估计稠密场景流。
1、引言:
光流是图像平面内的二维运动场。它是世界三维运动的投影。如果世界是完全非刚性的,场景中各点的运动可能都是相互独立的。因此,场景运动的一种表示方式是为场景中每个表面上的每个点定义一个稠密的三维向量场。类比光流,我们将这种三维运动场称为场景流。在本文中,我们提出了一个直接从光流计算稠密、非刚性场景流的框架。我们的方法导致了高效的线性算法和任务的三个主要场景的分类:
1、完整的场景结构的瞬时知识,包括表面法线和深度图的变化率。在这种情况下,只需要一个光流来计算场景流。
2、只知道立体对应关系。在这种情况下,至少需要两个光流来计算场景流,但更多的是提高鲁棒性。
3、没有表面的知识。在这种情况下,可以在一个重建算法中使用多个光流来估计场景结构(然后是场景流)。
针对每个场景,我们提出了一种算法,并在一个动态、非刚性场景的视频序列集合上进行了演示。我们还表明,在没有某种形式的正则化或平滑的情况下,无法直接使用正常流的多个估计来估计场景流。
场景流的一个可能应用是作为高效和鲁棒的立体预测器。给定场景在某一时刻的重建模型,人们希望在下一个时间步使用最小的计算量获得结构的估计。这将允许:( 1 )在下一个时间步长可以更有效地计算结构,因为得到的第一个估计值可以减少接下来的搜索空间;( 2 )更鲁棒的结构计算,因为预测的结构可以与新的立体数据集成。场景流的其他应用包括各种动态渲染和解释任务,从慢动作回放的生成,到人类动作的理解和建模。
1.1 相关工作
计算场景的三维运动是计算机视觉中的一项基本任务,其方法多种多样。如果场景是刚性的,并且相机是标定的,那么三维的场景结构和相对运动能够用structure-from-motion从单目的视频序列中被计算出来[ullman 1979]。如果场景仅是分段刚性的,则可以用structure-from-motion的扩展,例如[Zhang and Faugeras, 1992a][Costeira and Kanade, 1998]
尽管非刚体的限制可以由structure-from-motion这种范式来进行分析,但是一般非刚体运动在没有对场景进行额外的假设时,无法实现单目相机的估计。然而,给定足够强的关于场景的先验假设,从单目视图中恢复三维非刚体运动是可能的。例如以可变形模型[Pentland and Horowitz, 1991] [ Metaxas and Terzopoulos , 1993]的形式或运动最小化对刚体运动[ Ullman , 1984]的偏差的假设。单目非刚体运动估计和计算所用的假设的调研见[Penna, 1994]
另一种常见的恢复三维运动的方法是使用多个相机,并将立体和运动结合在一个称为motion-stereo的方法中。几乎所有的motion-stereo算法都是假设场景是刚性的,例如可见[Waxman and Duncan, 1986], [Young and Chellappa, 1999],and[Zhang and Faugeras, 1992b]。一篇显式结合两个光流场的论文是[Shi et al., 1994]。在本文中,分析和实现都只适用于相机的某些简单运动(即平移)。
一些立体运动的论文考虑了非刚体运动,包括[Liao et al., 1997] and [Malassiotis and Strintzis, 1997]。前者使用基于松弛的算法在时间域和空间域协同匹配特征。因此它不提供稠密运动。后者在上述单目方法的推广中使用网格作为可变形模型。除了需要场景的先验模型外,大多数基于形变模型的运动立体方法对于我们的立体预测应用来说效率太低。
2. 图片构成的先验知识
如图1所示,考虑固定相机i拍摄的非刚体运动的表面f (x; y; z; t)=0,其3×4的投影矩阵为Pi。相机i拍摄的图像序列Ii=Ii( ui ,vi ; t )的形成有两个方面:( 1 )相机和表面的相对几何关系;( 2 )光照和表面光度。
2.1 相机和表面的相对几何关系
曲面上一点( x ,y ,z)与其在相机i中的图像坐标( ui ; vi )的关系为:
其中[ Pi ] j是Pi的第j行。式( 1 )和式( 2 )描述了从曲面上一点x = ( x ,y,z)到其在相机i中的图像ui = ( ui,vi )的映射。在没有表面知识的情况下,这些方程是不可逆的。给定f,它们可以被反演,但反演需要空间中的一条射线与曲面f相交。
图1:一个非刚体表面f (x, y, z; t)=0相对于固定世界坐标系( x ,y,z)运动,表面的法线为n=n (x, y, z; t)。假定表面为Lambertian,反射率为![]() ,光照通量(辐照度)为E。第i个相机在空间固定,对于一个坐标系( ui,vi )可以由3×4维的相机矩阵Pi表示,获得的图像序列由Ii=Ii( ui ,vi ; t )表示
,光照通量(辐照度)为E。第i个相机在空间固定,对于一个坐标系( ui,vi )可以由3×4维的相机矩阵Pi表示,获得的图像序列由Ii=Ii( ui ,vi ; t )表示
x和![]() 之间的微分关系可以用一个2×3的Jacobian矩阵
之间的微分关系可以用一个2×3的Jacobian矩阵![]() 表示。雅克比矩阵的3列存储了x,y,z中每单位变化的投影图像坐标的微分变化。通过对方程( 1 )和( 2 )进行符号微分,可以得到
表示。雅克比矩阵的3列存储了x,y,z中每单位变化的投影图像坐标的微分变化。通过对方程( 1 )和( 2 )进行符号微分,可以得到![]() 关于x的闭式表达式。雅可比矩阵
关于x的闭式表达式。雅可比矩阵![]() 描述了曲面上一点的微小变化之间的关系及其在相机i的图像通过
描述了曲面上一点的微小变化之间的关系及其在相机i的图像通过![]() 。类似地,逆雅可比
。类似地,逆雅可比![]() 描述了相机i图像中某点的微小变化与该点通过
描述了相机i图像中某点的微小变化与该点通过![]() 在场景中成像的关系。
在场景中成像的关系。
由于图像坐标并不唯一地映射到场景坐标,因此在不知道曲面的情况下无法计算逆雅克比。若已知曲面(及其梯度),则逆雅克比可以估计为以下两组线性方程组的解:
式( 3 )表达了![]() 的微小变化必然导致x的微小变化的约束,而x的微小变化在投影回图像时即为
的微小变化必然导致x的微小变化的约束,而x的微小变化在投影回图像时即为![]() 的原始变化。( 4 )式表达了由于世界上的对应点仍然位于曲面上,所以
的原始变化。( 4 )式表达了由于世界上的对应点仍然位于曲面上,所以![]() 的微小变化不会导致f的变化这一约束。
的微小变化不会导致f的变化这一约束。
式( 3 )和式( 4 )中的6个线性方程可以解耦为3个![]() 的方程和三个
的方程和三个![]() 的方程。对于
的方程。对于![]() 和
和![]() 都存在唯一解,当且仅当:
都存在唯一解,当且仅当:
由于![]() 与曲面法线n平行,因此方程组退化当且仅当加入投影相机中心和x的射线与曲面相切。
与曲面法线n平行,因此方程组退化当且仅当加入投影相机中心和x的射线与曲面相切。
2.2 光照和表面光度
在场景中的某一点x,t时刻在m方向上测量的辐照度或光照通量可以用E = E( m ; x ; t )表示[Horn, 1986]。这个6D辐照度函数E在[Adelson and Bergen, 1991]中被描述为plenoptic function。
我们用s = s( x,y,z ; t )表示t时刻地表( x,y,z)点的光的净定向辐照度。净方向辐照度s是一个矢量量,由辐照度E在可能方向的可见半球上的(矢量)表面积分给出:
其中![]() 为光线落在表面法线为n的曲面片上的方向半球。
为光线落在表面法线为n的曲面片上的方向半球。
假设表面为Lambertian且反照率![]() 。然后,假设点x = ( x,y,z)在第i个相机中可见,并且在图像Ii中显示的强度与该点的辐亮度成正比,即它是(即图像辐照度与场景辐亮度成正比[ Horn , 1986 ])的图像:
。然后,假设点x = ( x,y,z)在第i个相机中可见,并且在图像Ii中显示的强度与该点的辐亮度成正比,即它是(即图像辐照度与场景辐亮度成正比[ Horn , 1986 ])的图像:
其中C是一个常数,仅取决于透镜的直径和透镜与像面的距离。图像像素![]() 和表面点
和表面点![]() 由式( 1 )和( 2 )联系起来。
由式( 1 )和( 2 )联系起来。
3. 2D光流
设![]() 为曲面上某点的三维路径,该点在相机i中的图像为
为曲面上某点的三维路径,该点在相机i中的图像为![]() 。该点的三维运动为
。该点的三维运动为![]() ,其投影的二维像运动为
,其投影的二维像运动为![]() 。二维流场
。二维流场![]() 通常被称为光流。由于点
通常被称为光流。由于点![]() 在表面移动,自然假设其反照率
在表面移动,自然假设其反照率![]() 保持不变;即我们假设:
保持不变;即我们假设:
(对于一个可变形的移动表面,无论如何只有像反照率这样的表面特性才能区分点)。光流算法的基础就是方程:
其中![]() 是图像的空间梯度,
是图像的空间梯度,![]() 是光流,
是光流,![]() 是图像强度的瞬时变化率
是图像强度的瞬时变化率![]() 。
。
项![]() 取决于表面的形状(n)和照明( s )。为了避免对三维场景结构的明确依赖,通常假设
取决于表面的形状(n)和照明( s )。为了避免对三维场景结构的明确依赖,通常假设
是常数(![]() )。在均匀光照或表面法线不快速变化的情况下,该假设成立。
)。在均匀光照或表面法线不快速变化的情况下,该假设成立。
在这两种情况下,![]() 都趋于零,我们得到了"微分"光流算法[ Barron等, 1994]使用的Normal Flow或Gradient Constraint方程:
都趋于零,我们得到了"微分"光流算法[ Barron等, 1994]使用的Normal Flow或Gradient Constraint方程:
利用这一约束,大量的光流![]() 估计算法被提出。最近的一项调查见[ Barron, 1994]
估计算法被提出。最近的一项调查见[ Barron, 1994]
4. 3D场景流
与光流描述图像中的瞬时运动场一样,我们可以将场景流看作描述场景中每一点运动的三维流场![]() 。2.1节的分析只针对固定时间t。现在假设场景中有一个点
。2.1节的分析只针对固定时间t。现在假设场景中有一个点![]() 在运动。该点在相机i的图像为
在运动。该点在相机i的图像为![]() 。若相机不运动,则
。若相机不运动,则![]() 的变化率唯一确定为:
的变化率唯一确定为:
如果不知道曲面f的先验信息,反演这种关系同样是不可能的。为了反演,注意到x不仅依赖于![]() ,还依赖于时间,通过曲面
,还依赖于时间,通过曲面![]() 间接得到。即
间接得到。即![]() 。将该表达式对时间做微分可得
。将该表达式对时间做微分可得
这个方程说世界上一个点的运动是由两个分量组成的。首先是场景流在与曲面相切且经过x的平面上的投影。这是通过取图像平面(光流![]() )上的瞬时运动,利用逆雅克比
)上的瞬时运动,利用逆雅克比![]() 将其投影到场景中得到的。
将其投影到场景中得到的。
第二项是由固定像素成像的场景中点的三维运动对场景流的贡献。它是![]() 对应的x沿射线的瞬时运动。
对应的x沿射线的瞬时运动。 的大小是(正比于)表面f沿这条射线深度的变化率。
的大小是(正比于)表面f沿这条射线深度的变化率。 的推导见附录A。
的推导见附录A。
这里有三种计算场景流的主要方式,这取决于当时对场景的了解:
图2:显示场景运动的图像序列。由于篇幅所限,本文仅给出t = 1时的场景流结果。扩展序列的提出是为了帮助读者可视化三维运动。
1、完全已知场景的瞬时结构,包括表面法线、深度图以及这些深度图的时间变化率。
2、只知道立体的对应关系。由于我们工作在校准的环境中,这相当于拥有深度图。然而,它不包括深度图的表面法线和时间变化率。
3、完全未知的场景结构。我们甚至不知道通信信息。
每一种情况都导致了不同的场景流估计策略。似乎很直观的是,对场景结构的了解越少,就需要使用更多的光流,而这一结果确实来自于用于计算场景流的线性方程组的退化量。下面分别介绍三种情况下的算法。我们还使用从非刚性、动态变化的场景的多个图像序列(从不同角度捕捉)计算的流结果证明了它们的有效性。其中一个这样的图像序列如图2所示。
4.1 表面几何知识完备
如果曲面f是完全已知的(具有较高的准确性),则可以在每一点计算曲面梯度![]() 。通过求解式( 3 )和( 4 )中的6个线性方程组,可以估计出逆Jacobian
。通过求解式( 3 )和( 4 )中的6个线性方程组,可以估计出逆Jacobian ![]() 。给定雅克比逆,由光流
。给定雅克比逆,由光流![]() 利用式( 13 )估计场景流:
利用式( 13 )估计场景流:
完整的场景结构知识使我们能够从一个光流计算场景流,(以及该图像对应的深度图的变化率。)这两部分信息分别对应场景流的两个组成部分;将光流投影到经过x的切平面上,深度图的变化率被映射到沿光线经过场景点x和相机投影中心的一个分量上。
图3:图2中同一相机在t = 1时刻的水平和垂直光流。较暗的像素分别表示帧的左边和顶部的运动。
注意,在计算逆雅克比时,我们假设曲面是局部平面的。由于曲面是已知的,因此可以在图像中投影"流动"的点,并将此射线与曲面相交。我们目前不执行此操作来为每个像素保存一个expensive的射线-表面交点。
如果只使用一个光流,则只能计算场景中在该图像中可见的点的场景流。在多个相机中使用多个光流是可能的,以获得更好的能见度,并获得更大的鲁棒性。同时,只有当深度图的变化是有效的- -即当单个像素随着时间的变化看到表面的相邻部分时,才会恢复流。如果一个表面的运动相对于它的大小很大,那么一个像素会看到不同的表面,并且不能计算流量。
考虑如图2中序列所示的场景。由于篇幅限制,本文只给出时间t = 1时的场景流结果。场景流是由多个距离图像的体素合并得到的模型的深度图计算得到的,每个深度图像都使用立体计算,如[ Rander, 1996]所述。另一个输入是图3所示的光流,它使用分层版本的Lucas - Kanade光流算法计算。最终的输入是深度图的时间变化率,通过两个独立计算的体素模型之间的差异来估计。
图4:计算场景流程。模型上的原始点以灰色显示。这些点"流动"到的位置用黑色表示。这些流动点构成了模型在t = 2时刻的预测
图4展示了模型上可见点集的场景流计算结果。原始点以浅灰色显示。原始点通过添加场景流"流动到"的点以黑色显示。因此,较暗的点代表一个模型在时间t = 的2预测。它们可用于加快形状恢复的效率和提高鲁棒性。在图4中可以看出,球员在右侧(带球运动员)上的弯曲运动得到恢复,球的向下(并且有些偏侧)运动也得到恢复。左侧(面对球的球员)的玩家的主要运动是左臂的向上运动,部分恢复。对于手臂上的一些点,没有恢复出流,这是因为手臂相对于其尺寸而言移动得非常快。许多像素即使在一个时间步内也能看到完全不同的表面。因此,这些曲面上的点的深度信息的变化率是无效的,无法对这些点进行流量估计。
4.2已知图像对应关系
第二个主要情况是当场景的结构不完全已知,但是图像之间的对应关系是可用的。在我们的校准设置中,可以使用对应关系来计算深度图,但是这些深度图可能噪声太大,无法估计表面法线和时间变化率。这种情况屡见不鲜。例如,它在基于图像的建模和渲染问题中具有典型性。虽然这些问题通常只考虑静态场景,但场景流可以作为一种手段,将基于图像的建模方法扩展到时域的动态场景。
如果曲面不完全已知,则无法直接从一个相机求解![]() 。相反,考虑场景与光流之间的隐式线性关系,如式( 12 )中的雅克比所描述。
。相反,考虑场景与光流之间的隐式线性关系,如式( 12 )中的雅克比所描述。
这组方程对![]() 提供了两个线性约束。因此,如果我们有N > 2个摄像机,我们可以通过建立方程组
提供了两个线性约束。因此,如果我们有N > 2个摄像机,我们可以通过建立方程组![]() 来求解
来求解![]() 。其中:
。其中:
这给了我们3个未知数的2N个方程,因此对于![]() 我们有一个过约束系统并且可以找到场景流的一个估计。(当且仅当点x和N个相机中心共线时,该方程组退化.) B的奇异值分解给出了最小化通过将场景流重新投影到每个光流上得到的误差的最小平方和的解。
我们有一个过约束系统并且可以找到场景流的一个估计。(当且仅当点x和N个相机中心共线时,该方程组退化.) B的奇异值分解给出了最小化通过将场景流重新投影到每个光流上得到的误差的最小平方和的解。
我们实现了上述算法,并将其应用于上一节中使用的相同序列,但不使用深度图的表面法线或变化率。我们使用了来自15个不同相机的光流。这种大量光流的使用保证了我们想要计算场景流的每个点都至少被2或3个摄像机看到。
图5:针对模型上的点显示场景流的大小(其位置由4个相机的深度图投影到场景中得到)。场景流的大小显示为强度。可以看出,最大的运动发生在后排的球和人的手臂上,而最小的运动发生在队员的脚附近。
图5显示了计算场景流的大小。计算得到的x、y和z方向流的绝对值被平均并显示为每个点的强度。由于图像对应和相机标定为我们提供了深度图,因此场景流被计算为一组点,这些点的位置由4个相距较远的相机的深度图投影到场景中得到。可以看出,小球的运动和后排人的左臂垂直运动最为显著。
图6:初始点云显示为浅灰色,而这些点流动到的点集显示为黑色。可以看出,球员向下和向右都有明显的三维运动。
图7:流动点(黑色)与下一个时刻独立计算模型(浅灰色)的比较。可以看出,流动点在下一时刻对模型是一个很好的近似。
图6和图7展示了持球运动员的一个特写。在图6中,浅灰色的点表示t = 1时刻的模型,它们被估计的场景流所取代,以给出颜色较深的点。相同的流点如图7所示,除了在t = 2时的浅灰色点现在代表模型,使用立体和体积合并[ Rander, 1996]独立计算。从图中可以清楚地看到,使用场景流的点的位移导致它们几乎完全移动到"真实"模型上。因此,场景流可以作为后续时间间隔内场景结构的预测器。
4.3 没有表面的知识
如果点x位于曲面上,则对于每个相机i,式( 12 )必须成立。因此,可以将式( 12 )在相机间的一致程度作为基于流的重建算法的信息。然而,这种方法很容易受到异常值的影响。单个错误的大量级流动总会使方程不一致。因此,我们采取略有不同的做法。
方程( 12 )的解可以写成如下形式:
其中![]() 是
是![]() 的伪逆,
的伪逆,![]() 是穿过像素
是穿过像素![]() (见附录A)的射线方向,通时
(见附录A)的射线方向,通时![]() 是依赖于曲面f瞬时性质的未知常数。(式( 16 )成立,因为
是依赖于曲面f瞬时性质的未知常数。(式( 16 )成立,因为![]() 在
在![]() 的零空间中)。因此,我们对场景流有如下约束:
的零空间中)。因此,我们对场景流有如下约束:
其中![]() 是垂直于相机中心和光流在图像平面上定义的平面的向量。因此,如果x实际上是曲面上的一点,那么向量
是垂直于相机中心和光流在图像平面上定义的平面的向量。因此,如果x实际上是曲面上的一点,那么向量![]() 应该全部位于平面(垂直于场景的流
应该全部位于平面(垂直于场景的流![]() )中。我们通过计算3×3的矩阵来形成向量共面性的度量:
)中。我们通过计算3×3的矩阵来形成向量共面性的度量:
其中![]() 被
被![]() 归一化为一个单位向量。归一化使得算法不易受到不正确的大量级流的影响。
归一化为一个单位向量。归一化使得算法不易受到不正确的大量级流的影响。![]() 的最小特征值M是非共面性的度量.因此,我们用
的最小特征值M是非共面性的度量.因此,我们用![]() 作为x位于曲面上的可能性的度量。( N为相机数量。)
作为x位于曲面上的可能性的度量。( N为相机数量。)
我们将场景离散成三维的体素数组,就像[ Seit and Dyer , 1997]的体素着色算法一样。然后计算每个体素的![]() ,忽略可见性,如[Collins, 1996]。以这种方式忽略可见性不会显著影响性能,因为我们的共面性度量没有受到异常值的显著影响。(如果需要的话,该算法可以扩展为以类似[ Seitz and Dyer , 1997 ]的方式跟踪能见度。)
,忽略可见性,如[Collins, 1996]。以这种方式忽略可见性不会显著影响性能,因为我们的共面性度量没有受到异常值的显著影响。(如果需要的话,该算法可以扩展为以类似[ Seitz and Dyer , 1997 ]的方式跟踪能见度。)
我们将该算法的结果展示在图8中。我们使用了CMU虚拟现实dome[Narayanan, 1998]的所有51个摄像头的数据(一部分数据来自于呈现在图2中的单个相机)。
图8:共面性度量![]() 的体绘制。可以看出,大体场景结构得到了较好的恢复。然而,需要注意的是,该算法仅恢复场景运动的结构。因此,场景中的某些部分,如腿部,与其他部分一样没有被恢复。
的体绘制。可以看出,大体场景结构得到了较好的恢复。然而,需要注意的是,该算法仅恢复场景运动的结构。因此,场景中的某些部分,如腿部,与其他部分一样没有被恢复。
![]() 提供的信息可以与传统信息源相结合,进一步增强立体的鲁棒性。对于所有的51个相机,我们计算了从t = 1到t = 2的光流。然后计算每个体素的共面性度量
提供的信息可以与传统信息源相结合,进一步增强立体的鲁棒性。对于所有的51个相机,我们计算了从t = 1到t = 2的光流。然后计算每个体素的共面性度量![]() 并进行阈值化。图8包含了结果的体绘制。可以看出,场景的大体结构得到恢复。但需要注意的是,这种基于流的重建算法只能恢复场景实际运动的结构。这就是场景的某些部分,如人的腿,没有完全恢复的原因。
并进行阈值化。图8包含了结果的体绘制。可以看出,场景的大体结构得到恢复。但需要注意的是,这种基于流的重建算法只能恢复场景实际运动的结构。这就是场景的某些部分,如人的腿,没有完全恢复的原因。
4.4三维法向流约束
光流![]() 是一个二维向量场,通常分为法向流和切向流两部分。法向流为图像梯度
是一个二维向量场,通常分为法向流和切向流两部分。法向流为图像梯度![]() 方向的分量,切向流为垂直于法向流的分量。由式( 11 )可以直接估计正常流的大小为:
方向的分量,切向流为垂直于法向流的分量。由式( 11 )可以直接估计正常流的大小为:
估计切流是一个不适定问题。因此,需要某种形式的局部平滑来估计完整的光流[ Barron, 1994]。由于切向流的估计是大多数算法中的主要困难,自然会问是否可以使用来自多个相机的法向流来估计三维场景流,而不必使用某种形式的正则化。
法向流动约束方程( 11 )可以改写为:
这是对场景流![]() 的分量的标量线性约束。因此,乍看之下,从三个这样的约束中直接估计场景流似乎是可能的。不幸的是,对方程( 7 )关于x求导我们看到:
的分量的标量线性约束。因此,乍看之下,从三个这样的约束中直接估计场景流似乎是可能的。不幸的是,对方程( 7 )关于x求导我们看到:
由于该表达式与相机i无关,而只取决于场景(地表反照率、场景结构n和光照s)的属性,因此式( 20 )中![]() 的系数在理想情况下应该始终相同。因此,式( 20 )的任意拷贝数都是线性相关的。事实上,如果方程不是线性相关的,那么可以用这个事实来推断x不是曲面上的点。(见4.3节。)
的系数在理想情况下应该始终相同。因此,式( 20 )的任意拷贝数都是线性相关的。事实上,如果方程不是线性相关的,那么可以用这个事实来推断x不是曲面上的点。(见4.3节。)
这个结果意味着如果不对问题进行某种形式的正则化,就不可能对物体上的每个点独立地计算三维场景流。然而,我们希望强调的是,这个结果并不意味着不能直接从正常流中估计其他有用的量,例如在[ Negahdaripour和Horn , 1987]和其他"直接方法"中。
5. 结论
三维场景流是动态场景的一个基本属性。它可以作为一种预测机制来构建更加鲁棒的立体算法,并用于各种场景解释和渲染任务。我们提出了一个从光流计算场景流的框架,假设场景的各种瞬时属性已知。我们打算扩展我们的框架,以纳入在下一个时刻独立计算的结构知识。我们还计划研究其他不使用光流计算场景流的算法,并开发定量评估其准确性的方法。
附录A: 计算
 是像素
是像素![]() 所成像的场景中点的三维运动。假设从第i个相机测量得到的表面深度为
所成像的场景中点的三维运动。假设从第i个相机测量得到的表面深度为![]() 。那么,点x可以写成
。那么,点x可以写成![]() ,
,![]() ,和
,和![]() 的函数形式如下:3×4相机矩阵
的函数形式如下:3×4相机矩阵![]() 可写为:
可写为:
其中![]() 是一个3×3矩阵,
是一个3×3矩阵,![]() 是一个3×1向量.相机的投影中心为
是一个3×1向量.相机的投影中心为![]() ,光线经过像素
,光线经过像素![]() 的方向为
的方向为![]() ,相机z轴方向为
,相机z轴方向为![]() 。利用简单的几何学,我们得到了(见图9):
。利用简单的几何学,我们得到了(见图9):
图9:给定相机矩阵![]() 和到表面的距离
和到表面的距离![]() ,通过像素
,通过像素![]() 的光线方向和相机的z轴方向可以推导出点x的表达式。这个表达式可以符号微分得到
的光线方向和相机的z轴方向可以推导出点x的表达式。这个表达式可以符号微分得到 是x,
是x,![]() 和
和![]() 的函数:
的函数:
(必须注意正确选择![]() 的符号,使向量
的符号,使向量![]() 指向场景。)若相机
指向场景。)若相机![]() 固定,则有:
固定,则有:
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第1张图片](http://img.e-com-net.com/image/info8/175b27f7b65a4f598ce4f56cf82b77e5.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第2张图片](http://img.e-com-net.com/image/info8/b3934b63af55446da7d6d103e10170ae.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第3张图片](http://img.e-com-net.com/image/info8/e01f6f8d3c144e63b4711abc39b87b97.jpg)
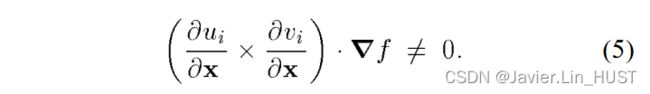
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第4张图片](http://img.e-com-net.com/image/info8/9d5ec8476a2040828bbb0c22cfaf4175.jpg)
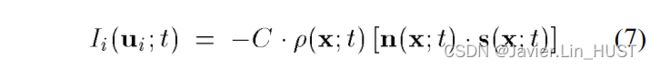
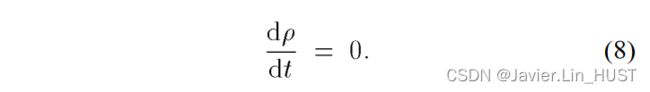
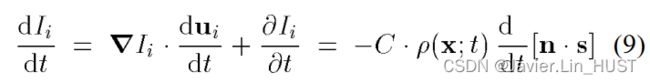
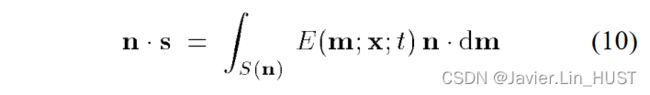

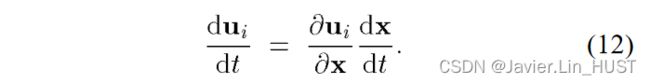
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第5张图片](http://img.e-com-net.com/image/info8/9829364999d9479e830fb7e8a90924c7.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第6张图片](http://img.e-com-net.com/image/info8/baabb14af6b24adbb472b968ee42bd40.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第7张图片](http://img.e-com-net.com/image/info8/db75f87f97564aaaa6e6f707dc856568.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第8张图片](http://img.e-com-net.com/image/info8/82aba83c9f524db3893d302b2edfcf7d.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第9张图片](http://img.e-com-net.com/image/info8/8e3db28fe9b349dab3b25c8bce9c5202.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第10张图片](http://img.e-com-net.com/image/info8/01c5fae79fdb47c3b8946cf7e5ff98d1.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第11张图片](http://img.e-com-net.com/image/info8/2b4ed8d2db6d4f218aa7e5c2ab9d1a7a.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第12张图片](http://img.e-com-net.com/image/info8/80be33e2de2a4cf5894c9e8a9516e955.jpg)
![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第13张图片](http://img.e-com-net.com/image/info8/7f325ee6830b4452bdb10592cc41cefd.jpg)

![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第14张图片](http://img.e-com-net.com/image/info8/d88e00acc857470c9a8c3ada481e838f.jpg)

![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第15张图片](http://img.e-com-net.com/image/info8/95a097c8d1fc462c9a4db9281ee3231c.jpg)


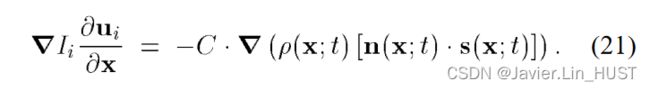
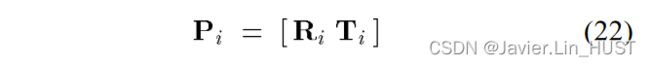

![[论文翻译]场景流估计的开山之作:Three-Dimensional Scene Flow(ICCV1999)_第16张图片](http://img.e-com-net.com/image/info8/328cab030dc74fb0a545fa9045cf018b.jpg)
