Python_Numpy库中各种矩阵基本运算(加、减、乘、点乘、点除、乘方、转置等)
Numpy中矩阵基本运算的实现。
目录
- 01-两个矩阵相加
- 02-矩阵与标量(常数)相加
- 03-两个矩阵相减
- 04-矩阵与标量(常数)的减法运算
- 05-求矩阵中每个元素的相反数
- 06-矩阵元素乘法(点乘)
-
- 06-1 两种方法实现矩阵元素乘法(点乘)
- 06-2-浮点数和unit8型矩阵做点乘的结果是什么数据类型的矩阵？
- 07-矩阵乘法运算
- 08-矩阵元素乘方运算
- 09-矩阵的元素除法(点除)[也叫真除-结果既有整数部分也有小数部分]
- 10-矩阵的元素除法(点除)取余
- 11-矩阵的元素除法(点除)取整
- 12-矩阵的转置
- 13-各种取整
-
- 13-1 四舍五入取整
- 13-2 向下取整
- 13-3 向上取整
01-两个矩阵相加
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
B = np.array([[2, 3, 4],
[5, 6, 7],
[8, 9, 10]], dtype='int8')
C = A+B
运行结果如下：
02-矩阵与标量(常数)相加
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
b = 3
C = A+b
运行结果如下：
03-两个矩阵相减
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
B = np.array([[2, 3, 4],
[5, 6, 7],
[8, 9, 10]], dtype='int8')
C = B-A
运行结果如下：
04-矩阵与标量(常数)的减法运算
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
b = 3
C = b-A
D = A-b
运行结果如下：
05-求矩阵中每个元素的相反数
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
B = -A
运行结果如下：
06-矩阵元素乘法(点乘)
06-1 两种方法实现矩阵元素乘法(点乘)
实现元素乘法有两种方法，一是用乘号，二是用函数multiply()。
下面的示例代码体现了这两种方法：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]], dtype='int8')
B = np.array([[2, 3, 4],
[5, 6, 7],
[8, 9, 10]], dtype='int8')
C = A*B # 用乘号实现矩阵元素乘法
D = np.multiply(A, B) # 用函数multiply()实现矩阵元素乘法
运行结果：
06-2-浮点数和unit8型矩阵做点乘的结果是什么数据类型的矩阵？
这里我们来探究一下，假如一个浮点数和unit8型矩阵做点乘会发生什么呢？
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='uint8')
b = 0.7
C = np.multiply(A, b)
运行结果如下：
可以Numpy在运算时是以保证精度为优先的，所以矩阵C的数据类型被转换为了float64型。
07-矩阵乘法运算
矩阵乘法运算也有两种方式实现，示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = np.array([[7, 8],
[9, 10],
[11, 12]], dtype='int16')
C = np.matmul(A, B) # 第一种方法实现矩阵乘法
D = np.dot(A, B) # 第二种方法实现矩阵乘法[利用向量的点积(也称为数量积)实现]
运行结果如下：
要注意：方法二实际上是利用向量的点积(点乘/数量积)实现的，当然，它有局限性，它只适用于向量或二维矩阵。
08-矩阵元素乘方运算
以矩阵A中的元素为底数，矩阵B中的元素为指数，
示例代码如下：
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = np.array([[6, 5, 4],
[3, 2, 1]], dtype='int16')
C = A**B
运行结果如下：
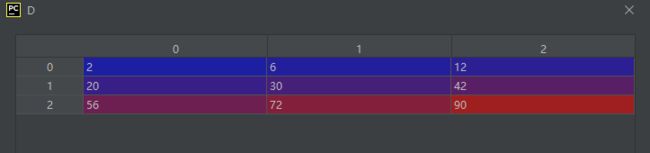
09-矩阵的元素除法(点除)[也叫真除-结果既有整数部分也有小数部分]
有三种方法实现元素除法(点除)，示例代码如下
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = np.array([[2, 6, 12],
[20, 30, 43]], dtype='int16')
C = B/A # 第一种方法实现元素除法(点除)
D = np.true_divide(B, A) # 第二种方法实现元素除法(点除)
F = np.divide(B, A) # 第三种方法实现元素除法(点除)
运行结果如下：
10-矩阵的元素除法(点除)取余
有三种方法实现元素除法(点除)取余，示例代码如下
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = np.array([[6, 6, 6],
[6, 6, 6]], dtype='int16')
C = B % A # 第一种方法实现元素除法(点除)取余
D = np.remainder(B, A) # 第二种方法实现元素除法(点除)取余
E = np.mod(B, A) # 第三种方法实现元素除法(点除)取余
运行结果如下：
11-矩阵的元素除法(点除)取整
有两种方法实现元素除法(点除)取整，示例代码如下
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = np.array([[11, 11, 11],
[11, 11, 11]], dtype='int16')
C = np.floor_divide(B, A) # 第一种方法实现元素除法(点除)取整
D = B//A # 第一种方法实现元素除法(点除)取整
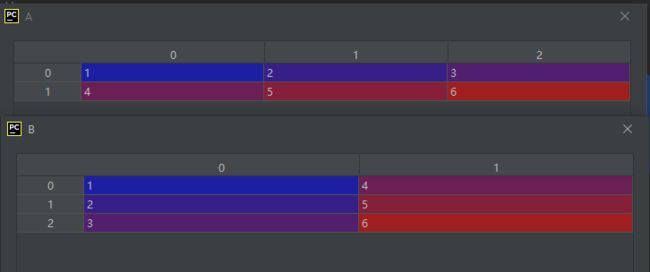
12-矩阵的转置
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]], dtype='int16')
B = A.T
运行结果如下：
13-各种取整
13-1 四舍五入取整
可以用方法around()实现四舍五入取整
around(a, decimals=0, out=None)
参数decimals 为要保留的小数位数， 默认值为0。 如果为-1，将在个位上进行四舍五入，如果为-2，将在十位上进行四舍五入。示例代码及运行结果如下：
import numpy as np
n = np.array([-0.746, 4.6, 9.4, 7.447, 10.455, 11.555])
around1 = np.around(n)
print(around1) # [ -1. 5. 9. 7. 10. 12.]
around2 = np.around(n, decimals=1)
print(around2) # [ -0.7 4.6 9.4 7.4 10.5 11.6]
around3 = np.around(n, decimals=-1)
print(around3) # [ -0. 0. 10. 10. 10. 10.]
13-2 向下取整
可以用方法floor()实现向下取整
示例代码及运行结果如下：
import numpy as np
n = np.array([-1.7, -2.5, -0.2, 0.6, 1.2, 2.7, 11])
floor = np.floor(n)
print(floor) # [ -2. -3. -1. 0. 1. 2. 11.]
13-3 向上取整
可以用方法ceil()实现向上取整
示例代码及运行结果如下：
import numpy as np
n = np.array([-1.7, -2.5, -0.2, 0.6, 1.2, 2.7, 11])
ceil = np.ceil(n)
print(ceil) # [ -1. -2. -0. 1. 2. 3. 11.]
延伸阅读：
归纳总结MATLAB中与矩阵运算有关的算术运算符(加、减、乘、除、点乘、点除、乘方、转置等)
OpenCV中的MAT类矩阵的各种基本运算及示例代码(加、减、乘、点乘、点除、乘方、累加、转置等)