机器学习（二）读取csv数据进行分析2

0_引言

笔者的环境为：windows10，python3.8，pycharm 2021.3

测试用例csv数据下载链接：链接

数据集如图：

1_统计分析

首先我们调用第三方库：pandas提取csv中的数据

import pandas as pd

data = pd.read_csv('StudentPerformance.csv')

基础分析

随后选取其中一列，选取以下方法对数据进行基本的统计分析

d1 = data['raisedhands']
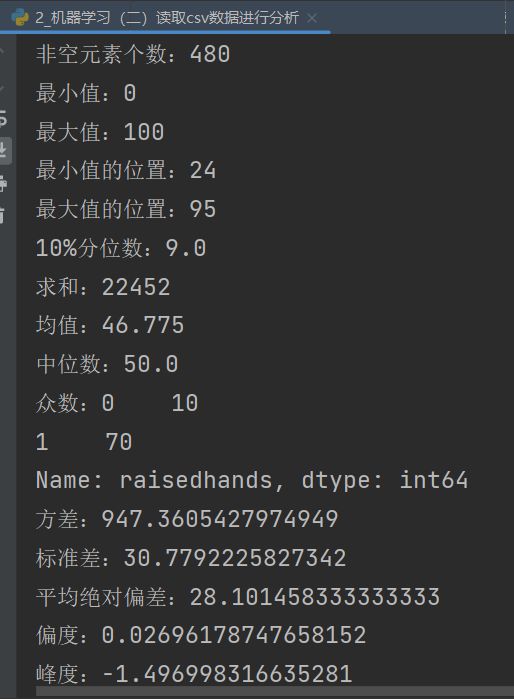
print('非空元素个数：' + str(d1.count()))  # 非空元素计算
print('最小值：' + str(d1.min()))  # 最小值
print('最大值：' + str(d1.max()))  # 最大值
print('最小值的位置：' + str(d1.idxmin()))  # 最小值的位置，类似于R中的which.min函数
print('最大值的位置：' + str(d1.idxmax()))  # 最大值的位置，类似于R中的which.max函数
print('10%分位数：' + str(d1.quantile(0.1)))  # 10%分位数
print('求和：' + str(d1.sum()))  # 求和
print('均值：' + str(d1.mean()))  # 均值
print('中位数：' + str(d1.median()))  # 中位数
print('众数：' + str(d1.mode()))  # 众数
print('方差：' + str(d1.var()))  # 方差
print('标准差：' + str(d1.std()))  # 标准差
print('平均绝对偏差：' + str(d1.mad()))  # 平均绝对偏差
print('偏度：' + str(d1.skew()))  # 偏度
print('峰度：' + str(d1.kurt()))  # 峰度
print('数据集整体描述：\n' + str(d1.describe()))  # 一次性输出多个描述性统计指标

相关系数

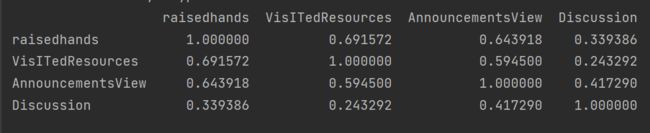
print(data.corr())

协方差矩阵

print(data.cov())

其他操作

删除列

data.drop('Discussion', axis=1)    # 删除Discussion列，axis=1必不可少

列排序

# 根据Discussion、raisedhands升序排序
data.sort_values(by=['Discussion','raisedhands'])  
# 根据Discussion、raisedhands降序排序
data.sort_values(by=['Discussion','raisedhands'], ascending=False)     

2_结构分析

首先import必要的库，设置绘图字体，导入数据

import matplotlib
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns

sns.set(font="Kaiti", style="ticks", font_scale=1.4)
matplotlib.rcParams['axes.unicode_minus'] = False
data = pd.read_csv('data4.csv')

第一步：数据集是否均衡

# 查看样本分布是否均衡
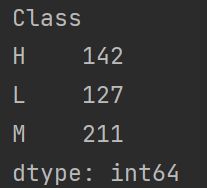
print(data.groupby(['Class']).size())

可以看出样本还是不太均衡的，M类居多

第二步：单属性异常值分析

连续值的异常值

"""
对于连续值来说，对于那些过大的数据值或太小的数据值对整体都会有很大的影响，不能很好地表现真实情况。
例如在反映公司的人均收入时，少部分人的年薪可能达到1000w甚至更高，而大部分公司职员的收入都在中等水平，
而这些较大值在统计公司人均收入水平时就会起到一个很大的拔高作用，使得失去了意义。
对于连续异常值的判断标准是我们通常会设置一个上界和下界，在上下界之外的都属于异常值，
而这个上下界的设定如下：设q_low和q_high分别为数据的下四分位数和上四分位数，value_low和value_high分别为下界和上界，
那么value_low=q_low-k*(q_high-q_low)，value_high=q_high+k*(q_high-q_low)，k通常取值1.5或3。
对于连续异常值的处理可以直接去掉（异常值不多的情况），也可以用边界值代替异常值。空值也可以作为异常值进行处理，对于连续值属性可以用均值来代替空值。
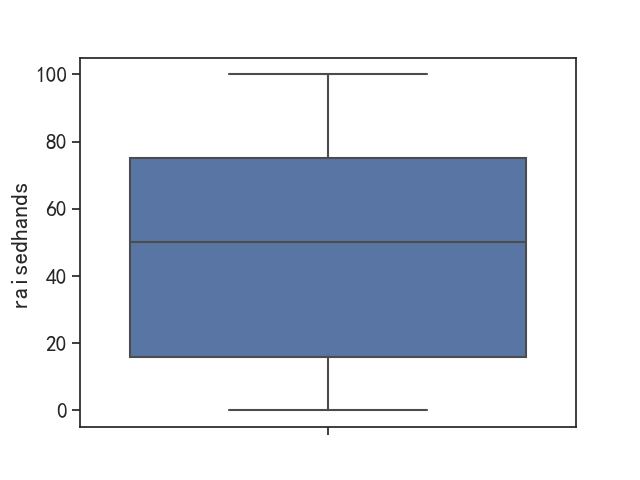
现在对上面的power特征进行异常值分析，这里加入可视化展示，通过可视化可以让数据更加直观，这里用到的是seaborn中的箱线图。
"""

plt.figure()
sns.boxplot(y=data["raisedhands"])
plt.show()

q_low = data["raisedhands"].quantile(q=0.25)
q_high = data["raisedhands"].quantile(q=0.75)
q_interval = q_high - q_low
index_high = data["raisedhands"] <= (q_high + 1.5 * q_interval)
index_low = data["raisedhands"] >= (q_low - 1.5 * q_interval)

plt.figure()
sns.boxplot(y=data["raisedhands"][index_low & index_high])
plt.show()

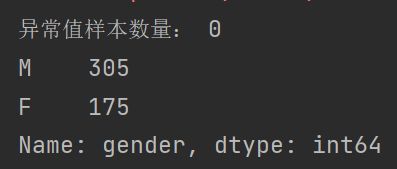
print("异常值样本数量：", len(data) - len(data[index_low & index_high]))
# 输出为0

可以看出，该特征不存在异常值

离散值的异常值

"""
离散异常值主要为那些在我们特征属性定义之外的值，例如空值，或者我们定义了工资水平为高中低三种值但却出现了其他值，这些都是异常值。
对于异常值在数量不大的时候我们都可以直接删除掉，对于空值和异常值可以使用众数来代替也可以把控制当做一个单独的值进行处理。

现在我们对 gender 进行分析：我们通过value_counts查看离散属性每个值的数量，我们发现除了 M 和 F 之外我们发现没有其它值出现，所以不存在异常值，如果建模阶段采用树模型是可以就算有空值也可以不对空值处理

"""

print(data['gender'].value_counts())

第三步：分布分析

"""
1.如何判断是不是正态分布？
对于获得的数据我们可以直接获得其概率分布，但是这样的得到的分布往往意义不大，所以我们通产常会判断它是否服从正态分布。通常我们会通过数据的偏度和峰度来判断是否是正态分布，偏度系数是数据平均值偏离状态的一种衡量，对于对称性分布而言平均值和中位数是比较接近的（例如正态分布），而非对称分布中位数和均值相差较大，这种分布也叫做有偏态的分布。
（1）偏度系数大于0，正偏（右偏），均值较大（相对于中位数而言）
（2）偏度系数小于0，负偏（左偏），均值较小
正态分布的峰度系数为3，如果某个分布的峰度系数与正态分布的峰度系数相差超过2，那么这个分布就不是正态分布。
"""

# 首先我们找出数据中的连续型变量：
# raisedhands,VisITedResources,AnnouncementsView,Discussion
labels = ['raisedhands', 'VisITedResources', 'AnnouncementsView', 'Discussion']

# 设置画布大小像素点
plt.figure(figsize=(14, 14), dpi=100)

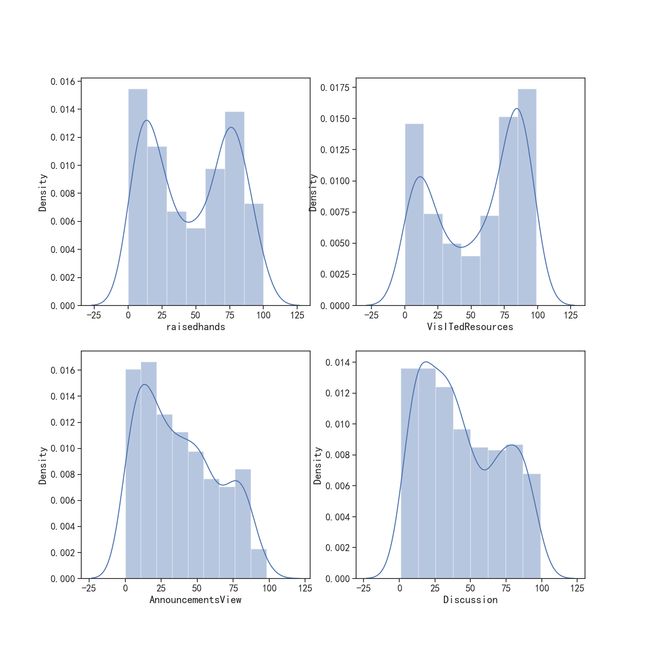
# 通过for循环将图像展示出来，可以看到这些数据并不是正态分布
for te, i in enumerate(labels):
    plt.subplot(2, 2, te + 1)
    print("-" * 25 + i + "-" * 25)
    print("偏度系数：", data[i].skew())
    print("峰度系数：", data[i].kurtosis())
    sns.distplot(data[i])
plt.show()

# 离散型变量结构分析
"""
研究一个总体的组成结构方面的差异和相关性。
（1）静态结构分析：直接分析总体的组成。例如直接分析第一产业、第二产业、第三产业的比例为13%，46%，41%，
    这样就确定了我国的产业结构，同时和美国、日本等进行比较，来衡量我们三大产业是否均衡，下一步如何决策等。
（2）动态结构分析：以时间为轴分析结构变化的趋势。例如知道十五期间三大产业的占比，
    那么对于十一五期间三大产业的结构是如何变化的就能够反映国家性质上的反应方向。
"""

# 找出数据中的离散型变量
labels1 = ['gender', 'NationalITy', 'PlaceofBirth', 'StageID', 'GradeID', 'SectionID', 'Topic', 'Semester', 'Relation', 'ParentAnsweringSurvey', 'ParentschoolSatisfaction', 'StudentAbsenceDays', 'Class']
# 设置画布尺寸
plt.figure(figsize=(32, 32))
for te, i in enumerate(labels1):
    plt.subplot(4, 4, te + 1)
    print("-" * 25 + i + "-" * 25)
    sns.countplot(x=i, data=data)
    print(data[i].value_counts())
plt.show()

3_交叉验证

最后我们对模型进行基于随机森林的交叉验证，找出最优方案

# 首先导包
from sklearn.datasets import load_wine
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
# 导入交叉验证模型
from sklearn.model_selection import cross_val_score, StratifiedKFold

# 载入数据
data = pd.read_csv('StudentPerformance.csv')
# 由于数据集中有很多离散型变量，这些变量的值为字符串，不利于建模，因此，需要先对这些变量进行重新编码。
# 离散型变量的重编码
for feature in data.columns:
    if data[feature].dtype == 'object':
        data[feature] = pd.Categorical(data[feature]).codes

X = data.drop('Class', axis=1).values.tolist()
y = data['Class'].values.tolist()

# 将模型设置为随机森林
model = RandomForestClassifier()

print('start to run')
# 使用交叉验证法对SVC进行评分
score = cross_val_score(model, X, y)

print('交叉验证得分：{}'.format(score))
# 获取平均分数
print('交叉验证平均得分：{:.3f}'.format(score.mean()))

print('\n====================== 设置cv=10 ')
# 数据集拆分成10个部分来评分，cv=10
scores = cross_val_score(model, X, y, cv=10)
print('交叉验证得分：{}'.format(scores))
# 获取平均分数
print('交叉验证平均得分：{:.3f}'.format(scores.mean()))

# # 打印数据集的分类标签
# print('分类标签：\n{}'.format(y))

print('\n====================== 使用StratifiedKFold 分层交叉验证')
strKFold = StratifiedKFold(n_splits=10, shuffle=True, random_state=0)
scores = cross_val_score(model, X, y, cv=strKFold)
print("straitified cross validation scores:{}".format(scores))
print("Mean score of straitified cross validation:{:.3f}".format(scores.mean()))

print('\n====================== 使用KFold 交叉验证')
strKFold = KFold(n_splits=10, shuffle=True, random_state=0)
scores = cross_val_score(model, X, y, cv=strKFold)
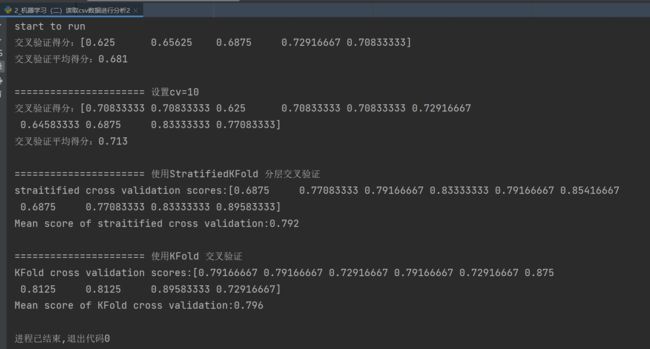
print("KFold cross validation scores:{}".format(scores))
print("Mean score of KFold cross validation:{:.3f}".format(scores.mean()))

可以看到，几种交叉验证的评分都不是很高，不过不慌张，在下一篇我们将开始进入机器学习模型构建阶段，将采用各种方式进行优化，达到令人满意的效果