Contrastive Clustering论文笔记
Contrastive Clustering
- 论文链接
- 总结
- 对比训练
- 网络
-
- 1. PCB
- 2. ICH
- 3. CCH
论文链接
总结
CC:将得到的特征向量分别放入到实例层和聚类层中同时进行优化。
对比训练
对比训练的思想就是将原始数据映射到一个新的向量空间,在这个向量空间中,正样本对之间的相似性和负样本之间差异被最大化。
网络

网络分为三个部分:a pair construction backbone (PCB), an instance-level contrastive head (ICH),and a cluster-level contrastive head (CCH)。
1. PCB
选定一个转换方法集合 T T T(文中选择的是ResizedCrop,ColorJitter, Grayscale, HorizontalFlip, and GaussianBlur),对输入的图片x,从 T T T中随机抽取两种转换方法 T a 、 T b T^a、T^b Ta、Tb,分别对x进行转换,得到增广后的图片 x a 、 x b x^a、x^b xa、xb。接着构造一个神经网络(常规的卷积网络如resnet等),分别以 x a 、 x b x^a、x^b xa、xb作为输入,得到它们的特征向量(1*F的向量)。按照这个方法对所有输入的图片进行处理,将使用 T a T^a Ta方法进行增广的图片对应的特征向量拼接在一起,就得到了特征矩阵 h a h^a ha,同理可以得到 h b h^b hb。
2. ICH
首先,要定义对比训练中的正负样本对是什么。评价的标准可以不同,在论文中是让由同一个图像x增广出的图像 x a 、 x b x^a、x^b xa、xb为正样本对,而与除此之外的所有图像互为负样本对。
然后,在得到上述的特征矩阵 h a 、 h b h^a、h^b ha、hb后,论文中并没有直接对它们进行操作,而是让它们先经过非线性的MLP(激活函数为ReLU),将他们映射到子空间,得到 z a 、 z b z^a、z^b za、zb后,再进行之后的操作。CCH部分也需要进行这样的操作,只不过CCH部分最后连接了一层sigmoid函数。据作者说经过这样一层映射后可以减少之后对比训练时的信息损失。
在ICH中, z i k ( i ∈ [ 0 , N ) , k ∈ { a , b } ) z^k_i(i\in[0,N),k\in\{a,b\}) zik(i∈[0,N),k∈{a,b})的下标 i i i代表着 z z z的第 i i i行,即第 i i i张图片;上标 k k k代表着第 k k k种转换。可以认为, z i k z^k_i zik就是经过第k种转换后第i张图的特征向量,两张图之间的相似性可以用如下公式进行比较:
即向量之间夹角的cos值。
对于一个 z i k z^k_i zik,它的损失如下:
其中,分母是经过变换a中第i个照片与变换a种所有照片的相似度之和,加上变换a中第i个照片与变换b中所有照片的相似度之和。分子是变换a、b中第i个照片的相似度。 τ \tau τ是温度参数,它越大,得到的结果越平滑,同时,loss也就越大;所以,它可以用来在前期逃脱局部最小值,但是,需要随着迭代轮数增多将其减小防止后期梯度过大。
可以看出,这个loss的目的就是最大化由同一张图片x,增广出的图片 x a 、 x b x^a、x^b xa、xb的相似度。
这一部分最终的损失如下:
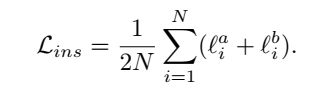
3. CCH
CCH部分整体和ICH部分相同,只不过最终得到的 y a 、 y b y^a、y^b ya、yb是N*M的矩阵,其中N为输入图像数目,M为簇的个数。
在CCH中, y i k ( i ∈ [ 0 , M ) , k ∈ { a , b } ) y_i^k(i\in[0,M),k\in\{a,b\}) yik(i∈[0,M),k∈{a,b})是 y k y^k yk矩阵的第i列,代表经过第k种变换后第i簇的特征向量(对于 y k y^k yk中的点 y i j k y_{ij}^k yijk而言,代表了 y k y^k yk中第i个图属于第j簇的概率,所以 y i k y_i^k yik可以表示该簇的特征向量)。
两张图的相似性标准和损失函数基本和ICH相同:


值得一提的是,在这一部分损失函数中,引入了 H ( Y ) H(Y) H(Y),它的表达式为:
![]()
其中, P ( y i k ) = ∑ j = 1 N Y j i k / ∣ ∣ Y ∣ ∣ 1 P(y_i^k) = \sum_{j=1}^N Y^k_{ji}\ /\ ||Y||_1 P(yik)=∑j=1NYjik / ∣∣Y∣∣1, ∑ j = 1 N Y j i k \sum_{j=1}^NY^k_{ji} ∑j=1NYjik即对第i簇的特征向量各个位置进行累加求和, ∣ ∣ Y ∣ ∣ 1 ||Y||_1 ∣∣Y∣∣1是矩阵的第一范式,即对矩阵Y的所有列向量分别求和,然后选出它的最大值(也可以称为对各簇的特征向量进行累加和),数学表达式为 m a x ∑ j = 1 N Y j i k ( i = 0 , 1 , 2.... M − 1 ) max\sum_{j=1}^NY^k_{ji}(i=0,1,2....M-1) max∑j=1NYjik(i=0,1,2....M−1);
这里的 P ( y i k ) P(y_i^k) P(yik)可以理解簇的概率分布。而通过对H(Y)表达式的分析,可以很容易地分析出当图像分布于各簇的概率相同时,H(Y)可以取得最大值。而这正是引入这个部分的意义:防止所有的图像都被分到一个簇里面。
BS3_1 11th