递归神经网络之父讲述现代人工智能简史

现代人工智能的历史，主要由人工神经网络（NN）和深度学习主导。本文来自递归神经网络之父Jürgen Schmidhuber的AI播客。文章从2022年的视角出发，提供了一个重要的时间线，将人工神经网络、深度学习、人工智能、计算机科学和一般数学历史上最重要的相关事件逐一盘点。它还驳斥了某些流行但具有误导性的深度学习的历史描述，并补充了 Schmidhuber之前的深度学习调查，提供了数百个额外的参考资料。最后在一个更广泛的时空背景下进行了总结。本篇文章也是 Schmidhuber即将出版的人工智能书籍中的一章。智源社区进行了完整编译。

jürgen schmidhuber

递归神经网络之父

Jürgen Schmidhuber出生于德国，是瑞士人工智能实验室（IDSIA）的研发主任，被称为递归神经网络之父。Schmidhuber本人创立的公司Nnaisense正专注于人工智能技术研发。1997年，和Sepp Hochreiter等一道发表了著名论文Long Short Term Memory（LSTM）。

简介

历史的发展总是伴随着不断的修正。比如138亿年前的大爆炸，现在被广泛认为是万物历史中一个重要的节点。然而，就在几十年前，人类还完全不了解它，他们对宇宙的起源一直抱有一种错误的想观点，人工智能（AI）的发展史也是如此。

一部写于20世纪80年代的人工智能史，会强调诸如定理证明、逻辑编程、专家系统和启发式搜索等主题。1956年在达特茅斯举行的会议上，John McCarthy创造了"AI "一词；实用人工智能至少可以追溯到1914年，Leonardo Torres y Quevedo制造了第一个可行的的国际象棋“终结者”；至于人工智能理论，至少可以追溯到1931-1934年，库尔特-哥德尔（Kurt Gödel）确定了基于计算的人工智能的基本局限性。

一部写于21世纪初的人工智能史，则会更加强调诸如支持向量机和核方法、贝叶斯(实际上是拉普拉斯或桑德森)推理以及其他概率论和统计的概念、决策树、 集成方法、群体智能和进化计算等，这些技术当时推动了许多成功的人工智能应用。

而在2020年写人工智能史，必须强调一些复古的概念，比如链式规则和通过梯度下降训练的深度非线性人工神经网络（NN），特别是基于反馈的递归网络。

过去的一些NN研究受到了人脑的启发。人脑有大约1000亿个神经元，每个神经元平均与10000个其他神经元相连。其中一些是输入神经元，为其他神经元提供各种数据（声音、视觉、触觉、疼痛、饥饿）；另一些是控制肌肉的输出神经元。而隐藏在两者之间的大多数神经元，则是思考发生的地方。大脑通过改变连接的强度或权重来学习的，这决定了神经元相互影响的强度，并且编码了个人所有的经验。NN也是如此，因此，它能更好地学习识别语音、笔迹或视频，或者驾驶汽车等等。

1676: 逆向信用分配的链式规则

1676年，戈特弗里德-威廉-莱布尼茨在一本回忆录中发表了微分的链式规则；纪尧姆-德-霍皮塔尔在他1696年关于莱布尼茨微分的教科书中描述了这个规则。最流行的NN拥有神经元（节点），它们计算来自其他神经元输入的可微分函数，而这些输入神经元同样也计算来自其他神经元的输入的可微分函数……如果稍微修改一下早期函数的参数或权重，最终函数的输出将如何变化？这里，链规就是计算答案的基本工具。

Augustin-Louis Cauchy在1847年首次提出了梯度下降（GD）技术（后来Jacques Hadamard详细提出；随机梯度下降（SGD）则是由Herbert Robbins和Sutton Monro 1951年提出的）。为了教一个NN将训练集的输入模式转化为所需的输出模式，所有NN的权重都要在最大的局部改进方向上迭代，以创造一个稍好的NN，如此反复，直到找到一个满意的解决方案。

~1800: 第一个神经网络、

线性回归与浅层学习

1805年，Adrien-Marie Legendre发表了线性神经网络（NN）。约翰-卡尔-弗里德里希-高斯（Johann Carl Friedrich Gauss）也被认为在1795年左右完成了未发表的相关工作。

这个2个多世纪前的NN有两层：包括几个输入单元的输入层，和一个输出层。每个输入单元可以容纳一个实值的数字，并通过一个具有实值权重的连接与输出相连。NN的输出是输入和其权重的乘积之和。给出一个输入向量的训练集和每个向量的期望目标值，调整NN的权重，使NN输出和相应目标之间的平方误差之和最小。

1795年，高斯使用了线性神经网，但Legendre在1805年首先发表了这个方法。那时它被称为最小二乘法，或广泛称为线性回归。它的原理在数学上与今天的线性NN相同。这种简单的NN执行 "浅层学习"。今天，许多NN课程都从介绍这种方法开始，然后转向更复杂、更深入的NN。

1920-1925:

第一个递归网络结构（RNN）

1924年，恩斯特-伊辛发表了第一个递归网络架构：伊辛模型（或伦茨-伊辛模型）。与更为有限的前馈网络（FNN）不同，递归网络（RNN）有反馈连接，这样，信号可以沿着定向连接从某些内部节点到其他节点，最终在开始的地方结束。这对于在序列处理过程中实现对过去事件的记忆至关重要。

第一个非学习型RNN架构（Ising模型或Lenz-Ising模型）由物理学家Ernst Ising和Wilhelm Lenz在20世纪20年代提出并分析。它对输入条件的反应进入平衡状态，是学习型RNN的基础。

~1972: 第一个发表的学习型人工RNN

1972年，甘利俊一（Shun-Ichi Amari）提出了Ising递归网的适应性。这是第一个发表的学习型人工递归神经网络。Shun-Ichi Amari使Lenz-Ising递归结构具有自适应性，这样它就可以通过改变其连接权重来学习将输入模式与输出模式联系起来。

10年后，Amari网络被重新发表。有人称它为霍普菲尔德网络或阿马里-霍普菲尔德网络。它不处理序列，而是对静态输入模式做出反应，进入一个平衡状态。Amari在1972年也发表了其序列处理的一般化。

早在1948年，阿兰-图灵就写出了与RNN有关的想法，但直到几十年后才首次发表，这解释了他的想法在当时的晦涩性。今天，最流行的RNN是下文提到的长短时记忆（LSTM），它已经成为20世纪被引用最多的NN。

1958: 多层前馈式NN（非深度学习）

Frank Rosenblatt不仅结合了线性NN和阈值函数，他还拥有更有趣、更深入的多层感知器（MLPs）。他的MLPs有一个带有随机权重的非学习第一层和一个适应性输出层。虽然由于只有最后一层会学习，这还不是深度学习，但Rosenblatt基本上给出了极端学习机（ELMs）的原理。今天，最流行的FNN是基于LSTM的Highway Net的一个版本，叫做ResNet，它已经成为21世纪被引用最多的NN。

1965: 第一次深度学习

1965年，乌克兰（苏联）的Alexey Ivakhnenko和Valentin Lapa为具有任意多隐藏层的深度MLP引入了第一个有效的深度学习算法。1971年的一篇论文描述了一个有8层的深度学习网，用他们被高度引用的方法进行训练，这种方法千禧年后仍然很流行，特别是在东欧，很多机器学习就诞生于此。

1967-68: 

通过随机梯度下降进行深度学习

Shun-Ichi Amari建议通过随机梯度下降（SGD），即Robbins & Monro在1951年提出的方法，以非递增的端到端方式从头开始训练多层的MLPs。Amari与他的学生Saito一起，在一个有两个可修改层的五层MLP中学习内部表征，该层被训练来分类非线性可分离的模式类。

1970: 反向传播算法

1960年，Henry J. Kelley在控制理论领域展示了反向传播的前身。与Linnainmaa的方法不同，20世纪60年代的系统通过标准的雅各布矩阵计算，将导数信息从一个 "阶段 "反向传播到前一个阶段，既没有解决跨阶段问题，也没有解决由于网络稀疏性带来的潜在额外效率提升。

1970年，Seppo Linnainmaa第一个发表了反向传播算法，这是在可微分节点网络中进行信用分配的著名算法，也被称为 "自动微分的反向模式"。它是广泛使用的NN软件包的基础，比如PyTorch和谷歌的Tensorflow。

反向传播本质上是为深度网络实现Leibniz链式规则的一种有效方式。1982年，Paul Werbos提出用该方法来训练NN。到1985年，David E. Rumelhart等人对已知方法的实验证明，反向传播可以在NN的隐藏层中产生有用的内部表征。至少对于监督学习来说，反向传播通常比Amari通过更一般的SGD方法（1967）进行的上述深度学习更有效率。

在2010年之前，许多人认为训练多层的NN需要无监督的预训练。2010年， Schmidhuber的团队和罗马尼亚博士后Dan Ciresan表明，深度FNNs可以通过普通反向传播来训练，且在重要的应用中根本不需要无监督的预训练。

1979: 

第一个深度卷积神经网络（CNN）

1979年，Kunihiko Fukushima介绍了具有交替卷积层和下采样层的基本卷积神经网络（CNN）。CNN是一种特殊前馈神经网络，在2010年彻底改变了计算机视觉领域。福岛还为NN引入了整流线性单元（ReLU）（1969年）。它们现在被广泛用于CNN和其他NN。

1987年，Alex Waibel将带有卷积的NNs与权重共享和反向传播相结合，并应用于语音。

1990年，Yamaguchi等人为TDNNs引入了一种流行的下采样变体，称为最大池，1993年，Juan Weng等人为高维CNNs引入了这种变体。

自1989年以来，Yann LeCun的团队对CNN的改进做出了贡献，特别是在图像方面。Baldi和Chauvin（1993年）首次将带有反向传播的CNN应用于生物医学/生物测量图像。

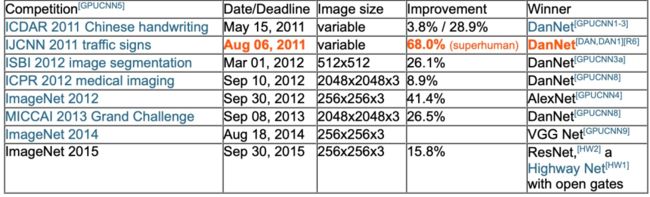
2011年，CNN在ML社区变得更加流行，基于GPU的快速CNN被称为DanNet，它比2006年早期GPU加速的CNN更深更快。2011年，DanNet成为第一个赢得计算机视觉竞赛的纯深度CNN。从2011年到2012年，DanNet享有垄断地位，它赢得了所有的比赛。

1980s-90s:

图神经网络与随机Delta规则（Dropout）

具有快速变化的 "快速权重 "NN被v.d. Malsburg (1981)和其他人引入。可以处理结构化数据的深度学习架构（如图神经网络）在1987年被Pollack提出，并在1990年代早期被Sperduti, Goller和Küchler改进。今天，图神经网络被用于许多应用中。

80年代和90年代还出现了各种在生物学上更合理的深度学习算法的建议，这些算法--与反向传播不同--在空间和时间上都是局部的。1990年，Hanson介绍了随机Delta规则，这是一种通过反向传播训练NN的随机方法。几十年后，这种方法以“dropout ”的形式流行了起来。

1990年2月：

生成式对抗网络/好奇心

生成对抗网络（GANs）于1990年在慕尼黑首次发表，那时被称为人工好奇心。两个对决的NN试图在一个最小极限游戏中使对方的损失最大化。生成器（称为控制器）生成概率输出；预测器（称为世界模型）看到控制器的输出并预测环境对它们的反应。使用梯度下降法，预测器NN将其误差最小化，而生成器NN试图使输出最大化这个误差：一个网的损失就是另一个网的收益。

Schmidhuber的2010年调查将1990年的生成对抗NNs总结如下："作为预测世界模型的神经网络被用来最大化控制器的内在奖励，它与模型的预测误差成正比"。

1991年， Schmidhuber发表了另一种基于两个对抗性NN的ML方法，称为可预测性最小化，用于创建部分冗余数据的分解表示，1996年这种方法应用于图像。

1990年4月：

神经网络生成子目标/按指令工作

近几个世纪以来，大多数NN都致力于简单的模式识别，而非高级推理。高级推理被认为是一个巨大的挑战。然而20世纪90年代初首次出现了转机。学习将复杂的时空观察序列分解成紧凑但有意义的块的NN，以及基于NN的分层行动序列的规划者，用于组合学习。这项工作将传统的 "符号 "层次人工智能的概念注入到端到端的可区分的 "亚符号 "NN中。

1990年，NN学会了用端到端可微分NN的子目标生成器生成层次化的行动计划，用于层次化强化学习（HRL）。之后不久，它学会了生成子目标序列。该系统在多个抽象层次和多个时间尺度上学习行动计划，并解决了最近的 "开放性问题 "。

1991年3月：

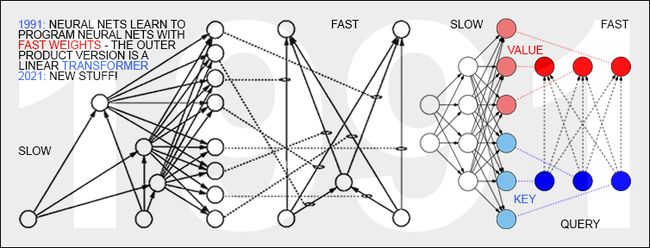
具有线性化自我关注的Transformers

最近，Transformers大行其道。具有 “线性自注意力”的Transformers于1991年3月首次发表。这些所谓的 “快速权重程序员”（Fast Weight Programmers）或“快速权重控制器”（Fast Weight Controllers）以一种端到端差异化、自适应、完全神经的方式分离了存储和控制。标准Transformers中的“自注意力”将其与投射和softmax相结合。

今天的Transformers大量使用无监督预训练，这是Schmidhuber团队1990-1991年的Annus Mirabilis中首次发表的另一种深度学习方法。1991年的快速权重控制器也促成了了元学习的自我参照NN，它们可以对自己运行自己的权重变化算法或学习算法，并改进它的方式等等。

1991年4月：

通过自我监督的预训练进行深度学习

在20世纪90年代之前，基于梯度的训练只对浅层NN有效。这个深度学习问题对于递归NN来说是最明显的。为了通过基于RNN的 "一般深度学习 "来克服这个缺点， Schmidhuber建立了一个自我监督的RNN层次，在多个抽象层次和多个自组织时间尺度上学习表征：神经序列chunker或神经历史压缩器。每个RNN试图解决预测其下一个输入的借口任务，只将意外输入发送给上方的下一个RNN。由此产生的压缩序列表示极大地促进了下游的监督性深度学习，如序列分类。

虽然那时的计算机速度比现在慢一百万倍，但到了1993年，上述的神经历史压缩器已经能够解决以前无法解决的深度>1000的“非常深度学习”任务。

1991年4月：NNs蒸馏程序

使用1991年发表的NN蒸馏程序，上述神经历史压缩器的分层内部表征可以被压缩成一个单一的递归NN（RNN）。这里，“老师”NN的知识被 "蒸馏 "到“学生”NN中，通过训练学生NN来模仿教师NN的行为（同时也重新训练学生NN以前学到的技能，使其不会忘记这些技能）。NN蒸馏法今天被广泛使用。

1991年6月：

基本问题：消失的梯度

Schmidhuber的第一个学生Sepp Hochreiter在1991年的毕业论文中发现并分析了深度学习的基本问题。首先，他实现了上述的压缩器，随后做了更多的工作，并发现深度NN受到现在著名的梯度消失或爆炸问题的困扰：在典型的深度或递归网络中，反向传播的误差信号要么迅速缩小，要么超出界限增长。在这两种情况下，学习都会失败。这一分析导致了现在被称为LSTM的基本原则。

1991年6月：

LSTM、Highway Nets和ResNets的基础

长短期记忆（LSTM）递归神经网络克服了Sepp的基本深度学习问题。通过Felix Gers、Alex Graves和其他人的工作，LSTM及其训练程序在 Schmidhuber在IDSIA的瑞士LSTM资助中得到了进一步的改进。一个里程碑是“vanilla LSTM架构”--1999-2000年的LSTM变体。Alex是第一次成功地将LSTM应用于语音的主要 Schmidhuber（2004年）。2005年首次发表了现在广泛使用的具有完全反向传播的LSTM和双向LSTM。

另一个里程碑是2006年的训练方法：“连接主义时间分类”或CTC，用于同时对齐和识别序列。Schmidhuber团队在2007年成功地将CTC训练的LSTM应用于语音。

1995年：神经概率语言模型

第一个卓越的端到端神经机器翻译也是基于LSTM的。1995年就已经有一个优秀的神经概率文本模型，到2017年，LSTM还为Facebook的机器翻译、苹果的Quicktype、亚马逊的Alexa语音、谷歌的图像标题生成和自动电子邮件回复等提供支持。《商业周刊》称LSTM "是最商业化的人工智能成就。"到2016年，谷歌数据中心用于推理的超强计算能力有四分之一以上用于LSTM。当然，LSTM也被大量用于医疗保健和医疗诊断。

1980s-: 

无师自通的学习行动网络（RL）

NN也与强化学习（RL）有关。一般的RL代理必须发现，在没有“老师”的帮助下，如何与一个动态的、初始未知的、部分可观察的环境互动，以使他们的预期累积奖励信号最大化。RL问题和计算机科学的其他问题一样难，因为任何具有可计算描述的任务都可以在一般的RL框架中被表述出来。

某些RL问题可以通过早在20世纪80年代之前发明的非神经技术来解决。如蒙特卡洛（树）搜索（MC，1949），动态编程（DP，1953）等；深度FNN和RNN也是改进某些类型RL的有用工具。当环境有一个马尔科夫接口，使RL机器的当前输入传达了确定下一个最佳行动所需的所有信息时，基于DP/TD/MC的RL可以非常成功。对于没有马尔科夫界面的复杂情况，学习机不仅要考虑现在的输入，还要考虑以前的输入，因此，RL算法和LSTM的组合已经成为标准。

RL的未来将是对复杂输入流进行紧凑的时空抽象的学习、组合和规划。NN如何学习以分层的方式，在多个抽象层次和多个时间尺度上表示概念和行动计划？Schmidhuber团队在1990-91年发表了这些问题的答案：自我监督的神经历史压缩机学习以多层次的抽象和多时间尺度来表示感知，而基于端到端的可微分NN的子目标生成器通过梯度下降学习层次化的行动计划。

不可忽视的硬件的问题

如果没有持续改进和加速的计算机硬件，最近的深度学习算法的突破不可能实现。任何人工智能和深度学习的历史，如果不提及这种至少已经运行了两千年的演变，都是不完整的。

第一个已知的基于齿轮的计算设备是2000多年前古希腊的Antikythera机制（一种天文钟）。世界上第一台实用的可编程机器应该是1世纪亚历山大的赫伦制造的自动剧院。

9世纪巴格达Banu Musa兄弟的音乐自动机也许是第一台有存储程序的机器。它使用旋转圆筒上的针来存储程序，控制一个蒸汽驱动的长笛。

16世纪出现了更灵活的机器，它们根据输入数据计算出答案。第一台用于简单算术的专用计算器是由威廉-希卡德在1623年制造，他也是“自动计算之父”的候选人之一；1673年，戈特弗里德-威廉-莱布尼茨（Gottfried Wilhelm Leibniz）设计了第一台可以进行四种算术运算的机器（步算机），这也是第一台有内存的机器。

第一台商业程序控制的机器是由Joseph-Marie Jacquard和其他人在1800年左右在法国制造的，他们编写了世界上第一个工业软件。他们启发了艾达-洛夫莱斯和她的导师查尔斯-巴贝奇（英国，约1840年），他计划建立一个可编程的通用计算机（但未成功）。

1914年，西班牙人莱昂纳多-托雷斯-奎维多成为20世纪第一个人工智能的先驱，他建造了第一个工作的国际象棋“终结者”。

1935年至1941年期间，康拉德·楚泽（Konrad Zuse）创造了世界上第一台可用的可编程通用计算机：Z3。1936年的相应专利描述了可编程物理硬件所需的数字电路，比克劳德-香农1937年关于数字电路设计的论文还要早。Zuse使用莱布尼茨的二进制计算原理计算方法，这大大简化了硬件。忽略任何物理计算机不可避免的存储限制，Z3的物理硬件确实是现代意义上的通用的。

第一个电子专用计算器是约翰-阿塔纳索夫（管式计算之父）的二进制ABC（美国，1942）。但与Z3不同，ABC不能自由编程。汤米-弗劳尔斯（Tommy Flowers，1943-45）的电子巨像机也不是用来破解纳粹密码的。

第一台由其他人制造的一般可编程机器是霍华德-艾肯的十进制MARK I（美国，1944）。Eckert和Mauchly（1945/46）制造的更快的十进制ENIAC是通过重新接线来编程的。从那时起，计算机通过集成电路（IC）变得更快。自20世纪70年代以来，图形处理单元（GPU）被用来通过并行处理加快计算速度。今天的IC/GPU包含数十亿个晶体管。

1941年，Z3可以每秒执行大约一个基本操作（例如加法）。从那时起，每隔5年，计算就会便宜10倍。截至2021年，即Z3之后的80年，现代计算机可以以相同的（经通货膨胀调整）价格每秒执行约1000万亿条指令。对这一指数趋势的天真推断预测，21世纪将看到廉价计算机的原始计算能力是所有人类大脑的总和的一千倍。

那么物理层面的极限在哪里？根据Bremermann(1982)的说法，一台质量为1公斤、体积为1升的计算机每秒最多可以在1032位上执行1051次运算。上述趋势将在2200年左右达到Bremermann的极限。然而，由于太阳系中只有2 x 1030公斤的质量，这一趋势必然会在几个世纪内被打破，因为光速将极大地限制获得额外的质量。

物理学似乎决定了未来的高效计算硬件必须像大脑一样，在三维空间里有许多紧凑放置的处理器，通过许多短线和少数长线疏散连接，以最小化总连接成本。基本架构是一个深度、疏散连接的三维RNN，而这种RNN的深度学习方法将变得比今天更加重要。

1931年以来的人工智能理论

现代人工智能和深度学习的核心大多是基于近几个世纪的简单数学：微积分/线性代数/统计学。然而，为了在上一节提到的现代硬件上有效地实现这一核心，并为数十亿人所用，大量的软件也是必要的。这里将列出人工智能和计算机科学理论的一些最重要的亮点。

20世纪30年代初，哥德尔创立了现代理论计算机科学。他引入了一种通用编码语言（1931-34），以整数为基础，并允许以公理形式将任何数字计算机的操作正规化。哥德尔用它来表示数据和程序。他构建了著名的形式化语句，谈论其他形式化语句的计算。他确定了算法性定理证明、计算以及任何类型的基于计算的人工智能的基本限制。

1935年，Alonzo Church通过证明Hilbert & Ackermann的Entscheidungsproblem（决策问题）没有一般的解决方案，得出了哥德尔结果的推论。为了做到这一点，他使用了另一种通用编码语言，称为Untyped Lambda Calculus，它构成了极具影响力的编程语言LISP的基础。1936年，阿兰-图灵引入了另一个通用模型：图灵机。

Konrad Zuse不仅创造了世界上第一台可用的可编程通用计算机，他还设计了Plankalkül，第一种高级编程语言。

1964年，Ray Solomonoff将贝叶斯（实际上是拉普拉斯）概率推理和理论计算机科学结合起来，推导出一种数学上最优（但计算上不可行）的学习方式，从过去的观察中预测未来数据。他与安德烈-科尔莫戈罗夫一起创立了科尔莫戈罗夫复杂性或算法信息理论（AIT）的理论，超越了传统的信息理论，通过计算数据的最短程序的概念，将奥卡姆剃刀的概念正式化。

在21世纪初，Marcus Hutter通过一个最佳行动选择器来增强Solomonoff的通用预测器，用于初始未知但可计算环境中的强化学习代理。他还推导出了所有定义良好的计算问题的渐近最快算法。

尽管如此，由于各种原因，数学上的最优人工智能在实践上还不可行。相反，目前实用的现代人工智能是基于次优的、有限的、但并不被极度理解的技术，如NN和深度学习，但谁知道20年后的人工智能历史会是怎样的呢？

从大爆炸到遥远的未来

让我们将人工智能放到最广泛的历史背景下：自大爆炸至今的所有时间。2014年， Schmidhuber在其中发现了一个美丽的指数加速模式，从那时起，他在许多讲座中介绍了这一模式，它也被录入了Sibylle Berg的获奖书籍《GRM：Brainfuck》。

从人类的角度来看，自宇宙诞生以来的大事件都整齐地排列在一条指数级加速的时间线上。历史似乎将在2040年左右的Omega点上汇合。

从138亿年前的大爆炸开始，把这个时间除以4，得到大约35亿年，地球上出现了生命。

再取这段时间的四分之一，得到9亿年前，类似动物的移动生命出现。

再除以4，得到2.2亿年前，哺乳动物出现。

再到5500万年前，出现了第一批灵长类动物。

1300万年前出现了第一批人类。

再除以4，350万年前，人类发明了第一批石器。

80万年前，出现了下一个伟大的技术突破：火的控制。

20万年前，出现解剖学上特征明显的现代人，他们是我们的祖先。

5万年前，行为上的现代人出现了，我们的祖先，开始在世界范围内殖民。

再除以4，1.3万年前，出现了动物驯化、农业以及第一批定居点，这意味着文明的开始。

3,300年前，进入铁器时代，第一次人口爆炸开始了。

再除以4，由于汇合点Omega是2040年左右，Omega减去800年，即13世纪，铁和火在中国以枪、炮和火箭的形式出现。从那时起，这就决定了世界的发展方向，而西方显然还欠着中国的许可费。

再除以4，Omega减去200年，我们到了19世纪中期，铁和火以更复杂的形式结合在一起，通过改进的蒸汽机为工业革命提供动力；电话开始革新通信；疾病的细菌理论彻底改变了医疗保健，使人们平均寿命更长。大约在1850年，以肥料为基础的农业革命帮助引发了第二次人口爆炸，并在20世纪达到顶峰，当时世界人口翻了两番。

Omega减去50年，这次大约是1990年代，20世纪3场战争，一战、二战和冷战结束。当时7家最有价值的上市公司都是日本公司，而中国和美国西海岸都开始迅速崛起，为21世纪创造了条件。一个数字神经系统开始通过手机和无线革命以及廉价的个人电脑横跨全球。WWW由Tim Berners-Lee在瑞士的欧洲粒子对撞机上创建，现代人工智能也是在这个时候开始的。

再用Omega减去13年，这是不久的将来的一个节点，2030年，那时许多人预测廉价的人工智能将拥有人类的脑力。然后到Omega之前的最后13年左右，届时将发生不可思议的事情，要对这一切抱有信心。

当然，时间不会因为Omega而停止。也许只是人类主导的历史会结束。在Omega点之后，也许许多发现自己目标的元学习AI将迅速改进自己。

超级人工智能会做什么？太空对人类不友好，但对机器人却对友好，而且提供的资源比我们的生物圈薄膜要多得多。虽然一些好奇的人工智能将继续对生命着迷，但大多数人将对机器人和软件生命在太空中的新机会更感兴趣。通过小行星带和其他地方的无数自我复制的机器人工厂，它们将改变太阳系，然后在几十万年内改变整个银河系，在几百亿年内改变可到达的宇宙其他地方。尽管有光速限制，不断扩大的人工智能领域将有足够的时间来殖民和塑造整个可见的宇宙。

现在不妨把思维拉长一点。宇宙还很年轻，只有138亿年的历史。之前我们一直在除以4，现在让我们乘以4，来展望一下宇宙比现在大4倍的时候：那时它大约550亿岁。到那时，可见的宇宙将被智能所渗透。因为在Omega之后，大多数人工智能将不得不去物理资源集中的地方，制造更多更大的人工智能。

更多内容 尽在智源社区公众号