图神经网络对抗攻击(图注入攻击)
paper2:Understanding And Improving Graph Injection Attack By Promoting Unnoticeability (HAO)part1
Abstract
最近,图注入攻击(GIA)作为图神经网络(GNN)上的一种实际攻击场景出现,在这种情况下,攻击只能注入少量恶意节点,而不能修改现有节点或边。即图修改攻击。尽管GIA取得了可喜的成果,但人们对其成功的原因以及成功的背后是否存在任何漏洞知之甚少。为了理解GIA的威力,我们将其与GMA进行了比较,发现GIA由于其相对较高的灵活性,可以证明比GMA更有害。然而,高度的灵活性也会对原始图的同质性分布造成极大的破坏,即邻居之间的相似性。因此,基于同质性的防御系统可以很容易的缓解甚至防止GIA的威胁,这些防御系统目的是恢复原来的同质性。为了缓解这个问题,我们引入了一个新的约束—同质不可察觉性,强制GIA保持同质性,并提出协调对抗目标(Harmonious Adversarial Objective,HAO)来实例化它。大量使用实验表明,使用HAO的GIA可以打破基于同质性的防御,并大大优于以前的攻击。我们相信,我们的方法可以对GNN的健壮性进行更可靠的评估。
尽管取得了令人鼓舞的实证结果,但GIA为何蓬勃发展,以及成功背后是否存在任何缺陷,仍然难以捉摸,为了弥补这一差距,我们通过在统一的环境下将GIA和GMA进行比较来研究GIA的优点和局限性。我们的理论结果表明,在这种情况下,当没有防御时,GIA由于其相对较高的灵活性,可以证明比GMA更有害。这种灵活性使GIA能够将GMA扰动映射为特定GIA扰动,并进一步优化映射的扰动以放大损伤。然而,依据没有免费的午餐定理,我们进一步发现GIA的威力是建立在对原始图的同质性的严重破坏之上的。同质性表示节点连接到具有相似特征或标签的其他节点的趋势,这对于大多数现有的GNN的成功非常重要。同质性的严重损害将使GIA评估健壮性的有效性失效,因为非健壮模型仅通过利用同质性损害的特性就可以轻松的减轻甚至防止GIA。
1、Introduction
图神经网络作为图结构数据的深度学习模型的推广,在涉及关系信息的任务中取得了巨大的成功,然而,GNN在本质上很容易受到敌对攻击,或者输入上的微小故意扰动。先前的研究表明,对输入图的现有拓扑结构或节点特征的适度更改,即图修改攻击(GMA),会显著降低GNN的性能。由于在许多真实世界场景中,修改原始图的成本非常高昂,最近越来越多的人关注图注入攻击(GIA),在这种攻击中,攻击只能注入少量恶意节点来执行攻击。
具体来说,在观察到同质性的破坏之后,很容易设计出一种目的在恢复同质性的防御机制,称之为同质性防御者。同质性防御者对GIA攻击具有很强的鲁棒性。理论上,它们可以有效的将GIA造成的危害降低到低于GMA。从经验上看,通过使用边修剪技术实现同质性防御甚至会恶化最先进的GIA攻击。因此,忽略对同质性的损害将使GIA无能为力,并进一步限制其在评估GNN鲁棒性方面的应用。
为了使GIA能够有效评估各种健壮GNN,在开发GIA时有必要保持同质性。为此,我们引入一种新的约束—同质不可察觉性,可以作为图对抗学习中不可察觉性的补充。为了例证同质不可察觉性,我们提出了HAO。具体来说,HAO通过正则化在攻击期间的同质性分布偏移,引入了同质性约束的一种新的可微实现。这样,同质性防御在进行有效攻击的同时不会轻易识别攻击。在6个基准上对38个防御模型进行了广泛的实验,结果表明,使用HAO的GIA可以突破同质性防御,并在所有环境下显著优于所有以前的工作,包括非目标攻击和目标攻击。我们的贡献总结如下:
- 我们在一个统一的环境中对GIA和GMA进行了形式上的比较,发现GIA由于其高度灵活性,可以证明比GMA更有害。(定理1)
- 然而,GIA的灵活性也会对同质性分布造成严重损害,这使得GIA很容易被同质性防御者防御。(定理2)
- 为了缓解这个问题,我们引入了同质性不可察觉的概念和一个新的目标HAO来进行同质性不可察觉的攻击。(定理3)
2、Preliminaries
1.Graph Neural Networks
考虑一个图 G = ( A , X ) G=(A,X) G=(A,X)具有节点集 V = { v 1 , v 2 , … , v n } V=\{v_1,v_2,\ldots,v_n\} V={v1,v2,…,vn}和边集 E = { e 1 , e 2 , … , e n } E=\{e_1,e_2,\ldots,e_n\} E={e1,e2,…,en}, A ∈ { 0 , 1 } N × N A\in\{0,1\}^{N \times N} A∈{0,1}N×N是邻接矩阵, X ∈ R N × D X\in R^{N \times D} X∈RN×D是节点特征矩阵。我们感兴趣的是节点的半监督节点分类任务。也就是说,给定一组 C C C个类的标签 Y ∈ { 0 , 1 , … , C − 1 } n Y\in\{0,1,\ldots,C-1\}^n Y∈{0,1,…,C−1}n,我们可以训练一个图神经网络 f θ f_\theta fθ通过最小化分类损失 L t r a i n L_{train} Ltrain,在训练(子)图 G t r a i n \mathcal{G}_{train} Gtrain上通过 θ \theta θ参数化(例如交叉熵)。训练好的 f θ f_\theta fθ可以预测测试图 G t e s t \mathcal{G}_{test} Gtest中节点的标签。GNN通常遵循邻居聚合框架,第归的将节点表示更新为:
H u ( k ) = σ ( W k ⋅ ρ ( { H v ( k − 1 ) } ∣ v ∈ N ( u ) ∪ { u } ) ) H _ { u } ^ { ( k ) } = \sigma \left( W _ { k } \cdot \rho \left( \left\{ H _ { v } ^ { ( k - 1 ) } \right\} \mid v \in \mathcal { N } ( u ) \cup \{ u \} \right) \right) Hu(k)=σ(Wk⋅ρ({Hv(k−1)}∣v∈N(u)∪{u}))
N ( u ) \mathcal { N } ( u ) N(u)是节点 u u u邻居的集合, H u ( 0 ) = X u H _ { u } ^ { ( 0) } =X_u Hu(0)=Xu, ∀ u ∈ V \forall u \in V ∀u∈V, H u ( k ) H _ { u } ^ { ( k ) } Hu(k)是第 k k k次聚合节点 u u u的隐藏表示, σ ( ⋅ ) \sigma(\cdot) σ(⋅)是激活函数,比如Relu, ρ ( ⋅ ) \rho(\cdot) ρ(⋅)是对邻居的聚合函数,例如MEAN或者是SUM。
2.Graph Adversarial Attack
图对抗攻击的目标是欺骗GNN模型, f θ ∗ f_{\theta^*} fθ∗,通过构造预算有限的图 G ′ = ( A ′ , X ′ ) G^{\prime}=(A^{\prime},X^{\prime}) G′=(A′,X′),在图 G = ( A , X ) G=(A,X) G=(A,X)上训练,受 ∥ G ′ − G ∥ ≤ Δ \lVert G^{\prime}-G\rVert \leq\Delta ∥G′−G∥≤Δ,给定一组受害节点 V c ⊆ V V_c \subseteq V Vc⊆V,图对抗攻击一般可以表示为:

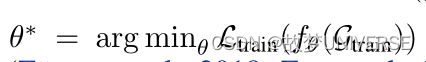
L a t k \mathcal L_{atk} Latk通常被视为 − L t r a i n -\mathcal L_{train} −Ltrain,继之前的工作之后,图对抗攻击可以通过其扰动约束特征化为图修改攻击和图注入攻击。
Graph Modification Attack(GMA)
GMA生成 G ′ G^{\prime} G′通过在原始图上修改图结构 A A A和节点特征 X X X,通常GMA中的约束条件是限制 A A A和 X X X上的扰动数量,分别用 Δ A \Delta_A ΔA和 Δ X \Delta_X ΔX表示:
![]()
X X X上的扰动是以 ϵ \epsilon ϵ的L-p范数为界,因为我们使用的是连续特征。
Graph Injection Attack(GIA)
不同的是,GIA通过注入一组恶意节点生成 G ′ G^{\prime} G′

X a t k X_{atk} Xatk是注入节点的特征, O a t k O_{atk} Oatk是注入节点的邻接矩阵, A a t k A_{atk} Aatk是注入节点和原始节点之间的邻接矩阵,设 d u d_u du表示节点 u u u的度,GIA中的约束为:
![]()
注入节点的数量和度是有限的, D X = { C ∈ R d , m i n ( X ) ⋅ 1 ≤ C ≤ m a x ( X ) ⋅ 1 } \mathcal D_X=\{C\in R^d,min(X)\cdot1\leq C\leq max(X)\cdot1\} DX={C∈Rd,min(X)⋅1≤C≤max(X)⋅1}, m i n ( X ) min(X) min(X)和 m a x ( X ) max(X) max(X)分别是 X X X中最小和最大的条目。
Threat Model
我们采用了一个统一设置,图稳健性基准使用的逃逸,归纳,黑盒。逃逸:攻击发生在测试时间,即 G t e s t G_{test} Gtest,而不是 G t r a i n G_{train} Gtrain.归纳:测试即节点在训练时间不可见。黑盒:攻击无法访问目标模型的体系结构或参数。
3、Power And Pitfalls Of Graph Injection Attack
基于上述设置,将GIA与GMA进行比较,研究GIA的优点和局限性。虽然我们发现在没有防御的情况下,GIA比GMA更有害(定理1),但我们也发现GIA中的陷阱使其更容易防御(定理2)。
3.1 Power Of Graph Injection Attack
根据之前的工作,我们使用线性GNN,即 H ( k ) = A ^ X Θ H^{(k)}=\hat A X \Theta H(k)=A^XΘ,来跟踪攻击带来的变化。首先,将详细阐述攻击的威胁,如下所示:
Definition 3.1(Threats)考虑攻击 A \mathcal A A,给定一个扰动预算 Δ \Delta Δ, A \mathcal A A对GNN f θ f_{\theta} fθ的威胁定义为 m i n ∥ G ′ − G ∥ ≤ Δ min_{\lVert G^{\prime}-G\rVert \leq \Delta} min∥G′−G∥≤Δ L a t k ( f θ ( G ′ ) ) \mathcal L_{atk}(f_{\theta}(G^{\prime})) Latk(fθ(G′))。
根据Definition3.1,我们可以定量的比较不同攻击的威胁。
Theorem 1. 给定适当的扰动预算 Δ G I A \Delta_{GIA} ΔGIA 和 Δ G M A \Delta_{GMA} ΔGMA。让 Δ G I A ≤ Δ G M A ≤ ∣ V ∣ ≤ ∣ E ∣ \Delta_{GIA} \leq \Delta_{GMA} \leq |V|\leq|E| ΔGIA≤ΔGMA≤∣V∣≤∣E∣。对于在 G \mathcal G G上训练的固定的线性GNN f θ f_{\theta} fθ,假设 G \mathcal G G没有孤立节点,GIA和GMA遵循最优策略。 ∀ Δ G M A ≥ 0 \forall \Delta_{GMA}\ge 0 ∀ΔGMA≥0, ∃ Δ G I A ≤ Δ G M A \exist \Delta_{GIA}\leq\Delta_{GMA} ∃ΔGIA≤ΔGMA
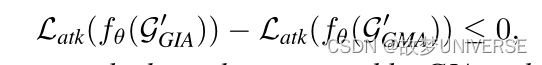
在预算相等或更少的情况下,GIA比GMA损害更大。
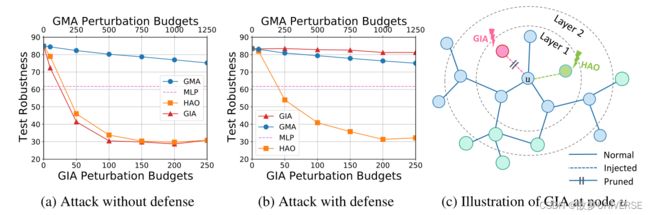
直观来看,GIA的威力主要来自它在扰动生成方面相对较高的灵活性。这种灵活性使我们能够找到一种映射,可以将任何GMA扰动映射到GIA,从而对 f θ f_\theta fθ的预测产生同样的影响,将在下面给出例子:
Definition 3.2 (Plural Mapping M 2 M_2 M2)
M 2 M_2 M2映射通过GMA使用加边扰动为GIA扰动
