《PFLD: A Practical Facial Landmark Detector》论文笔记
PFLD: A Practical Facial Landmark Detector
1. Introduction
人脸特征点检测又称为人脸对齐,旨在自动定位人脸上一组预定义的基准点(如眼角、嘴角等)。人脸对齐作为人脸识别和验证,以及人脸变形和编辑等各种人脸应用的基本组成部分,在过去几年中得到了视觉界的广泛关注,并取得了巨大进步。然而,开发一个实用的人脸特征检测器仍是一个具有挑战性的任务,因为检测器需要同时兼顾检测精度、处理速度以及模型尺寸方面的问题。
在实现世界中,几乎不可能获得完美的人脸。换句话说,人脸经常处于不受控制甚至不受约束的环境中。外貌在不同的光照条件下其姿态,表情及外形都会有明显的差异,有时甚至会出现局部遮挡。上图就显示几个这样的例子。另外,对于数据驱动的方法而言,足够的训练数据是影响模型性能的关键。虽然,通过平衡考虑在不同条件下采样多人面部的方法可能是可行的,但这种收集方式不切实际,尤其是在需要大规模数据来训练(深度)模型时。 在这种情况下,经常会遇到数据不平衡的问题。 下面我们将有关特征点检测的问题归纳为三个挑战。
挑战 # 1 \#1 #1 - 局部变化. 表情、局部极端光照(如高光和阴影)和遮挡会给人脸图像带来部分变化/干扰。 部分区域的特征点可能会偏离正常位置,甚至消失。
挑战 # 2 \#2 #2 - 全局变化. 姿态和成像质量是全局影响图像中人脸外貌的两个主要因素,当人脸的全局结构被错误估计时,这将导致(大部分)特征点定位不佳。
挑战 # 3 \#3 #3 - 数据不平衡. 在浅层学习和深度学习中,可用数据集在其类/属性之间表现出不平衡分布的情况并不少见。 这种不平衡很可能使算法/模型无法正确表示数据的特征,从而不能在不同属性之间提供令人满意的准确性。
上述挑战大大增加了准确检测的难度,要求检测器具有鲁棒性。
随着便携式设备的出现,越来越多的人更愿意随时随地处理业务或娱乐。 因此,模型除追求高检测精度外,还应考虑以下挑战。
挑战 # 4 \#4 #4 - 模型效率. 适用性的另外两个限制方面是模型尺寸和运算需求。 机器人、增强现实和视频聊天等任务被期望在运算和内存资源受限的平台(如智能手机或嵌入式产品)上及时执行。
这一点要求检测器具有较小的模型尺寸和快速的处理速度。毫无疑问,人们希望建立准确、高效、紧凑的实用特征点检测系统。
1.1 Previous Arts
略
1.2 Our Contributions
略
2. Methodology
对于上述挑战,我们需要采取有效措施。在本节中,我们首先关注了损失函数的设计,该函数会同时处理挑战 # 1 \#1 #1, # 2 \#2 #2及 # 3 \#3 #3问题。然后,我们详细介绍了网络结构。整个深度网络由一个用于预测特征点坐标的骨干子网络以及一个用于估计几何信息的辅助子网络组成,其中骨干子网络专门考虑了挑战 # 4 \#4 #4问题。
2.1 Loss Function
训练质量很大程度上取决于损失函数的设计,特别是在训练数据规模不够大的情况下。对于惩罚真实特征点 X : = [ x 1 , … , x N ] ∈ R 2 × N \mathbf{X} := [\mathbf{x}_1,\ldots,\mathbf{x}_N]\in\mathbb {R}^{2\times N} X:=[x1,…,xN]∈R2×N与预测特征点 Y : = [ y 1 , … , y N ] ∈ R 2 × N \mathbf{Y}:=[\mathbf{y}_1,\ldots,\mathbf{y}_N]\in\mathbb {R}^{2\times N} Y:=[y1,…,yN]∈R2×N之间的误差,最简单的方式就是使用 ℓ 1 \ell_1 ℓ1及 ℓ 2 \ell_2 ℓ2损失函数。然而,这种不考虑几何/结构信息,对不同特征点误差等价测量的方式并不明智。例如,给定一对图像空间特征点 x i \mathbf{x}_i xi和 y i \mathbf{y}_i yi,其偏差为 d i : = x i − y i \mathbf{d}_i:=\mathbf{x}_i-\mathbf{y}_i di:=xi−yi,如果使用两种投影(姿态相对于相机)方式将 3 D 3\mathrm{D} 3D真实人脸转换为 2 D 2\mathrm{D} 2D图像,那么真实人脸中的固有偏差在两张图像中会显著不同。因此,将几何信息整合到惩罚过程中有助于缓解这一问题。形式上, X \mathbf{X} X表示 2 D 2\mathrm{D} 2D特征点,是 3 D 3\mathrm{D} 3D人脸特征点的投影, 3 D 3\mathrm{D} 3D人脸特征点使用符号 U ∈ R 4 × N \mathbf{U}\in\mathbb {R}^{4\times N} U∈R4×N表示,其中各列对应一个 3 D 3\mathrm{D} 3D位置 [ u i , v i , z i , 1 ] T [u_i,v_i,z_i,1]^T [ui,vi,zi,1]T。假设使用如文献《 P o s e - I n v a r i a n t Pose\text{-}Invariant Pose-Invariant 3 D 3D 3D F a c e Face Face A l i g n m e n t Alignment Alignment》中提到的弱透视模型,那么 U \mathbf{U} U和 X \mathbf{X} X特征点可以通过一个 2 × 4 2\times 4 2×4的投影矩阵 P \mathbf{P} P进行映射, X = P U \mathbf{X}=\mathbf{P}\mathbf{U} X=PU。该投影矩阵具有六个自由度,包括偏航、横滚、俯仰、缩放及二维平移。在本文中,我们使用了文献《 J o i n t Joint Joint F a c e Face Face D e t e c t i o n Detection Detection a n d and and A l i g n m e n t Alignment Alignment u s i n g using using M u l t i - t a s k Multi\text{-}task Multi-task C a s c a d e d Cascaded Cascaded C o n v o l u t i o n a l Convolutional Convolutional N e t w o r k s Networks Networks》中提出的人脸检测网络,该网络可以良好地检测人脸,被检测到的人脸会经过中心化和标准化处理。像表情这样的局部变化几乎不会影响投影映射。也就是说,投影矩阵可以减少三个自由度,包括缩放及二维平移,因此只需要估计三个欧拉角(偏航、横滚及俯仰)。
此外,在深度学习中,数据不平衡是另一个常常限制检测准确率性能的问题。例如,训练集可能包含大量的正面人脸而缺少那些具有较大姿势的人脸。如果不使用额外的训练技巧,用上述训练集训练的模型几乎肯定是不能很好地处理较大姿势人脸的。在这种情况下,“等价”地惩罚各个样本反而是不平等的。为了解决这个问题,我们主张对稀有训练样本误差的惩罚要大于对丰富训练样本误差的惩罚。
从数学上讲,损失函数可以用以下一般形式表示:
L : = 1 M ∑ m = 1 M ∑ n = 1 N γ n ∥ d n m ∥ \mathcal{L}:=\frac{1}{M} \sum_{m=1}^{M} \sum_{n=1}^{N} \gamma_{n}\left\|\mathbf{d}_{n}^{m}\right\| L:=M1m=1∑Mn=1∑Nγn∥dnm∥
其中 ∥ ⋅ ∥ \|\cdot\| ∥⋅∥表示用于测量第 m m m个输入的第 n n n个特征点和真实特征点之间距离/误差的某种度量方法。 N N N是预先定义的每个人脸要检测的特征点数目。 M M M表示每次处理的训练图像数目。对于给定的度量方法(如本文使用的 ℓ 2 \ell_2 ℓ2度量),权重 γ n \gamma_n γn在损失函数的计算中起着关键作用。综合上述问题,例如几何约束和数据不平衡,新的损失函数设计如下:
L : = 1 M ∑ m = 1 M ∑ n = 1 N ( ∑ c = 1 C ω n c ∑ k = 1 K ( 1 − cos θ n k ) ) ∥ d n m ∥ 2 2 \mathcal{L}:=\frac{1}{M} \sum_{m=1}^{M} \sum_{n=1}^{N}\left(\sum_{c=1}^{C} \omega_{n}^{c} \sum_{k=1}^{K}\left(1-\cos \theta_{n}^{k}\right)\right)\left\|\mathbf{d}_{n}^{m}\right\|_{2}^{2} L:=M1m=1∑Mn=1∑N(c=1∑Cωnck=1∑K(1−cosθnk))∥dnm∥22
很容易看出,上式中的 ∑ c = 1 C ω n c ∑ k = 1 K ( 1 − cos θ n k ) \sum_{c=1}^{C} \omega_{n}^{c} \sum_{k=1}^{K}\left(1-\cos \theta_{n}^{k}\right) ∑c=1Cωnc∑k=1K(1−cosθnk)充当着 γ n \gamma_{n} γn的角色。让我们仔细考察损失函数。其中 θ 1 \theta_1 θ1, θ 2 \theta_2 θ2和 θ 3 \theta_3 θ3( K = 3 K=3 K=3)表示真实人脸偏航、俯仰及横滚角与估计值之间偏差角。显然,随着偏差角的增加,惩罚力度也在增加。此外,我们也将样本使用一个或多个属性类进行标注,包括侧面人脸,正面人脸,抬头,低头,表情及遮挡。权重参数 ω n c \omega_n^c ωnc根据样本类别 c c c的分数进行调整(在本文中参数被简单设置为分数的倒数)。如果禁用几何和数据不平衡的设计,我们的损失函数将会退化为简单的 ℓ 2 \ell_2 ℓ2损失函数。无论 3 D 3\mathrm{D} 3D姿态和/或数据不平衡是否影响训练,我们的损失函数都可以通过其距离测量来处理局部变化的影响。虽然,也有一些文献考虑了使用 3 D 3\mathrm{D} 3D姿态来提高模型性能,但我们的损失函数有以下优点:1)函数耦合了 3 D 3\mathrm{D} 3D姿势与 2 D 2\mathrm{D} 2D距离测量;2)函数很直观,很容易进行向前和向后运算;3)函数使网络以单级而非级联方式进行工作,从而可以提高网络最优性。我们注意到, d n m \mathbf{d}_{n}^{m} dnm变量来自于主干网络,而 θ n k \theta_{n}^{k} θnk变量来自于辅助网络,两个变量使用上述损失函数进行耦合/连接。在接下来的两个小节中,我们详细介绍了我们的网络,其示意说明如下图所示。
2.2. Backbone Network
与其它基于 C N N \mathrm{CNN} CNN的模型相似,我们也采用了多层卷积提取特征及预测特征点。考虑到人脸具有很强的全局结构性,例如眼睛、嘴巴、鼻子等的对称性和空间关系,充分利用这一特性可以帮助模型更精确地定位特征点。因此,我们在模型中使用扩展多尺度特征图而非单尺度特征图。特征图的扩展通过调整卷积操作中的滑动步长实现,扩展后特征图感受野也相应扩大。之后,模型会将多尺度特征图全连接进行特征点预测。主干子网络的详细配置如下表所示。从架构的角度来看,主干网络是简单的。我们主要的目的是验证,采用本文提出的新损失及辅助子网络(在下一小节中讨论),即使使用架构非常简单的主干网络模型也可以实现最先进的性能。
| Input | Operator | t | c | n | s |
|---|---|---|---|---|---|
| 1122x3 | Conv3x3 | - | 64 | 1 | 2 |
| 562x64 | Depthwise Conv3x3 | - | 64 | 1 | 1 |
| 562x64 | Bottleneck | 2 | 64 | 5 | 2 |
| 282x64 | Bottleneck | 2 | 128 | 1 | 2 |
| 142x128 | Bottleneck | 4 | 128 | 6 | 1 |
| 142x128 | Bottleneck | 2 | 16 | 1 | 1 |
| (S1)142x16 | Conv3x3 | - | 32 | 1 | 2 |
| (S2)72x32 | Conv7x7 | - | 128 | 1 | 1 |
| (S3)12x128 | - | - | 128 | 1 | - |
| S1,S2,S3 | Full Connection | - | 136 | 1 | - |
主干网络的处理速度和模型大小是算法性能瓶颈,因为测试过程只涉及该分支。因此,使主干网络快速紧凑是至关重要的。在过去几年的研究中,学术界提出了诸如 S h u f f l e N e t \mathrm{ShuffleNet} ShuffleNet、 B i n a r i z a t i o n \mathrm{Binarization} Binarization及 M o b i l e N e t \mathrm{MobileNet} MobileNet等技术用以加速网络。由于 M o b i l e N e t \mathrm{MobileNet} MobileNet技术(深度可分离卷积、线性瓶颈及反向残差)具有良好的性能,本文使用 M o b i l e N e t \mathrm{MobileNet} MobileNet构建块代替传统卷积操作。使用这种优化方式后,我们的主干网络计算负载显著降低,从而加快了运算速度。另外,我们的网络可以根据用户需求调整 M o b i l e N e t s \mathrm{MobileNets} MobileNets宽度参数压缩模型,使模型更小更快。此调整是基于以下观察和假设进行的:深度卷积层的大量单特征通道可能位于低维流形中。因此,在不(明显)降低精度的情况下减少特征图数目是非常可行的。这再次证实了一个设计良好的简单\小型架构网络可以在人脸特征点检测任务上取得足够好的表现。值得一提的是,量化技术与 S h u f f l e N e t \mathrm{ShuffleNet} ShuffleNet及 M o b i l e N e t \mathrm{MobileNet} MobileNet技术完全兼容,这意味着我们可以通过量化进一步减小模型的大小。
2.3. Auxiliary Network
以往的研究工作表明,适当的辅助约束有利于特征点定位的稳定性及鲁棒性。我们的辅助网络也扮演着这样的角色。与之前的方法不同,例如有的网络会学习 3 D \mathrm{3D} 3D到 2 D \mathrm{2D} 2D的投影矩阵,有的网络会查找树枝状结构,有的网络会使用边界线,我们辅助网络其目标在于估计包括偏航、俯仰、横滚角在内的 3 D 3\mathrm{D} 3D旋转信息。有了这三个欧拉角,头部姿态就可以被确定。
有人可能想知道,给定预测和真实特征点后,为什么不直接由此计算欧拉角?从技术上讲,这是可行的,但在训练之初特征点的预测可能不太准确,这会导致训练进入过度惩罚和缓慢收敛的两难境地。为了将旋转信息估计与特征点定位解耦,我们引入了辅助子网络。
值得一提的是, D e T o n e \mathrm{DeTone} DeTone等人提出了一种用于估计两张相关图像单应性的深度网络。偏航、横滚及俯仰角可以从估计的单应矩阵中计算得出。然而,对于本文的任务,我们并没有每个训练样本的正面人脸图像。有趣的是,我们的辅助网络可以直接输出目标角度而不需要正面人脸图像作为输入。这是由于正面人脸具有很强的规律性和结构性。此外,表情和灯光等因素几乎不影响人脸姿势。因此,平均正面人脸可以用于不同人。换句话说,计算欧拉角不需要额外的辅助信息。我们的计算方法如下:1)预先定义一个标准人脸(从一组正面人脸上取平均值)并且选定 11 11 11个特征点作为所有训练人脸的参考点;2)利用每张人脸 11 11 11个特征点与参考点的对应关系估计旋转矩阵;3) 从旋转矩阵中计算欧拉角。就准确性而言,每张人脸的欧拉角可能不太准确,因为所有的人脸都使用标准人脸作为参考。尽管如此,这些欧拉角对于我们的任务来说已经足够准确了,在后续的实验中也会验证这一点。本文提出的辅助网络配置如下表所示。需要注意的是,辅助网络的输入来自主干网络的第 4 4 4个构建块(见上表)。
| Input | Operator | c | s |
|---|---|---|---|
| 282x64 | Conv3x3 | 128 | 2 |
| 142x128 | Conv3x3 | 128 | 1 |
| 142x128 | Conv3x3 | 32 | 2 |
| 72x32 | Conv7x7 | 128 | 1 |
| 12x128 | Full Connection | 32 | 1 |
| 12x32 | Full Connection | 3 | - |
2.4. Implementation Details
在训练过程中,所有的人脸都会根据预处理给定的边界框裁剪并调整为 112 × 112 112\times 112 112×112的大小。我们使用 K e r a s \mathrm{Keras} Keras框架实现网络,批大小设置为 256 256 256,网络采用 A d a m \mathrm{Adam} Adam技术进行优化,权值衰减设置为 1 0 − 6 10^{-6} 10−6,动量设置为 0.9 0.9 0.9。训练最大迭代次数为 64 K 64\mathrm{K} 64K,学习速率在整个训练过程中都被固定设置为 1 0 − 4 10^{-4} 10−4。整个网络在 N v i d i a \mathrm{Nvidia} Nvidia G T X \mathrm{GTX} GTX 1080 T i 1080\mathrm{Ti} 1080Ti G P U \mathrm{GPU} GPU上进行训练。对于 300 W 300\mathrm{W} 300W数据集,我们采用翻转及按 5 ∘ 5^{\circ} 5∘间隔从 − 3 0 ∘ -30^{\circ} −30∘至 3 0 ∘ 30^{\circ} 30∘旋转图像的方式增强训练数据。此外,每个样本会随机遮挡 20 % 20\% 20%的人脸大小区域。而对于 A F L W \mathrm{AFLW} AFLW数据集,我们直接将原始训练数据输入到网络中,而不采用任何数据增强。测试过程只涉及到主干网络,其效率更高。
3. Experimental Evaluation
3.1. Experimental Settings
数据集. 为了评估我们提出的 P F L D \mathrm{PFLD} PFLD模型性能,我们在两个广泛采用的具有挑战性的数据集上进行实验,即 300 W 300\mathrm{W} 300W及 A F L W \mathrm{AFLW} AFLW。
300 W \mathit{300W} 300W. 该数据集使用 68 68 68个特征点标注了 5 5 5个人脸数据集,包括 L F P W \mathrm{LFPW} LFPW、 A F W \mathrm{AFW} AFW、 H E L E N \mathrm{HELEN} HELEN、 X M 2 V T S \mathrm{XM2VTS} XM2VTS及 I B U G \mathrm{IBUG} IBUG。我们使用 3148 3148 3148张图像进行训练, 689 689 689张图像进行测试。测试图像又分为两个子集,即由来自 L F P W \mathrm{LFPW} LFPW及 H E L E N \mathrm{HELEN} HELEN数据集的 554 554 554张图像组成的普通子集和由来自 I B U G \mathrm{IBUG} IBUG数据集的 135 135 135张图像组成的挑战子集。两个子集共同构成完整的测试集。
A F L W \mathit{AFLW} AFLW. 该数据集由 24386 24386 24386张自然场景下的人脸图像组成,图像来自 F l i c k e r \mathrm{Flicker} Flicker具有夸张的姿势、表情及遮挡。这些人脸的头部偏航角范围由 0 ∘ 0^{\circ} 0∘至 12 0 ∘ 120^{\circ} 120∘,其俯仰及滚转角最大也达到了 9 0 ∘ 90^{\circ} 90∘。 A F L W \mathrm{AFLW} AFLW为每张人脸最多标记 21 21 21个特征点。我们分别使用 20000 20000 20000张图像和 4386 4386 4386张图像进行训练和测试。
竞品. 本文实验对比的方法包括经典的及最近提出的基于深度学习的方案,它们分别是 RCPR(ICCV’13) \text{RCPR(ICCV'13) } RCPR(ICCV’13) , SDM(CVPR’13) \text{SDM(CVPR'13)} SDM(CVPR’13), CFAN(ECCV’14) \text{CFAN(ECCV'14)} CFAN(ECCV’14), CCNF(ECCV’14) \text{CCNF(ECCV'14)} CCNF(ECCV’14), ESR(IJCV’14) \text{ESR(IJCV'14)} ESR(IJCV’14), ERT(CVPR’14) \text{ERT(CVPR'14)} ERT(CVPR’14), LBF(CVPR’14) \text{LBF(CVPR'14)} LBF(CVPR’14), TCDCN(ECCV’14) \text{TCDCN(ECCV'14)} TCDCN(ECCV’14), CFSS(CVPR’15) \text{CFSS(CVPR'15)} CFSS(CVPR’15), 3DDFA(CVPR’16) \text{3DDFA(CVPR'16)} 3DDFA(CVPR’16), MDM(CVPR’16) \text{MDM(CVPR'16)} MDM(CVPR’16), RAR(ECCV’16) \text{RAR(ECCV'16)} RAR(ECCV’16), CPM(CVPR’16) \text{CPM(CVPR'16)} CPM(CVPR’16), DVLN(CVPRW’17) \text{DVLN(CVPRW'17)} DVLN(CVPRW’17), TSR(CVPR’17) \text{TSR(CVPR'17)} TSR(CVPR’17), Binary-CNN(ICCV’17) \text{Binary-CNN(ICCV'17)} Binary-CNN(ICCV’17), PIFA-CNN(ICCV’17) \text{PIFA-CNN(ICCV'17)} PIFA-CNN(ICCV’17), RDR(CVPR’17) \text{RDR(CVPR'17)} RDR(CVPR’17), DCFE(ECCV’18) \text{DCFE(ECCV'18)} DCFE(ECCV’18), SeqMT(CVPR’18) \text{SeqMT(CVPR'18)} SeqMT(CVPR’18), PCDCNN(CVPR’18) \text{PCDCNN(CVPR'18)} PCDCNN(CVPR’18), SAN(CVPR’18) \text{SAN(CVPR'18)} SAN(CVPR’18)及 LAB(CVPR’18) \text{LAB(CVPR'18)} LAB(CVPR’18)。
评估指标. 与之前的研究工作相同,我们也使用归一化平均误差( N M E \mathrm{NME} NME)来测量网络精度,这里的精度指所有带标注特征点归一化误差的平均值。对于 300 W \mathrm{300W} 300W数据集,我们会使用两种归一化因子来分析结果。一种采用眼中心距离作为归一化因子,而另一种采用外眼角距离作为归一化因子。对于 A L F W \mathrm{ALFW} ALFW数据集,由于存在各种侧面人脸,我们采用真实边界框大小对误差进行归一化。同时,我们也采用累积误差分布( C E D \mathrm{CED} CED)曲线对比不同特征点检测方法进行分析。除精度外,我们也对比了处理速度及模型尺寸。
3.2. Experimental Results
| Method | Common | Challenging | Fullset |
|---|---|---|---|
| Inter-pupil Normalization(IPN) | |||
| RCPR | 6.18 | 17.26 | 8.35 |
| CFAN | 5.50 | 16.78 | 7.69 |
| ESR | 5.28 | 17.00 | 7.58 |
| SDM | 5.57 | 15.40 | 7.50 |
| LBF | 4.95 | 11.98 | 6.32 |
| CFSS | 4.73 | 9.98 | 5.76 |
| 3DDFA | 6.15 | 10.59 | 7.01 |
| TCDCN | 4.80 | 8.60 | 5.54 |
| MDM | 4.83 | 10.14 | 5.88 |
| SeqMT | 4.84 | 9.93 | 5.74 |
| RAR | 4.12 | 8.35 | 4.94 |
| DVLN | 3.94 | 7.62 | 4.66 |
| CPM | 3.39 | 8.14 | 4.36 |
| DCFE | 3.83 | 7.54 | 4.55 |
| TSR | 4.36 | 7.56 | 4.99 |
| LAB | 3.42 | 6.98 | 4.12 |
| PFLD 0.25X | 3.38 | 6.83 | 4.02 |
| PFLD 1X | 3.32 | 6.56 | 3.95 |
| PFLD 1X+ | 3.17 | 6.33 | 3.76 |
| Inter-ocular Normalization(ION) | |||
| PIFA-CNN | 5.43 | 9.88 | 6.30 |
| RDR | 5.03 | 8.95 | 5.80 |
| PCD-CNN | 3.67 | 7.62 | 4.44 |
| SAN | 3.34 | 6.60 | 3.98 |
| PFLD 0.25X | 3.03 | 5.15 | 3.45 |
| PFLD 1X | 3.01 | 5.08 | 3.40 |
| PFLD 1X+ | 2.96 | 4.98 | 3.37 |
检测精度. 首先,我们在 300 W \mathrm{300W} 300W数据集上将 P F L D \mathrm{PFLD} PFLD与其他顶尖模型进行了比较。对比结果如上表所示。我们的模型包括 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X, P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X及 P F L D 1 X + \mathrm{PFLD\ 1X+} PFLD 1X+三个版本。 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X和 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X分别表示完整模型和压缩模型,压缩模型的宽度参数( M o b i l e N e t \mathrm{MobileNet} MobileNet构建块)被设置为 0.25 0.25 0.25,两种模型都仅使用 300 W \mathrm{300W} 300W数据集进行训练,而 P F L D 1 X + \mathrm{PFLD\ 1X+} PFLD 1X+表示在 W F L W \mathrm{WFLW} WFLW数据集上额外预训练的完整模型。从下表的结果可以看出,我们的 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型明显优于之前的模型,特别是在更具有挑战性的测试子集上。虽然 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型性能略差于 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X,但其性能仍然比其他竞品模型(包括最近推出的 L A B \mathrm{LAB} LAB、 S A N \mathrm{SAN} SAN及 P C D − C N N \mathrm{PCD-CNN} PCD−CNN)更优。上述对比表明 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X在实际应用中是一个很好的折衷模型,它可以在不牺牲太多精度的情况下减少约 80 % 80\% 80%的模型尺寸。这也证实了深度学习卷积层的大量特征通道可能位于低维流形的假设。与 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X相比, P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型在速度上有很大的提升。而对于 P F L D 1 X + \mathrm{PFLD\ 1X+} PFLD 1X+模型,它进一步扩大了网络的精度裕度。上述结果表明我们的网络可以通过输入更多的训练数据来实现改进。
| Model | SDM | SAN | LAB | PFLD 0.25X | PFLD 1X |
|---|---|---|---|---|---|
| Size(Mb) | 10.1 | 270.5+528 | 50.7 | 2.1 | 12.5 |
| Speed | 16ms(C) | 343ms(G) | 2.6s(C)/60ms(G*) | 1.2ms(C)/1.2ms(G)/7ms(A) | 6.1ms(C)/3.5ms(G)/26.4ms(A) |
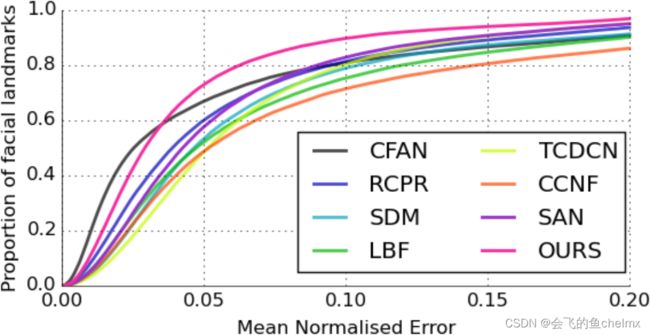
此外,在下图中我们提供了 C E D \mathrm{CED} CED曲线来评估模型性能差异。从更实用的角度来看,不同于之前的对比(人脸边界框真实值根据人脸特征点真实值构建),该对比实验各竞品人脸由 300 W \mathrm{300W} 300W检测器检测。与使用真实边界框相比,一些方案会存在性能下降的问题,例如 S A N \mathrm{SAN} SAN,这与人脸特征点检测器稳定性受人脸检测器影响有关。从曲线上我们可以看出, P F L D \mathrm{PFLD} PFLD模型的性能远优于其他竞品。
我们也进一步评估了不同模型在 A F L W \mathrm{AFLW} AFLW数据集上的性能差异。下表列出了不同竞品方案的 N M E \mathrm{NME} NME结果。从表中可以看出, T S R \mathrm{TSR} TSR、 C P M \mathrm{CPM} CPM、 S A N \mathrm{SAN} SAN以及我们的 P F L D \mathrm{PFLD} PFLD模型明显优于其他竞品。在 T S R M C P M \mathrm{TSRM\ CPM} TSRM CPM, S A N \mathrm{SAN} SAN以及 P F L D \mathrm{PFLD} PFLD模型当中,我们的 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型能实现最优的性能( N M E 1.88 \mathrm{NME\ 1.88} NME 1.88), S A N \mathrm{SAN} SAN次之( N M E 1.91 \mathrm{NME\ 1.91} NME 1.91)。排名第三的是我们的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X,其 N M E \mathrm{NME} NME性能为 2.07 2.07 2.07。需要强调的是, P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型其尺寸大小以及处理速度远远优于 S A N \mathrm{SAN} SAN模型,详见上表。
| Method | RCPR | CDM | SDM | ERT | LBF | CFSS | CCL |
|---|---|---|---|---|---|---|---|
| AFLW | 5.43 | 3.73 | 4.05 | 4.35 | 4.25 | 3.92 | 2.72 |
| Method | Binary-CNN | PCD-CNN | TSR | CPM | SAN | PFLD 0.25X | PFLD 1X |
| AFLW | 2.85 | 2.40 | 2.17 | 2.33 | 1.91 | 2.07 | 1.88 |
模型尺寸. 上上表从模型尺寸以及处理速度方面将我们的 P F L D \mathrm{PFLD} PFLD模型与一些经典或最新的深度学习方法进行了比较。至于模型尺寸,我们的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型仅 2.1 M b \mathrm{2.1Mb} 2.1Mb,与 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X相比节省了 10 M b \mathrm{10Mb} 10Mb以上。 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型与其他模型相比明显更小,例如 S D M 10.1 M b \mathrm{SDM\ 10.1Mb} SDM 10.1Mb, L A B 50.7 M b \mathrm{LAB\ 50.7Mb} LAB 50.7Mb以及 S A N \mathrm{SAN} SAN约 800 M b \mathrm{800Mb} 800Mb(包含两个基于 V G G \mathrm{VGG} VGG的子网络 270.5 M b + 528 M b \mathrm{270.5Mb}+\mathrm{528Mb} 270.5Mb+528Mb)。
处理速度. 此外,我们在 i 7 − 6700 K C P U \mathrm{i7-6700K\ CPU} i7−6700K CPU(用符号 C \mathrm{C} C表示)和 N v i d i a G T X 1080 T i G P U \mathrm{Nvidia\ GTX\ 1080Ti\ GPU} Nvidia GTX 1080Ti GPU(用符号 G \mathrm{G} G表示)上评估了各个模型的运行效率。因为 S D M \mathrm{SDM} SDM和 S A N \mathrm{SAN} SAN模型仅有 C P U \mathrm{CPU} CPU及 G P U \mathrm{GPU} GPU版本是公开的,所以我们仅统计它们在相应设备上的运行时间。至于 L A B \mathrm{LAB} LAB模型,其项目页面上仅能下载 C P U \mathrm{CPU} CPU版本。但是,在 L A B \mathrm{LAB} LAB模型的论文中,作者表示算法在 T I T A N X G P U \mathrm{TITAN\ X\ GPU} TITAN X GPU(用符号 G ∗ \mathrm{G^*} G∗表示)上耗时约 60 m s \mathrm{60ms} 60ms。从对比中可以看出,我们的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X和 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型在 C P U \mathrm{CPU} CPU和 G P U \mathrm{GPU} GPU上的处理速度明显快于其他竞品。需要注意的是, L A B \mathrm{LAB} LAB模型的 C P U \mathrm{CPU} CPU时间以秒为单位而非毫秒。本文提出的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型在 C P U \mathrm{CPU} CPU和 G P U \mathrm{GPU} GPU上耗时相同( 1.2 m s \mathrm{1.2ms} 1.2ms),这是因为大部分时间被消耗到了 I \ O \mathrm{I\backslash O} I\O操作上。另外, P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型在 C P U \mathrm{CPU} CPU上的耗时是 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型的 5 5 5倍,在 G P U \mathrm{GPU} GPU上是 3 3 3倍。尽管如此, P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型任然快过其他竞品。此外,对于 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X和 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型,我们也在 Q u a l c o m m A R M 845 \mathrm{Qualcomm\ ARM\ 845} Qualcomm ARM 845处理器(在表格中用符号 A \mathrm{A} A表示)上测试了它们的性能。 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型每张人脸耗时 7 m s \mathrm{7ms} 7ms(超过 140 f p s \mathrm{140\ fps} 140 fps帧率)而 P F L D 1 X \mathrm{PFLD\ 1X} PFLD 1X模型每张人脸耗时 26.4 m s \mathrm{26.4ms} 26.4ms(超过 37 f p s \mathrm{37\ fps} 37 fps帧率)。
消融实验. 为了验证本文损失函数的优越性,我们在 300 W \mathrm{300W} 300W和 A F L W \mathrm{AFLW} AFLW数据集上进行了消融实验。实验涉及到两种典型的损失函数,包括 ℓ 1 \ell_1 ℓ1和 ℓ 2 \ell_2 ℓ2。如下表所示, ℓ 2 \ell_2 ℓ2和 ℓ 1 \ell_1 ℓ1损失函数的性能差异并不明显,在 300 W \mathrm{300W} 300W数据集上其 I P N \mathrm{IPN} IPN指标分别为[ 4.40 v s . 4.35 4.40\ \mathrm{vs.}\ 4.35 4.40 vs. 4.35],在 A F L W \mathrm{AFLW} AFLW数据集上其 N M E \mathrm{NME} NME指标分别为[ 2.33 v s . 2.31 2.33\ \mathrm{vs.}\ 2.31 2.33 vs. 2.31]。值得注意的是我们的基础损失函数为 ℓ 2 \ell_2 ℓ2。我们考虑了三种损失函数配置:仅具有几何约束的 ℓ 2 \ell_2 ℓ2( ω c = 1 \omega^c=1 ωc=1,使用符号 Ours w/o ω \textbf{Ours w/o}\ \omega Ours w/o ω表示),仅具有加权策略的 ℓ 2 \ell_2 ℓ2( θ k = 0 \theta^k=0 θk=0,禁用辅助网络,使用符号 Ours w/o θ \textbf{Ours w/o}\ \theta Ours w/o θ表示),以及同时具有几何约束和加权策略的 ℓ 2 \ell_2 ℓ2(用符号 Ours \textbf{Ours} Ours表示)。从数值结果可以看出, Ours w/o θ \textbf{Ours w/o}\ \theta Ours w/o θ和 Ours w/o ω \textbf{Ours w/o}\ \omega Ours w/o ω两种配置都可以提升 ℓ 2 \ell_2 ℓ2损失函数性能,在 300 W \mathrm{300W} 300W数据集上分别提高了 4.1 % 4.1\% 4.1%( I P N 4.22 \mathrm{IPN}\ 4.22 IPN 4.22)和 5.9 % 5.9\% 5.9%( I P N 4.14 \mathrm{IPN\ 4.14} IPN 4.14),在 A F L W \mathrm{AFLW} AFLW数据集上分别提高了 4.3 % 4.3\% 4.3%( N M E 2.23 \mathrm{NME\ 2.23} NME 2.23)和 7.3 % 7.3\% 7.3%( N M E 2.16 \mathrm{NME\ 2.16} NME 2.16)。综合考虑几何信息和加权技巧,我们的算法在 300 W \mathrm{300W} 300W和 A F L W \mathrm{AFLW} AFLW数据集上分别提高了 10.2 % 10.2\% 10.2%( I N P 3.95 \mathrm{INP\ 3.95} INP 3.95)和 19.3 % 19.3\% 19.3%( N M E 1.88 \mathrm{NME\ 1.88} NME 1.88)的性能。本实验验证了我们损失函数的有效性。
IPN \textbf{IPN} IPN: 瞳孔间距归一化误差, e i = ∣ ∣ x p r e i − x g t i ∣ ∣ 2 d I P D e_i=\frac{||x_{prei}-x_{gti}||_2}{d_{IPD}} ei=dIPD∣∣xprei−xgti∣∣2。
NME \textbf{NME} NME: N N N个人脸特征点基于 ION \text{ION} ION或 IPN \text{IPN} IPN的平均误差, e = ∑ i = 1 N ∣ ∣ x p r e i − x g t i ∣ ∣ 2 N × d × 100 % e=\frac{\sum_{i=1}^N||x_{prei}-x_{gti}||_2}{N\times d}\times 100\% e=N×d∑i=1N∣∣xprei−xgti∣∣2×100%。
| Loss | l2 | l1 | Ours w/o w | Ours w/o θ | Ours |
|---|---|---|---|---|---|
| 300W(IPN) | 4.40 | 4.35 | 4.22 | 4.14 | 3.95 |
| AFLW(NME) | 2.33 | 2.31 | 2.23 | 2.16 | 1.88 |
其他结果. 上图显示了本文模型在 300 W \mathrm{300W} 300W和 A F L W \mathrm{AFLW} AFLW数据集上的一些可视化结果。这些人脸包括不同的姿态、光照、表情、遮挡、化妆及风格。我们的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型可以获得非常令人满意的特征点定位结果。为了保证系统的完整性,我们首先会使用 M T C N N \mathrm{MTCNN} MTCNN模型对图像/视频帧中的人脸进行检测,然后将检测到的人脸输入 P F L D \mathrm{PFLD} PFLD模型进行特征点定位。在下图中,我们给出了两个包含多张人脸的可视化结果。在第二张照片中,后排有两张人脸被漏检掉了,因为它们被严重遮挡了,很难被检测到。这些漏检是由人脸检测器造成的而非特征点检测器。所有被检测到的人脸其特征点都被很好地计算了。
4. Concluding Remarks
人脸特征点检测系统能否胜任大规模及实时任务需要从三个方面考虑:准确率、效率和紧凑性。本文提出了一种实用的人脸特征点检测算法 P F L D \mathrm{PFLD} PFLD,它由主干网及辅助网两个子网组成。主干网由 M o b i l e N e t \mathrm{MobileNet} MobileNet构建块组成,大大减轻了卷积层的计算压力,而且通过调整构建块宽度参数,模型也对于用户需求有一定的灵活性。多尺度全连通层的引入,扩大了人脸的感受野,提高了模型对人脸结构的捕捉能力。为了进一步调整特征点定位,我们设计了另一个分支,即辅助网络,通过该网络我们可以有效地估计旋转信息。考虑到几何正则化以及数据不平衡的问题,我们设计了一种全新的损失函数。大量的实验结果表明,我们的设计在精度,模型尺寸以及处理速度方面对比其他行业领先方法有卓越的性能,也说明了我们的 P F L D 0.25 X \mathrm{PFLD\ 0.25X} PFLD 0.25X模型在实际应用中是一个很好的折衷方案姿态。
在当前的版本中, P F L D \mathrm{PFLD} PFLD模型训练仅采用了旋转信息(偏航角、横滚角和俯仰角)作为几何约束。若采用其他几何/结构信息预计可进一步提高模型精度。例如,与 L A B \mathrm{LAB} LAB模型类似,我们可以调整特征点使其不偏离边界框太远。从另一个角度看,提升性能也可以从替换基础损失函数角度入手,例如将 ℓ 2 \ell_2 ℓ2替换为特定任务损失函数。在损失函数中设计更复杂的加权策略也将是有益的,特别是在训练数据不平衡和有限的情况下。以上是我们将来工作的优化思路。