OpenCV Sobel算子解析笔记

1. Sobel算子数学原理

1.1 Sobel算子定义

$\text{Sobel}$算子：是计算机视觉领域的一种重要处理方法，主要用于获取数字图像的一阶梯度。该算子包含两组$3\times 3$矩阵，将分别将其与图像作平面卷积，可得到图像$x$方向及$y$方向一阶梯度：
G x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] ∗ I , G y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] ∗ I \mathbf{G}_x=\begin{bmatrix}-1&0&1\\-2&0&2\\-1&0&1\end{bmatrix}*\mathbf{I},\mathbf{G}_y=\begin{bmatrix}-1&-2&-1\\0&0&0\\1&2&1\end{bmatrix}*\mathbf{I} Gx​= ​−1−2−1​000​121​ ​∗I,Gy​= ​−101​−202​−101​ ​∗I

1.2 Sobel算子公式推导

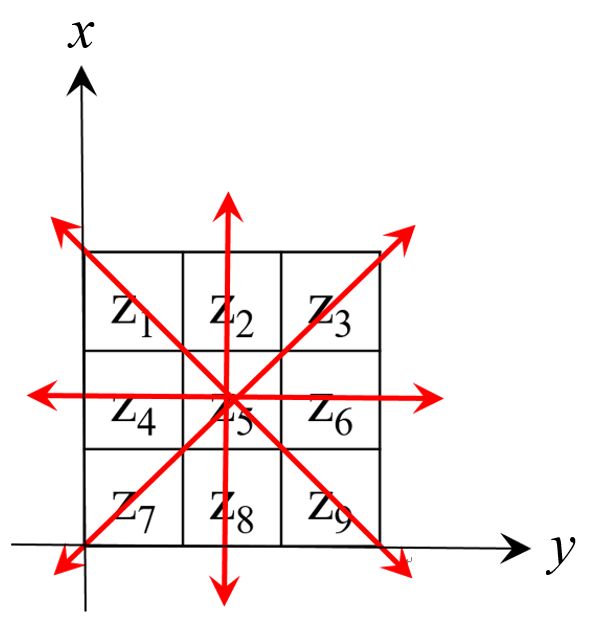
我们考察图像中某$1$个像素点${\text{Z}}_5$及其领域的$8$个像素点，如下图所示：

对于给定领域方向梯度矢量$\mathbf{g}$的幅度为：
$$|\mathbf{g}|=\frac{像素灰度差分}{像素距离}$$
$\text{Sobel}$算子所定义的像素距离为城市距离，如下图所示：

城市距离：在数字栅格中，如果只允许横向和纵向移动，城市距离表示从起点移动到终点所需的最少的步数。

关于像素点${\text{Z}}_5$的方向梯度矢量，可对其$8$领域的水平、垂直和$2$个对角共计$4$个方向对的梯度加权求和：
$$\mathbf{G}=\frac{({\text{Z}}_3-{\text{Z}}_7)}{4}\ast \left[\begin{array}{cc}1& 1\end{array}\right]+\frac{({\text{Z}}_1-{\text{Z}}_9)}{4}\ast \left[\begin{array}{cc}-1& 1\end{array}\right]+\frac{({\text{Z}}_2-{\text{Z}}_8)}{2}\ast \left[\begin{array}{cc}0& 1\end{array}\right]+\frac{({\text{Z}}_3-{\text{Z}}_7)}{2}\ast \left[\begin{array}{cc}1& 0\end{array}\right]$$
其中$4$个向量控制差分方向，系数$\frac{1}{4}$，$\frac{1}{2}$为像素城市距离反比，整理上式可得：
$$\mathbf{G}=\left[\begin{array}{cc}\frac{-{\text{Z}}_1+{\text{Z}}_3-2{\text{Z}}_4+2{\text{Z}}_6-{\text{Z}}_7+{\text{Z}}_9}{4}& \frac{{\text{Z}}_1+2{\text{Z}}_2+{\text{Z}}_3-{\text{Z}}_7-2{\text{Z}}_8-{\text{Z}}_9}{4}\end{array}\right]$$

上述公式推导来自文献https://blog.sciencenet.cn/blog-425437-1139187.html，但$4$个控制差分方向的向量并非全部为单位向量，此处存在一些推理问题。如果将像素距离定义为欧式距离，并将$4$个控制差分方向的向量归一化，那么整理后的方向梯度矢量也与上述公式完全一致。

注意，上式需除以$4$才是平均方向梯度矢量。在实际操作过程中，上式会扩大$4$倍以将计算中的浮点数乘法运算转化为整数乘法运算。因此，计算出的估计值比平均梯度在数值上扩大了$16$倍。调整后的方向梯度矢量的$x$以及$y$分量分别为：
$$\begin{array}{rl}{\text{G}}_x^{\prime }& =-{\text{Z}}_1+{\text{Z}}_3-2{\text{Z}}_4+2{\text{Z}}_6-{\text{Z}}_7+{\text{Z}}_9\\ {\text{G}}_y^{\prime }& ={\text{Z}}_1+2{\text{Z}}_2+{\text{Z}}_3-{\text{Z}}_7-2{\text{Z}}_8-{\text{Z}}_9\end{array}$$
上式与$1.1$节中的$\text{Sobel}$算子定义完全一致。

1.3 高阶Sobel算子

根据算子的对称性以及卷积的运算性质，基础$\text{Sobel}$算子可分解为两次卷积操作：
[ − 1 0 1 − 2 0 2 − 1 0 1 ] = [ 1 2 1 ] ∗ [ − 1 0 1 ] , [ − 1 − 2 − 1 0 0 0 1 2 1 ] = [ 1 2 1 ] ∗ [ − 1 0 1 ] \begin{aligned} \begin{bmatrix}-1&0&1\\-2&0&2\\-1&0&1\end{bmatrix}=\begin{bmatrix}1\\2\\1\end{bmatrix}*\begin{bmatrix}-1&0&1\end{bmatrix}, \begin{bmatrix}-1&-2&-1\\0&0&0\\1&2&1\end{bmatrix}=\begin{bmatrix}1&2&1\end{bmatrix}*\begin{bmatrix}-1\\0\\1\end{bmatrix} \end{aligned} ​−1−2−1​000​121​ ​= ​121​ ​∗[−1​0​1​], ​−101​−202​−101​ ​=[1​2​1​]∗ ​−101​ ​​
观察上式中的两种一维算子可知：$\left[\begin{array}{ccc}1& 2& 1\end{array}\right]$算子或其转置负责像素平滑，而$\left[\begin{array}{ccc}-1& 0& 1\end{array}\right]$算子或其转置负责差分计算。

根据上述分析，对于高阶算子而言，我们分别计算其平滑算子以及差分算子即可。

关于平滑算子，我们采用高斯平滑算子，该算子被认为是一种最优平滑算子。此处我们使用二项式展开式的系数来对高斯算子进行整数近似。对于$n$阶$\text{Sobel}$算子，我们取二项式$n-1$的展开式系数来计算平滑系数。另外，也可以采用$\text{Pascal}$三角来计算平滑系数，平滑算子的$\text{Pascal}$三角形式如下：
$$\begin{array}{cccccccccc}阶数& & & & & & & & & \\ 2& & & & 1& & 1& & & \\ 3& & & 1& & 2& & 1& & \\ 4& & 1& & 3& & 3& & 1& \\ 5& 1& & 4& & 6& & 4& & 1\end{array}$$
三角中各个位置系数计算公式如下：
$$\text{smooth}(n,k)=\frac{(n-1)!}{(n-1-k)!k!}$$
其中，$n$表示$\text{Sobel}$算子阶数，$k$表示系数索引。

关于差分算子，我们取二项式$n-2$的展开式系数两侧补零后的后向差分结果来计算差分系数。也可以采用$\text{Pascal}$三角来计算差分系数，差分算子的$\text{Pascal}$三角形式如下：
$$\begin{array}{cccccccccc}阶数& & & & & & & & & \\ 2& & & & 1& & -1& & & \\ 3& & & 1& & 0& & -1& & \\ 4& & 1& & 1& & -1& & 1& \\ 5& 1& & 2& & 0& & -2& & -1\end{array}$$
三角中各个位置系数计算公式如下：
$$\begin{array}{rl}& \text{Pascal}(n,k)=\{\begin{array}{cc}\frac{n!}{(n-k)!k!}& ,0\le k\le n\\ 0& \end{array}\\ & \text{diff}(n,k)=\text{Pascal}(n-2,k)-\text{Pascal}(n-2,k-1)\end{array}$$
其中，$n$表示$\text{Sobel}$算子阶数，$k$表示系数索引。

2. Sobel算子代码解析

在$\text{OpenCV}$中，关于$\text{Sobel}$算子的核心代码位于$\text{deriv.cpp}$文件中：

void cv::Sobel( InputArray _src, OutputArray _dst, int ddepth, int dx, int dy,
                int ksize, double scale, double delta, int borderType )
                                                                // _src：输入图像
                                                                // _dst：输出图像
                                                                // ddepth：输出图像矩阵类型
                                                                // dx：x方向阶数
                                                                // dy：y方向阶数
                                                                // ksize：算子阶数
                                                                // scale：算子缩放因子
                                                                // delta：在存储滤波结果之前添加到滤波结果中的偏移量
                                                                // borderType：边缘处理类型
{
    CV_INSTRUMENT_REGION();

    CV_Assert(!_src.empty());                                   // 参数检查

    int stype = _src.type(), sdepth = CV_MAT_DEPTH(stype), cn = CV_MAT_CN(stype);
                                                                // stype：矩阵类型，sdepth：数据类型以及数据位数，cn：通道数
    if (ddepth < 0)                                             // 如果输出图像未定义数据类型以及数据位数，则使用输入图像值
        ddepth = sdepth;
    int dtype = CV_MAKE_TYPE(ddepth, cn);                       // 设置输出图像矩阵类型
    _dst.create( _src.size(), dtype );                          // 创建与输入图像同尺寸输出图像

    int ktype = std::max(CV_32F, std::max(ddepth, sdepth));

    Mat kx, ky;
    getDerivKernels( kx, ky, dx, dy, ksize, false, ktype );     // 获取 Sobel 算子系数
    if( scale != 1 )                                            // 如果算子缩放因子不为 1 则对系数进行缩放
    {
        // usually the smoothing part is the slowest to compute,
        // so try to scale it instead of the faster differentiating part
        if( dx == 0 )
            kx *= scale;
        else
            ky *= scale;
    }

    CV_OCL_RUN(ocl::isOpenCLActivated() && _dst.isUMat() && _src.dims() <= 2 && ksize == 3 &&
               (size_t)_src.rows() > ky.total() && (size_t)_src.cols() > kx.total(),
               ocl_sepFilter3x3_8UC1(_src, _dst, ddepth, kx, ky, delta, borderType));
                                                                // OpenCL 加速

    CV_OCL_RUN(ocl::isOpenCLActivated() && _dst.isUMat() && _src.dims() <= 2 && (size_t)_src.rows() > kx.total() && (size_t)_src.cols() > kx.total(),
               ocl_sepFilter2D(_src, _dst, ddepth, kx, ky, Point(-1, -1), delta, borderType))
                                                                // OpenCL 加速

    Mat src = _src.getMat();
    Mat dst = _dst.getMat();

    Point ofs;
    Size wsz(src.cols, src.rows);
    if(!(borderType & BORDER_ISOLATED))
        src.locateROI( wsz, ofs );

    CALL_HAL(sobel, cv_hal_sobel, src.ptr(), src.step, dst.ptr(), dst.step, src.cols, src.rows, sdepth, ddepth, cn,
             ofs.x, ofs.y, wsz.width - src.cols - ofs.x, wsz.height - src.rows - ofs.y, dx, dy, ksize, scale, delta, borderType&~BORDER_ISOLATED);
                                                                // CV_HAL_ERROR_NOT_IMPLEMENTED

    CV_OVX_RUN(true,
               openvx_sobel(src, dst, dx, dy, ksize, scale, delta, borderType))
                                                                // OpenVX 加速

    //CV_IPP_RUN_FAST(ipp_Deriv(src, dst, dx, dy, ksize, scale, delta, borderType));

    sepFilter2D(src, dst, ddepth, kx, ky, Point(-1, -1), delta, borderType );
                                                                // 对 src 图像进行可分离线性滤波
                                                                // src：输入图像
                                                                // dst：输出图像
                                                                // ddepth：输出图像矩阵类型
                                                                // kx：x 方向滤波系数
                                                                // ky：y 方向滤波系数
                                                                // Point(-1, -1)：内核中的锚点位置，默认值 (-1,-1) 表示锚点位于内核中心
                                                                // delta：在存储滤波结果之前添加到滤波结果中的偏移量
                                                                // borderType：边缘处理类型
}

void cv::getDerivKernels( OutputArray kx, OutputArray ky, int dx, int dy,
                          int ksize, bool normalize, int ktype )
{
    if( ksize <= 0 )
        getScharrKernels( kx, ky, dx, dy, normalize, ktype );
    else
        getSobelKernels( kx, ky, dx, dy, ksize, normalize, ktype );
}

static void getSobelKernels( OutputArray _kx, OutputArray _ky,
                             int dx, int dy, int _ksize, bool normalize, int ktype )
                                                                // _kx：x 方向算子系数
                                                                // _ky：y 方向算子系数
                                                                // dx：x 方向算子阶数
                                                                // dy：y 方向算子阶数
                                                                // _ksize：算子阶数
                                                                // normalize：算子系数是否归一化
                                                                // ktype：算子数据类型
{
    int i, j, ksizeX = _ksize, ksizeY = _ksize;
    if( ksizeX == 1 && dx > 0 )                                 // 如果 x 方向需要计算差分且 x 方向算子阶数为1，则调整算子阶数为3
        ksizeX = 3;
    if( ksizeY == 1 && dy > 0 )                                 // 如果 y 方向需要计算差分且 y 方向算子阶数为1，则调整算子阶数为3
        ksizeY = 3;

    CV_Assert( ktype == CV_32F || ktype == CV_64F );            // 参数检查

    _kx.create(ksizeX, 1, ktype, -1, true);                     // 创建 x 方向算子系数
    _ky.create(ksizeY, 1, ktype, -1, true);                     // 创建 y 方向算子系数
    Mat kx = _kx.getMat();
    Mat ky = _ky.getMat();

    if( _ksize % 2 == 0 || _ksize > 31 )                        // 如果算子阶数为偶数或大于31则报错
        CV_Error( CV_StsOutOfRange, "The kernel size must be odd and not larger than 31" );
    std::vector kerI(std::max(ksizeX, ksizeY) + 1);        // 临时算子系数，用于递推 Pascal 三角

    CV_Assert( dx >= 0 && dy >= 0 && dx+dy > 0 );               // 参数检查

    for( int k = 0; k < 2; k++ )
    {
        Mat* kernel = k == 0 ? &kx : &ky;                       // 算子系数
        int order = k == 0 ? dx : dy;                           // 差分阶数
        int ksize = k == 0 ? ksizeX : ksizeY;                   // 算子阶数

        CV_Assert( ksize > order );                             // 参数检查

        if( ksize == 1 )                                        // 算子阶数为1，则算子系数为（1）
            kerI[0] = 1;
        else if( ksize == 3 )                                   // 算子阶数为3
        {
            if( order == 0 )                                    // 如果差分阶数为0，则算子系数为（1，2，1），用于平滑结果
                kerI[0] = 1, kerI[1] = 2, kerI[2] = 1;
            else if( order == 1 )                               // 如果差分阶数为1，则算子系数为（-1，0，1），用于计算一阶差分
                kerI[0] = -1, kerI[1] = 0, kerI[2] = 1;
            else                                                // 如果差分阶数大于1，则算子核为（1，-2，1），用于计算二阶差分
                kerI[0] = 1, kerI[1] = -2, kerI[2] = 1;
        }
        else
        {
            int oldval, newval;
            kerI[0] = 1;
            for( i = 0; i < ksize; i++ )
                kerI[i+1] = 0;

            for( i = 0; i < ksize - order - 1; i++ )            // 递推平滑算子 Pascal 三角
            {
                oldval = kerI[0];
                for( j = 1; j <= ksize; j++ )
                {
                    newval = kerI[j]+kerI[j-1];
                    kerI[j-1] = oldval;
                    oldval = newval;
                }
            }

            for( i = 0; i < order; i++ )                        // 递推差分算子 Pascal 三角
            {
                oldval = -kerI[0];
                for( j = 1; j <= ksize; j++ )
                {
                    newval = kerI[j-1] - kerI[j];
                    kerI[j-1] = oldval;
                    oldval = newval;
                }
            }
        }

        Mat temp(kernel->rows, kernel->cols, CV_32S, &kerI[0]);
        double scale = !normalize ? 1. : 1./(1 << (ksize-order-1));
        temp.convertTo(*kernel, ktype, scale);
    }
}

}