搜索树结点数的估计(回溯法)
在做复杂性分析的时候,采取的都是上界,但是要做实际的估计就不是这样的。比如在搜索的时候着色问题根据图的结构的不同,真正在做调色的时候调色空间大小其实是不太好估计的,搜索空间的树,到底有多少个搜索结点需要搜索,到底有多大,因为中间有剪枝,剪枝又与图有关系,所以这个时候不太好做精确的估计的,这个时候可以采取的办法叫做蒙特卡洛搜索法。
文章目录
-
- 一、Monte Carlo方法
-
- 1、 从根开始,随机选择一条路经
- 2、假定搜索树的其他 ∣ S i ∣ − 1 | S_i | −1 ∣Si∣−1个分支与以上随机选出的路径一样,计数搜索树的点数.
- 3、 重复步骤1 和2,将结点数进行概率平均
- 二、伪码
- 三、4后搜索树遍历的结点
-
- 1、随机选择路径1
- 2、随机选择路径2
- 3、随机选择路径3
- 4、估计结果
- 四、实例
-
- 1、一次抽样
- 2、子过程的伪码
- 五、总结
-
- 1、目的:估计搜索树真正访问结点数
- 2、步骤: 随机抽样,选择一条路径
一、Monte Carlo方法
随机的选择一些路径,随机的进行赋值,然后找到一条路径(不一定非得到达叶结点中间也可能结束掉),然后随机的找出路径来进行采样,然后看一看它们的概率是多少,根据这个概率来算期望值,这是一种搜索树结点数量的一种方法。
1、 从根开始,随机选择一条路经
直到不能分支为止,
即 从 x 1 , x 2 , … , 依 次 对 x i 赋 值 , 每 个 x i 的 值 是 从 当 时 的 S i 中 随 机 选 取 , 直 到 向 量 不 能 扩 张 为 止 . 即从x_1, x_2 , …, 依次 对x_i赋值,每个x_i 的值是从当时的S_i 中随机选取,直到向量不能扩张为止. 即从x1,x2,…,依次对xi赋值,每个xi的值是从当时的Si中随机选取,直到向量不能扩张为止.
2、假定搜索树的其他 ∣ S i ∣ − 1 | S_i | −1 ∣Si∣−1个分支与以上随机选出的路径一样,计数搜索树的点数.
3、 重复步骤1 和2,将结点数进行概率平均
二、伪码
输入:n 为皇后数,t 为抽样次数
输出:sum, 即t 次抽样路长平均值
1. sum←0
2.for i←1 to t do // 取样次数t
3. m←Estimate(n)// m为结点数
4. sum ←sum + m
5. sum ←sum / t
三、4后搜索树遍历的结点
1、随机选择路径1
随机寻找的过程,也就是解有一个向量,向量的构成
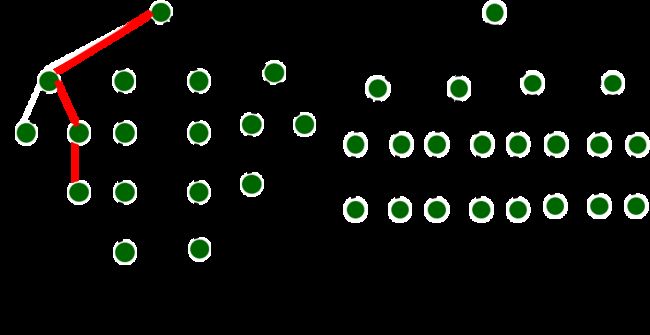
比如找到一条路径(虽随机选择的路径),随机赋值来选择的路径选出来,路径长度是<1,4,2>,估计所有的可能性,这条路径在这个树里面:第一个结点有4种选择;第二个结点有2种选择;第三个结点有1种选择。
有8条路径是可以重复的,用结点进行复制,认为所有的结点都是这么长,用随机选择的一条路径是所有路径的拷贝,所有路径都是它的一种复制,用它来估计一下是21。
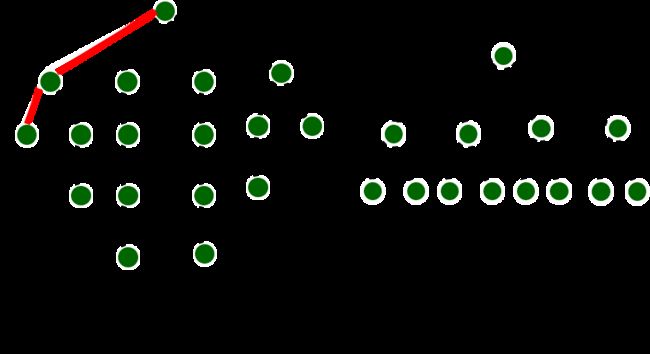
2、随机选择路径2
如果我们再随机选择一条路径,认为其他的路径都是按照这种方法走下来的,都是这样的一种选择,这个时候就相当于结点数估计出来有17个。
这条路径它中间没有任何的分支,把它复制一下,就有4条,也就是说它在第一个结点发现有4个分支(第一种选择有4种),所以就把它复制4次,把所有的结点数,这个地方就有4x4+1个结点,我们认为随机找一条给它复制。
当然复制的时候,要考虑它的分支的个数,比如说路径2往下面走的结点没有别的任何分支,只有第一个结点处有4种选择,所以说给它复制4次。
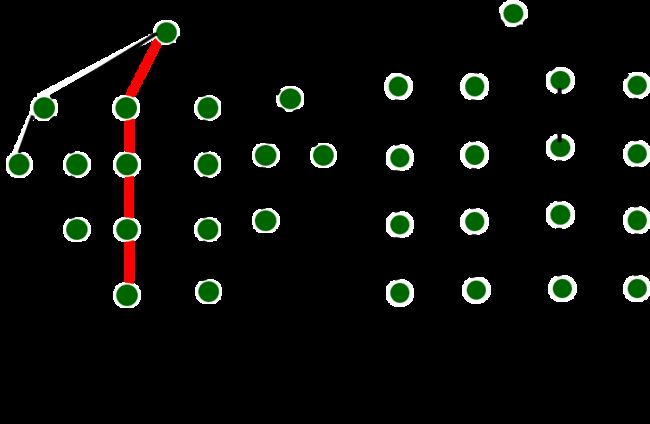
3、随机选择路径3
随机赋值选出来的路径,第一个分支有4种选择,第二个分支的时候有两种选择。
所以第一个路径这个点单独抽出来复制4次,然后第二个路径这个点,有两种选择,给它复制2次,认为随机找一条代替所有,复制完成后把结点数算出来,接下来再随机选,当选择次数越选越多的时候,这个时候就可以来抽样。
4、估计结果
假设4 次抽样测试:
case1: 1次,
case2: 1次,
case3: 2次,
平均结点数=(21×1+17×1+13×2)/4=16
搜索空间访问的结点数为17
每次假如选择的一条路径,对这条路径做完整的复制以后,把它的结点数作为搜索空间结点数的一个估计,采样了多次,根据大数定律去估计平均值和期望值是多少。
最后估计出来发现是16,但实际上是17,这个值就可以做成它的一个很好的估计值,这个就是搜索树里面的蒙特卡洛方法。
四、实例
抽样的时候要注意,在复制的时候有一个分支,在搜索树的分支里面,选出和它路径一样的随机树,一样的点。
1、一次抽样
m为本次取样得到的树结点总数
k 为层数
r 2 为 上 层 结 点 数 r_2 为上层结点数 r2为上层结点数
r 1 为 本 层 结 点 数 r_1为本层结点数 r1为本层结点数
r 1 = r 2 ⋅ 分 支 数 r_1= r_2⋅分支数 r1=r2⋅分支数
n 为树的层数
从树根向下计算,随机选择,直到树叶.
r 2 = 2 r_2 =2 r2=2
r 1 = r 2 ⋅ 3 = 6 r_1= r_2⋅3 =6 r1=r2⋅3=6

2、子过程的伪码
算法Estimate(n)
1. m←1; r2←1; k←1// m 为结点总数
2. while k≤ndo
3. if Sk=∅then return m
4. r1←|Sk|*r2 // r1为扩张后结点总数
5. m←m+r1 // r2为扩张前结点总数
6. xk←随机选择Sk的元素
7. r2←r1
8. k←k+1
五、总结
Monte Carlo 方法
1、目的:估计搜索树真正访问结点数
2、步骤: 随机抽样,选择一条路径
用这条路径代替其他路径
逐层累加树的结点数
多次选择,取结点数的平均值