武器系统仿真技术(二):末端制导系统蒙特卡洛仿真法

1.蒙特卡洛仿真方法的统计特性

假设一个$m$个系统输出数据$\{y_i{\}}_{i=1}^m$，$N$次循环得到$N$组数据$\{\{y_i{\}}_{i=1}^m{\}}_{j=1}^N$。那么实际上会有以下两组统计特性指标:

1.2数值统计特性:

(1)数学期望:$E(y)\approx \frac{1}{N}{\sum }_{k=1}^N{y}_k$

(2)方差:${\sigma }_y^2\approx \frac{1}{N}{\sum }_{K=1}^N{(y_k-Ey)}^2$

(3)概率密度函数:$p(y)\approx \frac{N_y}{N\Delta y}$,其中若将区间$(a,b)$划分为$L$段,则$\Delta y=\frac{b-a}{L}$,其中$N_y$是数值满足不等式:

$(y-0.5\Delta y)<y<(y+0.5\Delta y)$的个数,用曲线拟合可以得到概率密度函数$p(y)$

1.3 时间统计特性计算(Y(t)是平稳随机过程):

(1)时间均值$E\{y_K(t)\}=li{m}_{T\to \infty }\frac{1}{T}{\int }_0^T{y}_K(t)dt$

(2)时间均方差${\sigma }_{y_K}^2=li{m}_{T\to \infty }\frac{1}{T}{\int }_0^T\{y_K(t)-E\{y_K(t)\}{\}}^{2}dt$

(3)自相关函数$R_{y_K}(t_1,t_2)=li{m}_{T\to \infty }\frac{1}{T}{\int }_0^T{y}_K(t)y_K(t+\tau )dt$

2.仿真实例

以导弹末端制导系统仿真为例,说明该仿真方法的应用

2.1仿真原理及算法

1.系统组成

一个导弹末端制导系统由控制系统,导引头,目标运动,导弹运动和相对运动等若干环节组成,这些环节构成了末端制导系统(如下图所示)。符号说明:$R:$视线距,$\lambda :$视线角,$a_c$:控制指令,$a_L$:导弹控制系统对制导指令的响应(实际视线法向加速度)。采用比例制导法,那么$a_c=K{v}_c\dot{\lambda }$,其中$K$为比例导引系数,$v_c$为导弹实际接近目标的速度,$\dot{\lambda }$为目标的实际角速度。

2.工作原理

由视线角速度$\dot{\lambda }$进过制导计算机形成制导指令,导弹控制系统执行制导指令,改变导弹的姿态运动并且给出导弹视线法向加速度,影响导弹同目标运动的相对运动,使得$R(t_F)$(即在一段飞行时间内导弹的视线距尽可能小)。

仿真目的在于通过仿真活得脱靶量$y(t_F)$在不同的$m$个飞行时间内由于随机目标机动运动造成的均方根${\sigma }_{y(1)},{\sigma }_{y(2)},{\sigma }_{y(3)}...,{\sigma }_{y(m)}$,以及相关的数值和时间统计特性。

3.制导系统的线性化模型

仿真过程中:$a_T$是目标的运动加速度是随机量,其代表的是一类“电报机动”的随机干扰模型,即目标要么正的最大加速度机动,要么负的最大加速度机动,机动开始时间和正负方向都是随机的。当运动规律确定的时候,开始时间随机的随机扰动可以描述为:
$$\begin{gathered} x(t)=h(t-T) \\ {p}_T(t)=\frac{1}{t_F}(0\le t\le t_F),0(else) \end{gathered}$$
在本例中,目标做随机机动,其视线法向加速度 $a_T$的幅值为29.4m/s,加速度的正负符号和开始时间$T$为在区间$(0,t_F)$内的等概率的随机量。其描述如下:
$$\begin{gathered} a_T(t)=C_{oef}\ast a_T\ast sign(t-T) \\ {C}_{oef}=1(Random>0.5),-1(random<0.5),p_T(t)=\frac{1}{t_F}(0\le t\le t_F),0(else) \end{gathered}$$
其中$R(0)$为视线距初值,$t_F=\frac{R(0)}{v_c}$,$y(t_F)$定义为脱靶量,$t_{go}=t_F-t$为剩余飞行时间,$v_c{t}_{go}$为剩余飞行距离,视线角为$\lambda =\frac{y}{v_c{t}_{go}}$。一些其他的参数标注为v_c=1219m/s,K=3,系统时间常数T=1s,导弹速度v_m=914.4m/s。

设$X=(y,\dot{y},a_c,a_L{)}^T$系统的状态方程可以描述为:
$$\dot{X}=f(t,X,a_T,t_F)$$
其中:$\dot{X}=(X(2),a_T-X(4),K(\frac{X(2)}{t_F-t}+\frac{X(1)}{(t_F-t{)}^2}),\frac{X(3)-X(4)}{T}{)}^T$。

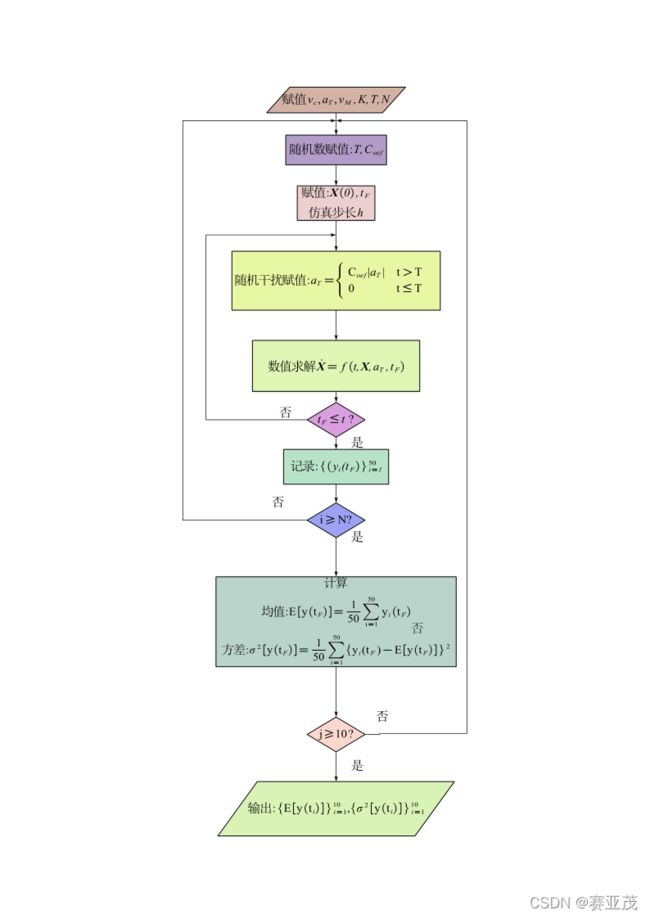
其流程图可以表述如下:

2.2 仿真代码及结果

clc,clear;close all;
v_c = 1219;K = 3;T = 1;
v_m = 914.4;a_T = 29.4;
coffient.K = K;
coffient.a_T = a_T;
t_f = 10;h = 0.1;
%重要参数区间
E = [];D = [];time_point = [];
for time = h:h:t_f
    T =  time*rand;%产生常数T
    x0 = [0 0 0 0]';
    %下面进行参数结构体赋值
    coffient.t_F = time;
    coffient.T = T;
    [tout,yout] = Adams_4v(@(t,x)missle_model(t,x,coffient),[0 time],x0,(time - 0)/50);
    %下面计算具体参数
    time_point = [time_point;time];
    E = [E;mean(yout(:,1))];
    D = [D;sqrt(mean((yout(:,1) - mean(yout(:,1))).^2))];
end
%下面进行绘图操作
subplot(121)
hold on;box on;grid on;
plot(time_point,E,'bo');
xlabel('t_F/s');ylabel('E(y_P{t_F})/m');
title('数学期望仿真结果');
subplot(122)
hold on;box on;grid on;
plot(time_point,D,'r-+');
xlabel('t_F/s');ylabel('\sigma(y_P{t_F})/m');
title('方差仿真结果');

%导弹末端制导模型
function f = missle_model(t,x,coffient)
    K = coffient.K;
    t_F = coffient.t_F;
    aT = coffient.a_T;
    T = coffient.T;
    f = zeros(4,1);
    %下面给出随机a_T
    if rand >= 0.5
        C_oef = 1;
    else
        C_oef = -1;
    end
    if t>T
        flag = 1;
    else
        flag = 0;
    end
    a_T = C_oef*aT*flag;
    %下面是函数导数
    f(1) = x(2);
    f(2) = a_T - x(4);
    f(3) = K*(x(2)/(t_F - t) + x(1)/(t_F - t)^2);
    f(4) = (x(3) - x(4))/T;
end

%下面是4阶亚当姆斯预估-校正法
function [t_,y] = Adams_4v(f,tspan,x0,h)
    t_min = tspan(1);t_max = tspan(2);
    t_f1 = [t_min,t_min+h,t_min+2*h,t_min+3*h];
    t_f2 = [t_min+h,t_min+2*h,t_min+3*h,t_min+4*h];
    fn1 = zeros(1,4);fn2 = zeros(1,4);
    y = [];t_ = [];x = x0;t = t_min;
    %下面是用RK-4初始化提供初值
    while(t<t_f1(end))
        y = [y;x'];
        t_ = [t_;t];
        K1 = h*f(t,x);
        K2 = h*f(t + h/2,x + 1/2*K1);
        K3 = h*f(t + h/2,x + 1/2*K2);
        K4 = h*f(t + h,x + K3);
        x = x + (K1 + 2*K2 + 2*K3 + K4)/6;
        t = t + h;
    end
    for t = (t_min+3*h):h:t_max
        y = [y;x'];t_ = [t_;t];
        x_ = x + h/24*(55*f(t,x)-59*f(t-h,x)+37*f(t-2*h,x)-9*f(t-3*h,x));
        f_ = f(t+h,x_);
        x = x + h/24*(9*f_ + 19*f(t,x) - 5*f(t-h,x) + f(t-2*h,x));
    end
end

结果: