关于Python的ARCH包（五）

1.4 预测示例

1.4.1 数据

1.4.2 基本预测

1.4.3 替代预测方案

1.4.4 TARCH

××××××××××××××××××××××

1.4.1 Data

这些示例是用来Yahoo网站的标准普尔500指数，并通过pandas-datareader包管理数据下载。

import datetime as dt
import sys

import numpy as np
import pandas as pd
import pandas_datareader.data as web

from arch import arch_model

start = dt.datetime(2000,1,1)
end = dt.datetime(2017,1,1)
data = web.get_data_famafrench('F-F_Research_Data_Factors_daily', start=start, end=end)
mkt_returns = data[0]['Mkt-RF'] +  data[0]['RF']
returns = mkt_returns

 

1.4.2 基本预测

预测可以使用标准GARCH（p,q）模型及以下三种方法的任一种生成：

• 解析法
• 基于模拟法
• 基于自举法

默认预测将用完样本中的最后一个观察值，对样本外的数据进行预测。

预测开始时，将使用给定的模型和估计所得到的参数。

am = arch_model(returns, vol='Garch', p=1, o=0, q=1, dist='Normal')
res = am.fit(update_freq=5)

Iteration:      5,   Func. Count:     39,   Neg. LLF: 6130.463290920333
Iteration:     10,   Func. Count:     71,   Neg. LLF: 6128.4731771407005
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 6128.4731681952535
            Iterations: 11
            Function evaluations: 77
            Gradient evaluations: 11

forecasts = res.forecast()

预测被放在 ARCHModelForecast目标类中，其具有四个属性：

• mean - 预测均值
• residual_variance - 预测残差的方差，即 。
• variance - 预测过程的方差，即 . 当模型均值动态变化时，比如是一个AR过程时，该方差不同于残差方差。
• simulations - 一个包括模拟详细信息的对象类，仅仅在预测方法设为模拟或自举时可用；如果使用解析方法analytical，则该选项不可用。

这三种结果均返回h.#列的DataFrame格式数据， # 表示预测步数。也就是说，h.1 对应于提前一步预测，而h.10对应于提前10步预测。

默认预测仅仅产生1步预测。

print(forecasts.mean.iloc[-3:])
print(forecasts.residual_variance.iloc[-3:])
print(forecasts.variance.iloc[-3:])

                h.1
Date                
2016-12-28       NaN
2016-12-29       NaN
2016-12-30  0.061286
                 h.1
Date                
2016-12-28       NaN
2016-12-29       NaN
2016-12-30  0.400956
                 h.1
Date                
2016-12-28       NaN
2016-12-29       NaN
2016-12-30  0.400956

更长步数的预测可以通过传递horizon参数进行计算得出。

forecasts = res.forecast(horizon=5)
print(forecasts.residual_variance.iloc[-3:])

                 h.1       h.2       h.3       h.4       h.5
Date                                                        
2016-12-28       NaN       NaN       NaN       NaN       NaN
2016-12-29       NaN       NaN       NaN       NaN       NaN
2016-12-30  0.400956  0.416563  0.431896  0.446961  0.461762

没有计算的值则用 nan 填充。

1.4.3 替代预测方案

1.4.3.1 固定窗口预测

固定窗口预测使用截至给定日期的数据来产生此日期后的全部预测结果。在初始化模型时，可以通过传递进全部数据，在使用fit.forecast()时使用last_obs将会产生该日期后的全部预测结果。

注意： last_obs 遵从Python序列规则，因此last_obs中的实际日期并非在样本中。

res = am.fit(last_obs = '2011-1-1', update_freq=5)
forecasts = res.forecast(horizon=5)
print(forecasts.variance.dropna().head())

Iteration:      5,   Func. Count:     38,   Neg. LLF: 4204.91956121224
Iteration:     10,   Func. Count:     72,   Neg. LLF: 4202.815024845146
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 4202.812110685669
            Iterations: 12
            Function evaluations: 84
            Gradient evaluations: 12
                 h.1       h.2       h.3       h.4       h.5
Date                                                        
2010-12-31  0.365727  0.376462  0.387106  0.397660  0.408124
2011-01-03  0.451526  0.461532  0.471453  0.481290  0.491043
2011-01-04  0.432131  0.442302  0.452387  0.462386  0.472300
2011-01-05  0.430051  0.440239  0.450341  0.460358  0.470289
2011-01-06  0.407841  0.418219  0.428508  0.438710  0.448825

1.4.3.2 滚动窗口预测

滚动窗口预测使用固定长度样本，且随即产生基于最后一个观察值的一步式预测。这个可以通过first_obs和last_obs来实现。

index = returns.index
start_loc = 0
end_loc = np.where(index >= '2010-1-1')[0].min()
forecasts = {}
for i in range(20):
    sys.stdout.write('.')
    sys.stdout.flush()
    res = am.fit(first_obs=i, last_obs=i+end_loc, disp='off')
    temp = res.forecast(horizon=3).variance
    fcast = temp.iloc[i+end_loc-1]
    forecasts[fcast.name] = fcast
print()
print(pd.DataFrame(forecasts).T)

                 h.1       h.2       h.3
2009-12-31  0.598199  0.605960  0.613661
2010-01-04  0.771974  0.778431  0.784837
2010-01-05  0.724185  0.731008  0.737781
2010-01-06  0.674237  0.681423  0.688555
2010-01-07  0.637534  0.644995  0.652399
2010-01-08  0.601684  0.609451  0.617161
2010-01-11  0.562393  0.570450  0.578447
2010-01-12  0.613401  0.621098  0.628738
2010-01-13  0.623059  0.630676  0.638236
2010-01-14  0.584403  0.592291  0.600119
2010-01-15  0.654097  0.661483  0.668813
2010-01-19  0.725471  0.732355  0.739187
2010-01-20  0.758532  0.765176  0.771770
2010-01-21  0.958742  0.964005  0.969229
2010-01-22  1.272999  1.276121  1.279220
2010-01-25  1.182257  1.186084  1.189883
2010-01-26  1.110357  1.114637  1.118885
2010-01-27  1.044077  1.048777  1.053442
2010-01-28  1.085489  1.089873  1.094223
2010-01-29  1.088349  1.092875  1.097367

2.3.3 递归预测方案

除了初始数据维持不变意外，其他方面递归方法与滚动方法类似. 这个可以方便地通过略掉first_obs选项而实现。

import pandas as pd
import numpy as np
index = returns.index
start_loc = 0
end_loc = np.where(index >= '2010-1-1')[0].min()
forecasts = {}
for i in range(20):
    sys.stdout.write('.')
    sys.stdout.flush()
    res = am.fit(last_obs=i+end_loc, disp='off')
    temp = res.forecast(horizon=3).variance
    fcast = temp.iloc[i+end_loc-1]
    forecasts[fcast.name] = fcast
print()
print(pd.DataFrame(forecasts).T)

 h.1       h.2       h.3
2009-12-31  0.598199  0.605960  0.613661
2010-01-04  0.772200  0.778629  0.785009
2010-01-05  0.723347  0.730126  0.736853
2010-01-06  0.673796  0.680934  0.688017
2010-01-07  0.637555  0.644959  0.652306
2010-01-08  0.600834  0.608511  0.616129
2010-01-11  0.561436  0.569411  0.577324
2010-01-12  0.612214  0.619798  0.627322
2010-01-13  0.622095  0.629604  0.637055
2010-01-14  0.583425  0.591215  0.598945
2010-01-15  0.652960  0.660231  0.667447
2010-01-19  0.724212  0.730968  0.737673
2010-01-20  0.757280  0.763797  0.770264
2010-01-21  0.956394  0.961508  0.966583
2010-01-22  1.268445  1.271402  1.274337
2010-01-25  1.177405  1.180991  1.184549
2010-01-26  1.106326  1.110404  1.114450
2010-01-27  1.040930  1.045462  1.049959
2010-01-28  1.082130  1.086370  1.090577
2010-01-29  1.082251  1.086487  1.090690

1.4.4 TARCH模型

1.4.4.1 解析预测

所有的 ARCH-类模型都可以进行一步解析预测。更长步数的解析预测仅针对特定模型的特别设定而言。TARCH模型下当步数大于1时，不存在解析式预测（封闭式预测） 。因此，更长步数的解析需要采用模拟或自举方法。尝试使用解析方法mothod='analytical'去产生大于1步的预测结果，则会返回ValueError错误值。

# TARCH specification
am = arch_model(returns, vol='GARCH', power=2.0, p=1, o=1, q=1)
res = am.fit(update_freq=5)
forecasts = res.forecast()
print(forecasts.variance.iloc[-1])

Iteration:      5,   Func. Count:     44,   Neg. LLF: 6037.930348422024
Iteration:     10,   Func. Count:     82,   Neg. LLF: 6034.462051044527
Optimization terminated successfully.    (Exit mode 0)
            Current function value: 6034.461795464493
            Iterations: 12
            Function evaluations: 96
            Gradient evaluations: 12
h.1    0.449483
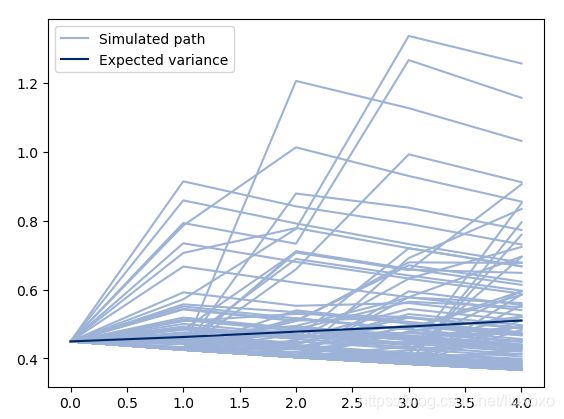
Name: 2016-12-30 00:00:00, dtype: float64

1.4.4.2 模拟预测

当使用模拟或自举方法进行预测时，关于ARCHModelForecast对象的一种属性非常有价值– simulation.

import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,1)
subplot = (res.conditional_volatility['2016'] ** 2.0).plot(ax=ax, title='Conditional Variance')

forecasts = res.forecast(horizon=5, method='simulation')
sims = forecasts.simulations

lines = plt.plot(sims.residual_variances[-1,::10].T, color='#9cb2d6')
lines[0].set_label('Simulated path')
line = plt.plot(forecasts.variance.iloc[-1].values, color='#002868')
line[0].set_label('Expected variance')
legend = plt.legend()

import seaborn as sns
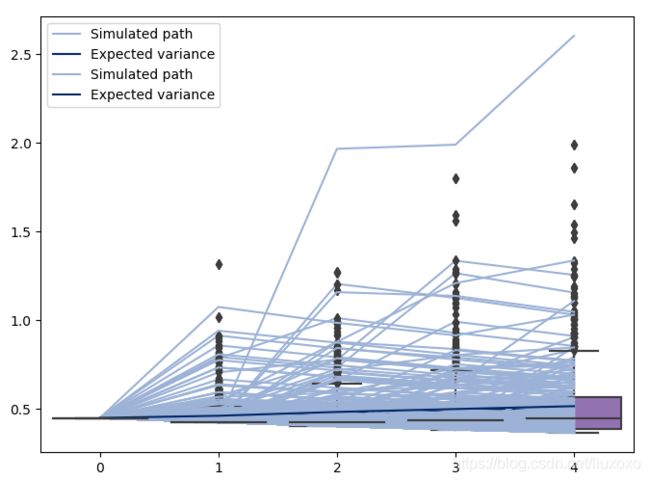
sns.boxplot(data=sims.variances[-1])

1.4.4.3 自举预测

除了基于历史数据而非基于假定分布以外，自举预测方法几乎与模拟预测一致。使用这种方法的预测也返回一个ARCHModelForecastSimulation对象类，包括关于模拟路径的信息。

forecasts = res.forecast(horizon=5, method='bootstrap')
sims = forecasts.simulations

lines = plt.plot(sims.residual_variances[-1,::10].T, color='#9cb2d6')
lines[0].set_label('Simulated path')
line = plt.plot(forecasts.variance.iloc[-1].values, color='#002868')
line[0].set_label('Expected variance')
legend = plt.legend()