梯度下降算法——theta参数更新公式的数学理解

（notice：粗体以示向量）

一、引出算法

在学习 Linear Regression 算法时，经典案例就是房价预测。在通过一系列预处理操作后，得到一个带有特征变量$x$和可学习参数$\theta$的假设函数:
$$h_{\theta }(\text{x})={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$

一般式：

$$h_{\theta }(\text{x})=\sum _{i=0}^n{\theta }_i{x}_i={\mathbf{\theta }}^T\cdot \text{x}（n为特征数）$$
下一步要做的就是，构造一个均方损失函数：

$$J(\mathbf{\theta })=\frac{1}{2}\sum _{k=1}^m(h_{\theta }({\text{x}}^k)-y^k{)}^2（m为训练集样本数量）$$

$$h_{\theta }({\text{x}}^k)-y^k$$
表示第 k 个样本的实际预测值和其真实值的差异，即“训练误差”。所有样本的训练误差之和为损失函数$J(\mathbf{\theta })$ 。 $J(\mathbf{\theta })$ 越小，则说明可学习参数$\mathbf{\theta }$调整的越好，算法泛化能力有可能也越好。

想让损失函数$J(\mathbf{\theta })$ 变小，就只能迭代优化可学习参数$\mathbf{\theta }$

而想要优化参数$\mathbf{\theta }$，就可以使用梯度下降算法

---

二、梯度下降算法直观理解

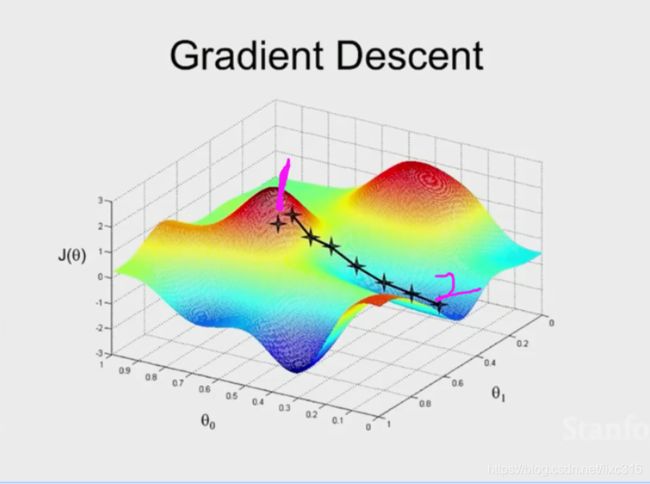
直观看，假如损失函数的起始位置在上图 “1”的位置。由坐标轴刻度可知，此时的损失函数$J(\mathbf{\theta })$的位置很高，数值很大。需要调整可学习参数$\mathbf{\theta }$以减小在训练集上$J(\mathbf{\theta })$的数值。
如图所示，损失函数$J(\mathbf{\theta })$不断的寻找比当前位置更低的地方作为下一步驻留地，最后在位置“2”处停止寻找。此时便得到一个局部最优解$\mathbf{\theta }$.

这使用的就是下面这个更新公式：
$${\theta }_i:={\theta }_i-\alpha \frac{\partial }{\partial {\theta }_i}J(\mathbf{\theta })$$
其中：(注意区分粗体)
$$\frac{\partial }{\partial {\theta }_i}J(\mathbf{\theta })=\frac{\partial }{\partial {\theta }_i}\frac{1}{2}\sum _{k=1}^m(h_{\theta }({\text{x}}^k)-y^k{)}^2$$

$$=\frac{\partial }{\partial {\theta }_i}\frac{1}{2}\sum _{k=1}^m({\mathbf{\theta }}^T\cdot {\text{x}}^k-y^k{)}^2$$

$$=\sum _{k=1}^m({\mathbf{\theta }}^T\cdot {\text{x}}^k-y^k)\cdot x_i$$

$$=\sum _{k=1}^m(h_{\theta }({\text{x}}^k)-y^k)\cdot x_i$$
经推导得到可学习参数$\theta$的更新公式：
$${\theta }_i:={\theta }_i+\alpha \cdot \sum _{k=1}^m(y^k-h_{\theta }({\text{x}}^k))\cdot x_i^k$$
公式意思是：使用第k个样本点的数据更新$\mathbf{\theta }$中的第i个${\theta }_i$分量

---

三、疑惑

直观理解很容易，不理解的是：


为什么通过${\theta }_i:={\theta }_i+\alpha \cdot {\sum }_{k=1}^m(y^k-h_{\theta }({\text{x}}^k))\cdot x_i^k$调整$\mathbf{\theta }$，就可以把损失函数$J(\mathbf{\theta })$尽可能的减小?

换言之，以cs229课程截图为例，为什么这个公式能使损失函数$J(\mathbf{\theta })$ 步步走到更低点，迭代次数完成后到达一个局部最低点？

由此产生两个问题：

1、损失函数下降方向是怎么选择的？

2、$\mathbf{\theta }$的更新公式为什么是这个形态？

---

四、证明

问题1：损失函数下降方向是怎么选择的？

证明：

梯度的概念，如下图：

（“梯度”是“梯度向量”的简称，“梯度”和“方向导数”是有本质区别和联系的）

简言之：

梯度是一个向量，其分量是由函数偏导数构成的。

梯度方向是一个函数上升最快的方向

负梯度方向是一个函数下降最快的方向

===》由此得：Gradient Descent算法选择损失函数下降方向时，是选择负梯度方向

问题2：$\mathbf{\theta }$的更新公式为什么是这个形态？

证明：

(1)高等数学中有一个知识点: 泰勒公式

若函数$f(x)$在$x_0$处可导，则在$x_0$的领域$U(x_0)$内有：
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+O(x-x_0)$$
也即：
$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)$$

(2)同理可得$J(\mathbf{\theta })$在${\mathbf{\theta }}_0$某领域内的泰勒展开式
$$J(\mathbf{\theta })=\frac{1}{2}\sum _{k=1}^m(h_{\theta }({\text{x}}^k)-y^k{)}^2$$

$$J(\mathbf{\theta })=J({\mathbf{\theta }}_0)+J^{\prime }({\mathbf{\theta }}_0)(\mathbf{\theta }-{\mathbf{\theta }}_0)$$

$\mathbf{\theta }$是向量，得求偏导数。现使用第k个样本点的数据更新第i个分量${\theta }_i$为例

$$J(\mathbf{\theta })-J({\mathbf{\theta }}_0)=\frac{\partial }{\partial {\theta }_i}\frac{1}{2}\sum _{k=1}^m({{\mathbf{\theta }}_0}^T\cdot {\text{x}}^k-y^k{)}^2(\mathbf{\theta }-{\mathbf{\theta }}_0)$$

$$=\sum _{k=1}^m({{\mathbf{\theta }}_0}^T\cdot {\text{x}}^k-y^k)\cdot x_i^k\cdot (\mathbf{\theta }-{\mathbf{\theta }}_0)$$

其中红色部分就是梯度（一元函数的导数可以看作梯度），将这部分拿出来取反，即负梯度方向

（3）参数更新公式：

以$f(x)$为例：

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)$$

$f(x)$在$x_0$处沿着负梯度方向下降，只需要更新$x$即可。

$$x=x_0+(-f^{\prime }(x_0)\cdot \alpha ),（\alpha 为学习率）$$

同理可得：

<1>现有负梯度方向：
$$-\frac{\partial }{\partial {\theta }_i}{J}^{\prime }(\mathbf{\theta })=-\sum _{k=1}^m({\mathbf{\theta }}^T\cdot {\text{x}}^k-y^k)\cdot x_i^k$$

<2>同理可得$J(\mathbf{\theta })$在${\mathbf{\theta }}_0$某领域内的泰勒展开式
$$J(\mathbf{\theta })=J({\mathbf{\theta }}_0)+J^{\prime }({\mathbf{\theta }}_0)(\mathbf{\theta }-{\mathbf{\theta }}_0)$$

$${\theta }_i:={\theta }_i+(-\alpha \cdot \sum _{k=1}^m({\mathbf{\theta }}^T\cdot {\text{x}}^k-y^k)\cdot x_i^k)$$

$${\theta }_i:={\theta }_i+\alpha \cdot \sum _{k=1}^m(y^k-{\mathbf{\theta }}^T\cdot {\text{x}}^k)\cdot x_i^k$$

${\theta }_i:={\theta }_i+\alpha \cdot {\sum }_{k=1}^m(y^k-h_{\theta }({\text{x}}^k))\cdot x_i^k$

${\theta }_i(i=0,1,\cdot \cdot \cdot \cdot n)$ 全部更新完后，$\mathbf{\theta }$整体更新完毕

===》以上便是 $\boldsymbol\theta$ 的更新公式形态的由来