梯度下降模拟点云表面的水流（路径规划）

问：在某块倾斜点云的表面有一颗水滴，收到引力的影响沿着点云表面滑动。求解此水滴应该流动到的最低点的轨迹。

梯度下降

梯度是描述在函数中某个位置的坡度（斜率），即对函数求导。在二维空间中的函数y =f（x）的梯度表现为位置x处的斜率（dy/dx），而在三维空间中的函数z = f（x，y）的梯度表现为位置（x，y）处的坡度(dz/dx,dz/dy)。

可以看出，对于三维函数来说，在某个二维位置处的梯度是唯一的二维数组(dz/dx,dz/dy)，由于二维数组中每个值都是x，y相对于z轴位置的偏导。此梯度能够在曲面上指示两个方向，分别是z值相对于x，y增长最快的的方向，和下降最快的方向。

梯度下降算法即为依据函数梯度从三维函数上某处的点进行一步步迭代下降的过程。而梯度上升则相反

路径规划

虽然函数能够表现三维曲面，但对于复杂的三维点云来说，使用函数来计算梯度非常耗时，得不偿失，此时，需要转换一下一下思路。既然梯度下降的目的为沿着梯度指示z轴的最快下降方向进行下降。则可以将其理解为受到垂直向下（z轴负方向）的引力影响的水滴在点云表面滑动的过程。

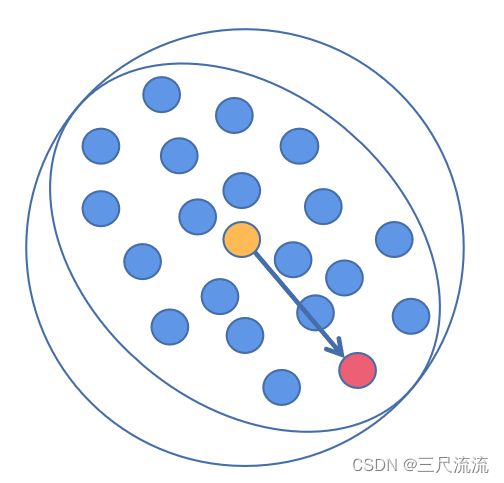
在三维点云中，梯度下降的方向即为此水滴位置（黄色点）到某个半径的球形范围内z轴最低点（红色点）的方向。红色点是水滴下一次移动到的位置。

 要模拟水流在点云表面的流动，需要描述出一条完整的路径，此时需要用到迭代的思想

参考“数据链表构成”

数据链表构成：Python与迭代函数的构造_三尺流流的博客-CSDN博客理解Python中迭代函数的构造思路https://blog.csdn.net/qq_55433334/article/details/127131917一文，依次将每次范围内的最低点作为下一次迭代的水滴位置，直到最终水滴范围内没有最低点为止。

逻辑流

1.导入一块有坡度的点云和原始水滴的位置。

2.设置下降步长最大的范围。

3.当水滴周围没有z轴更低的点时水滴停止流动，水滴到达终点。

完整代码

import numpy
import open3d as o3d
import matplotlib.pyplot as plt
import numpy as np

def drop_liter(pre_point, path_record, pcd, pcd_tree):
    pcdpts = np.asarray(pcd.points)

    # path_record.append(pre_point)
    for i in range(len(pcdpts)):
        if pcdpts[i][0] == pre_point[0] and pcdpts[i][1] == pre_point[1] and pcdpts[i][2] == pre_point[2]:
            [k1, idx1, _] = pcd_tree.search_radius_vector_3d(pcd.points[i], radius = 0.1)
            z_list =[]
            for i_idx in range(len(idx1)):
                z_list.append(numpy.asarray(pcd.points[idx1[i_idx]])[2])
            min_z = min(z_list)
            min_idx = z_list.index(min(z_list))
            if min_z < pre_point[2]:
                path_record.append(list(numpy.asarray(pcd.points[idx1[min_idx]])))
                pre_point = numpy.asarray(pcd.points[idx1[min_idx]])
                return drop_liter(pre_point, path_record, pcd, pcd_tree)
            else:
                return path_record

def path_view(path_record,pcd):
    x = np.asarray(pcd.points)[:,0]
    y = np.asarray(pcd.points)[:, 1]
    z = np.asarray(pcd.points)[:, 2]

    x_path = []
    y_path = []
    z_path = []
    for i in range(len(path_record)):
        x_path.append(path_record[i][0])
        y_path.append(path_record[i][1])
        z_path.append(path_record[i][2])


    fig1 = plt.figure()
    ax1 = fig1.add_subplot(111, projection='3d')
    ax1.set_xlabel("x")
    ax1.set_ylabel("y")
    ax1.set_zlabel("z")
    ax1.scatter(x, y, z, color='gray', marker='.')
    ax1.scatter(x_path, y_path, z_path, color='b', marker='o')
    plt.show()

    return None

if __name__ == '__main__':

    pcd = o3d.io.read_point_cloud("E:\db\1.pcd")
    pcd_tree = o3d.geometry.KDTreeFlann(pcd)
    #初始坐标
    pre_point = [3, 2, 1]
    path_record = []
    path_record.append(pre_point)
    path_record = drop_liter(pre_point, path_record, pcd, pcd_tree)
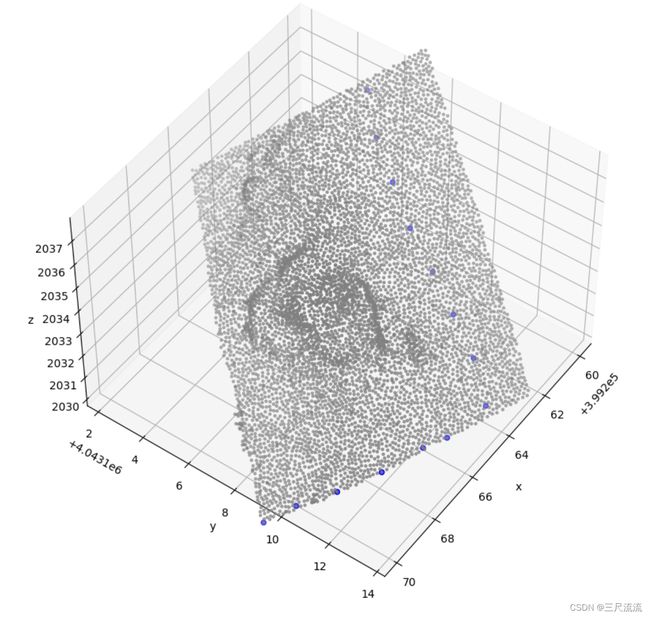
    path_view(path_record, pcd)

 图中我们分别以0.6，0.,8与1.2的速度进行滑动，通过分析我们得到：

1. 不同步长的水滴在同一点云表面滑动的路径其实并不相同，自动规划的路径形态会受到滑动速度的影响。

2. 应用梯度下降的想法进行路径规划并不一定能够到达表面点云的最低点，其动态位置很有可能受到表面凹凸性的影响到达点云某处的一个局部最低点即停止下降。

事实上这也确实符合现实中的规律，当窗户上的雨滴初速度较大时，其轨迹呈现为一条细长的直线，当其初速度就不大时，雨滴的轨迹就会被玻璃上的灰尘影响得歪歪扭扭。