机器学习-sklearn.datasets-load_iris数据集-回归算法和K近邻法(KNN)
学习机器学习一个月了,开始尝试做一些简单的练习
文章目录
- 1、 load_iris数据集
- 2、数据集处理
- 3、线性回归
-
- 3.1 回归训练
- 3.2 回归测试
- 3.3 对输入点进行判断
- 4、K近邻(KNN)算法
-
- 4.1 距离计算
- 4.2 计算准确率
- 4.3 k近邻法判断输入点类别
- 5、绘制函数图像
- 6、运行结果展示
- 7、完整代码
1、 load_iris数据集
Iris数据集在模式识别研究领域应该是最知名的数据集了,有很多文章都用到这个数据集。这个数据集里一共包括150行记录,其中前四列为花萼长度,花萼宽度,花瓣长度,花瓣宽度等4个用于识别鸢尾花的属性,第5列为鸢尾花的类别(包括Setosa,Versicolour,Virginica三类)。也即通过判定花萼长度,花萼宽度,花瓣长度,花瓣宽度的尺寸大小来识别鸢尾花的类别。
这里使用数据集的data、target两个属性进行机器学习的训练
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data
target= iris.target
print(data)
print(target)
这里data为训练所需的数据集,target为数据集对应的分类标签,属于监督学习
data数据集中的数据一共有4个属性,分别为
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
target为分类标签,与data中的数据相对应
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
data中的数据,前50个属于0类,中间50个属于1类,后50个属于2类
通过观察data数据集中的数据可知,在分类中四个属性,前两个属性的辨识度不是很高,后两个属性辨识度较高
这里因为是在做练习,所以只取数据集的前100个数据的前两个属性进行练习,当然取后两个属性也行,不过太简单了
2、数据集处理
首先是数据获取函数,没什么好说的,就是得到load_iris的数据并返回,代码如下:
# 数据获取
def get_data():
iris = load_iris()
data = iris.data
result = iris.target
return data, result
之后是对数据集的处理,将数据集分为训练集和测试集,这里数据比较少只有100条,分的时候应该尽可能随机,我的代码如下:
# 将数据处理为训练集和测试集
def data_deal(data, result):
data_list = []
for i in data:
tem_list = [i[0], i[1]]
data_list.append(tem_list)
res_list = []
for j in result:
res_list.append(j)
train_list = data_list[0: 10] + data_list[20: 80] + data_list[90: 100]
train_result = res_list[0: 10] + res_list[20: 80] + res_list[90: 100]
test_list = data_list[0: 40] + data_list[60: 100]
test_result = res_list[0: 40] + res_list[60: 100]
return data_list, train_list, test_list, train_result, test_result
这个分法并不好,提供一种思路:生成100以内随机数,将训练样本和训练结果对应的数据返回,选取80个作为训练集,将剩余的作为测试集
这里返回值为训练集、训练结果、测试集、测试集标准结果(用于与测试集最终结果比对计算准确率)
3、线性回归
3.1 回归训练
这里我用的方法并不是标准的线性回归方法,是自己的一个思路
下面是回归的训练方法,这里使用线性模型
y = w x + b y=wx+b y=wx+b
1、首先说明思路,先对训练集中的所有点x,y分别进行相加,除以个数,得到所有训练样本的几何中点
2、之后以这条线为回归模型上的一个定点,对回归模型进行旋转,设置初始w=0,b=0,即为水平线
3、通过学习率,对每次旋转的角度进行调整
4、在进行一次旋转时,若训练集中的样本的结果更加符合标准结果,那么继续向这个方向旋转,反之,若训练集结果与标准结果差的更远,那么则向反方向旋转
5、这里就涉及到一个斜率更新问题,斜率根据学习率进行更新,选定好的学习率也很重要
众所周知
斜 率 = t a n 夹 角 斜率=tan夹角 斜率=tan夹角
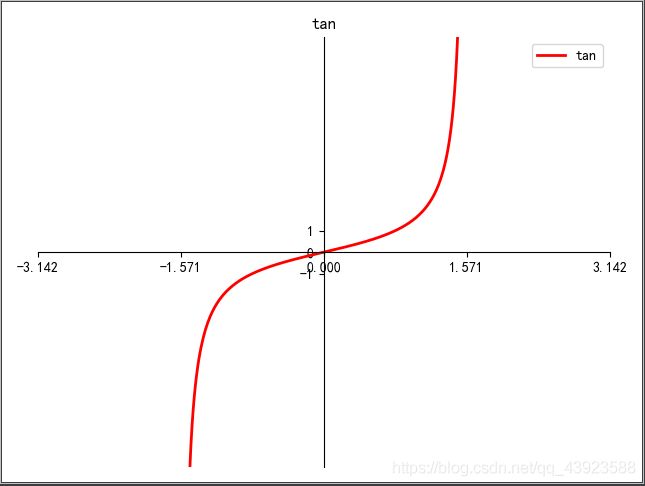
根据tan函数图像可知,初始时刻(w=0,b=0)的斜率为0
这时在tan的导数 较小>0 增长率较慢
所以在初始时刻时,要选取一个较大的学习率来对斜率进行更新,随着逐渐的更新,斜率的增长率开始变快,此时就需要一个较小的学习率来控制斜率了,因为此时斜率的变化对所拟合的直线会有较大的影响。
为此,初始的学习率给定为1,之后在每进行一次迭代,学习率乘0.9,这样可以使学习率较好的取适应拟合的直线,得到更高的准确率
乘0.9是通过测试得到的 ,迭代次数为1000此也是测试得到,而且继续增加迭代次数对模型的影响微乎其微,还会增加运行时间
# 回归方法训练
def train(learning_rate, iter_num, train_data, result):
x_c = 0
y_c = 0
for i in train_data:
x_c = x_c + i[0]
y_c = y_c + i[1]
m = x_c/len(train_data)
n = y_c/len(train_data)
w = 0
b = 0
ok_rate = 0
for i in range(iter_num):
train_r = []
b = n-w*m
count = 0
for j in train_data:
if j[1] > w*j[0]+b:
train_r.append(0)
else:
train_r.append(1)
for ii in range(len(result)):
if result[ii] == train_r[ii]:
count = count+1
train_ok_rate = count/len(train_data)
if ok_rate <= train_ok_rate:
w = w + learning_rate
else:
w = w - learning_rate
learning_rate = learning_rate*0.9
ok_rate = train_ok_rate
return ok_rate, w, b
3.2 回归测试
将回归得到的线性模型,用于对测试集中数据准确率的测试
将其测试结果与标准结果进行比对,得到测试准确率
# 回归方法测试
def test(w, b, test_list, test_result):
test_res = []
count = 0
for j in test_list:
if j[1] > w * j[0] + b:
test_res.append(0)
else:
test_res.append(1)
for i in range(len(test_result)):
if result[i] == test_res[i]:
count = count + 1
oks = count/len(test_result)
return oks
3.3 对输入点进行判断
判断输入点属于哪一类的一个方法,带入线性模型,判断其位于线上方还是下方
# 回归方法判断点的类型
def check_point(w, b, dot):
y = w*dot[0] + b
if y > dot[1]:
return "回归判断该点类别为0"
else:
return "回归判断该点类别为1"
4、K近邻(KNN)算法
4.1 距离计算
没什么好说的,就是简单的点到点的距离
# k近邻法计算距离方法
def distance(A, B):
return (abs((B[0]-A[0])**2+(B[1]-A[1])**2))**0.5
4.2 计算准确率
k近邻法思路为:给定一个点,选取与其距离最近的n个点,若这n个点中属于0类的点多,那么可以近似的认为该点也属于0类,否则将该点归为1类
在对所有点进行分类后,与标准结果进行比对,得出准确率
# k近邻法训练,测试准确率
def K_train(train_list, train_result, k):
dis_list = []
# 所有点到别的点的距离
for i in train_list:
dis = []
for j in train_list:
dis.append(distance(i, j))
dis_list.append(dis)
# 获取到训练集中每个点的最近5个点的索引
min_dis_list = []
for m in range(len(dis_list)):
temp = []
for n in range(int(k+1)):
temp.append(dis_list[m].index(min(dis_list[m])))
dis_list[m][dis_list[m].index(min(dis_list[m]))] = 100
temp.sort()
x = temp[1:]
min_dis_list.append(x)
# 根据索引判断对应点的类别
dot_type = []
for ii in min_dis_list:
mm = 0
nn = 0
for jj in ii:
if jj <= 50:
mm = mm+1
else:
nn = nn+1
if mm >= nn:
dot_type.append(0)
else:
dot_type.append(1)
# 计算准确率
count = 0
for xx in range(len(dot_type)):
if dot_type[xx] == train_result[xx]:
count = count+1
return count/len(dot_type)
4.3 k近邻法判断输入点类别
输入一个点,使用k近邻法判断其所属类别
# k近邻法判断点的类型
def K_check_point(dots, check_list, result):
dis = []
for i in check_list:
dis.append(distance(dots, i))
min_dis = []
for j in range(5):
min_dis.append(dis.index(min(dis)))
dis[dis.index(min(dis))] = 100
zero = 0
one = 0
for s in min_dis:
if result[s] == 0:
zero = zero+1
else:
one = one+1
if one > zero:
return "K近邻法判断该点类别为0"
else:
return "K近邻法判断该点类别为1"
5、绘制函数图像
使用matplotlib进行绘图,一张绘制所有点,另一张对训练集和测试集进行分别绘制
并将用户输入的点绘制到图像上
# 绘制函数图像和输入点
def fun_image(w, b, dot):
iris = load_iris()
irisFeature = iris.data
irisTarget = iris.target
ax1 = plt.subplot(1, 2, 1)
ax2 = plt.subplot(1, 2, 2)
plt.sca(ax1)
for i in range(0, 100):
if irisTarget[i] == 0:
type11 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="r")
elif irisTarget[i] == 1:
type22 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="g")
plt.title("show train and test")
plt.xlabel("ewidth")
plt.ylabel("elength")
x = np.linspace(4, 7, 256)
plt.plot(x, w * x + b, color='black')
plt.legend((type11, type22), ('0', '1'))
plt.plot(dot[0], dot[1], color='black', marker='+')
plt.sca(ax2)
for i in range(20, 80):
if irisTarget[i] == 0:
type1 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="r", marker="8")
elif irisTarget[i] == 1:
type2 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="g", marker="8")
for i in range(0, 20):
if irisTarget[i] == 0:
type3 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="blue", marker="v")
elif irisTarget[i] == 1:
plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="orange", marker="v")
for i in range(80, 100):
if irisTarget[i] == 0:
plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="blue", marker="v")
elif irisTarget[i] == 1:
type4 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="orange", marker="v")
plt.title("show all")
plt.xlabel("ewidth")
plt.ylabel("elength")
x = np.linspace(4, 7, 256)
plt.plot(x, w*x+b, color='black')
plt.plot(dot[0], dot[1], color='black', marker='+')
plt.legend((type1, type2, type3, type4), ('train-0', 'train-1', 'test-0', 'test-1'))
plt.show()
6、运行结果展示
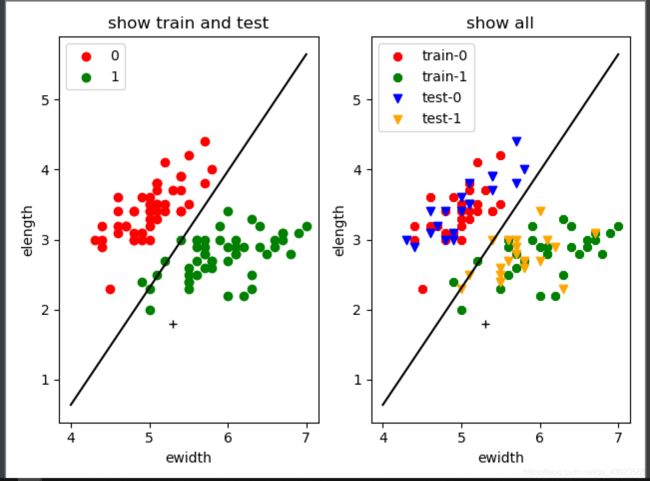
函数图像为:
其中包含 + 为手动输入的点
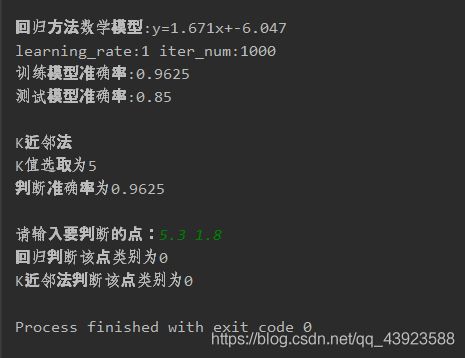
控制台输出的结果:
7、完整代码
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np
# 数据获取
def get_data():
iris = load_iris()
data = iris.data
result = iris.target
return data, result
# 将数据处理为训练集和测试集
def data_deal(data, result):
data_list = []
for i in data:
tem_list = [i[0], i[1]]
data_list.append(tem_list)
res_list = []
for j in result:
res_list.append(j)
train_list = data_list[0: 10] + data_list[20: 80] + data_list[90: 100]
train_result = res_list[0: 10] + res_list[20: 80] + res_list[90: 100]
test_list = data_list[0: 40] + data_list[60: 100]
test_result = res_list[0: 40] + res_list[60: 100]
return data_list, train_list, test_list, train_result, test_result
# 回归方法训练
def train(learning_rate, iter_num, train_data, result):
x_c = 0
y_c = 0
for i in train_data:
x_c = x_c + i[0]
y_c = y_c + i[1]
m = x_c/len(train_data)
n = y_c/len(train_data)
w = 0
b = 0
ok_rate = 0
for i in range(iter_num):
train_r = []
b = n-w*m
count = 0
for j in train_data:
if j[1] > w*j[0]+b:
train_r.append(0)
else:
train_r.append(1)
for ii in range(len(result)):
if result[ii] == train_r[ii]:
count = count+1
train_ok_rate = count/len(train_data)
if ok_rate <= train_ok_rate:
w = w + learning_rate
else:
w = w - learning_rate
learning_rate = learning_rate*0.9
ok_rate = train_ok_rate
return ok_rate, w, b
# 回归方法测试
def test(w, b, test_list, test_result):
test_res = []
count = 0
for j in test_list:
if j[1] > w * j[0] + b:
test_res.append(0)
else:
test_res.append(1)
for i in range(len(test_result)):
if result[i] == test_res[i]:
count = count + 1
oks = count/len(test_result)
return oks
# 绘制函数图像和输入点
def fun_image(w, b, dot):
iris = load_iris()
irisFeature = iris.data
irisTarget = iris.target
ax1 = plt.subplot(1, 2, 1)
ax2 = plt.subplot(1, 2, 2)
plt.sca(ax1)
for i in range(0, 100):
if irisTarget[i] == 0:
type11 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="r")
elif irisTarget[i] == 1:
type22 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="g")
plt.title("show train and test")
plt.xlabel("ewidth")
plt.ylabel("elength")
x = np.linspace(4, 7, 256)
plt.plot(x, w * x + b, color='black')
plt.legend((type11, type22), ('0', '1'))
plt.plot(dot[0], dot[1], color='black', marker='+')
plt.sca(ax2)
for i in range(20, 80):
if irisTarget[i] == 0:
type1 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="r", marker="8")
elif irisTarget[i] == 1:
type2 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="g", marker="8")
for i in range(0, 20):
if irisTarget[i] == 0:
type3 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="blue", marker="v")
elif irisTarget[i] == 1:
plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="orange", marker="v")
for i in range(80, 100):
if irisTarget[i] == 0:
plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="blue", marker="v")
elif irisTarget[i] == 1:
type4 = plt.scatter(irisFeature[i, 0], irisFeature[i, 1], c="orange", marker="v")
plt.title("show all")
plt.xlabel("ewidth")
plt.ylabel("elength")
x = np.linspace(4, 7, 256)
plt.plot(x, w*x+b, color='black')
plt.plot(dot[0], dot[1], color='black', marker='+')
plt.legend((type1, type2, type3, type4), ('train-0', 'train-1', 'test-0', 'test-1'))
plt.show()
# 回归方法判断点的类型
def check_point(w, b, dot):
y = w*dot[0] + b
if y > dot[1]:
return "回归判断该点类别为0"
else:
return "回归判断该点类别为1"
# k近邻法计算距离方法
def distance(A, B):
return (abs((B[0]-A[0])**2+(B[1]-A[1])**2))**0.5
# k近邻法训练,测试准确率
def K_train(train_list, train_result, k):
dis_list = []
# 所有点到别的点的距离
for i in train_list:
dis = []
for j in train_list:
dis.append(distance(i, j))
dis_list.append(dis)
# 获取到训练集中每个点的最近5个点的索引
min_dis_list = []
for m in range(len(dis_list)):
temp = []
for n in range(int(k+1)):
temp.append(dis_list[m].index(min(dis_list[m])))
dis_list[m][dis_list[m].index(min(dis_list[m]))] = 100
temp.sort()
x = temp[1:]
min_dis_list.append(x)
# 根据索引判断对应点的类别
dot_type = []
for ii in min_dis_list:
mm = 0
nn = 0
for jj in ii:
if jj <= 50:
mm = mm+1
else:
nn = nn+1
if mm >= nn:
dot_type.append(0)
else:
dot_type.append(1)
# 计算准确率
count = 0
for xx in range(len(dot_type)):
if dot_type[xx] == train_result[xx]:
count = count+1
return count/len(dot_type)
# k近邻法判断点的类型
def K_check_point(dots, check_list, result):
dis = []
for i in check_list:
dis.append(distance(dots, i))
min_dis = []
for j in range(5):
min_dis.append(dis.index(min(dis)))
dis[dis.index(min(dis))] = 100
zero = 0
one = 0
for s in min_dis:
if result[s] == 0:
zero = zero+1
else:
one = one+1
if one > zero:
return "K近邻法判断该点类别为0"
else:
return "K近邻法判断该点类别为1"
if __name__ == '__main__':
data, result = get_data()
data_list, train_list, test_list, train_result, test_result = data_deal(data, result)
learning_rate = 1
iter_num = 1000
ok_rate, w, b = train(learning_rate, iter_num, train_list, train_result)
test_ok_rate = test(w, b, test_list, test_result)
k = 5
K_ok_rate = K_train(train_list, train_result, k)
print("回归方法"
"数学模型:y={}x+{}\n"
"learning_rate:{}\titer_num:{}\n"
"训练模型准确率:{}\n"
"测试模型准确率:{}\n".format(round(w, 3), round(b, 3), learning_rate, iter_num, ok_rate, test_ok_rate))
print("K近邻法\n"
"K值选取为{}\n"
"判断准确率为{}\n".format(k, K_ok_rate))
dots = list(map(float, input("请输入要判断的点:").split()))
fun_image(w, b, dots)
print(check_point(w, b, dots))
print(K_check_point(dots, train_list, train_result))
耗时一晚上,终于做出来了,这是我做的第二个机器学习的练习,可能方法并不标准,代码写的也比较乱,太忙了,没有时间顾及这些了。
准研一暑假的自学,加油,自己!未来可期!