线性时变系统的PID控制-2

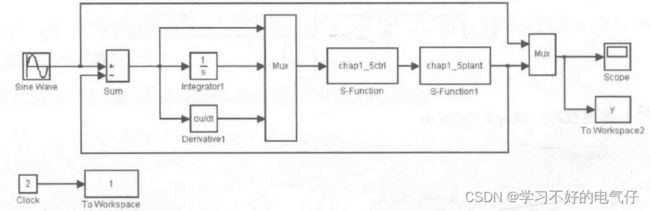
在线性时变系统的PID控制-1的基础上采用S函数进行Simulink仿真。

被控对象的描述方式可变换为：

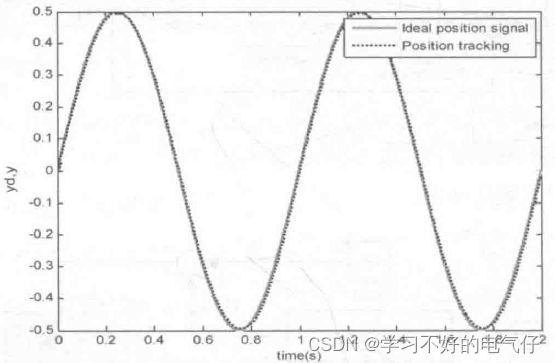
在S函数中，采用初始化、微分函数和输出函数，即mdllnitializeSizes函数、mdIDerivatives函数和mdlOutputs函数。在初始化中采用sizes结构，选择1个输出。3个输入，3个输入实现了P、I、D三项的输入。S函数嵌入在Simulink程序中。系统初始状态为: x(0)=0，t(0)=0。取kp=10，ki =2，kd=1，仿真结果如图所示。

仿真图：

S函数控制器子函数程序：chap1_5ctrl.m

function [sys,x0,str,ts]= spacemodel(t,x.u,flag)

switch flag,

case 0,

[sys,x0,str,ts]-mdlInitializeSizes;

case 1,

sys=mdlDerivatives(t,x,u);

case 3,

sys=mdlOutputs(t,x,u);

case {2,4,9}

sys=[ ];

otherwise

error(['Unhandled flag = ',num2st(flag)]);

end

function[sys,x0,str,ts]=mdlInitializeSizes

sizes = simsizes;

sizes.NumContStates=0;

sizes.NumDiscStates= 0;

sizes.NumOutputs=l;

sizes.NumInputs =3;

sizes.DirFeedthrough=l;

sizes.NumSampleTimes =1;% At least one sample time is needed

sys - simsizes(sizes);

x0=[];

str=[];

ts=[0 0];

function sys=mdlOutputs(t,x,u)

kp=10;

ki=2;

kd=1;

ut=kp*u(1)+ki*u(2)+kd*u(3);

sys(1)=ut;

S函数被控对象子程序：chap1_5plant.m

function [sys,x0,str,ts] = spacemodel(t,x,u, flag)

switch flag,

case 0,

[sys,x0,str,ts]=mdllnitializeSizes;

case 1,

sys=mdlDerivatives(t.x,u);

case 3,

sys=mdIOutputs(t,x,u);

case {2,4,9}

sys=[];

otherwise

error(['Unhandled flag =' num2str(flag));

end

function [sys,x0,str,ts]=mdllnitializeSizes

sizes= simsizes;

sizes.NumContStates= 2;

sizes.NumDiscStates=0;

sizes.NumOutputs=1;

sizes.NumInputs=1;

sizes.DirFeedthrough=0;

sizes.NumSampleTimes = l; % At least one sample time is needed

sys = simsizes(sizes);

x0=[0;0];

str=[];ts =[0 0];

function sys=mdlDerivatives(t,x,u) %Time-varying model

ut= u(1);

J=20+10*sin(6*pi*t);

K=400+300*sin(2*pi*t);sys( 1)-x(2);

sys(2)=-J*x(2)+K*ut;

function sys=mdlOutputs(t,x,u)

sys(1)=x(1);

作图程序：

close all;

plot(ty(:,1),t,ty(:,2),'k:' linewidth’,2);

xlabel('time(s));ylabel('yd,y');

legend('Ideal position signal','Position tracking');s

通过本实例的仿真可见，采用S函数，很容易地表示复杂的被控对象及控制算法，特别适合于复杂控制系统的仿真。