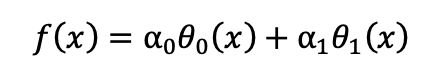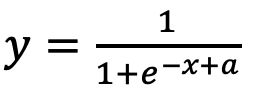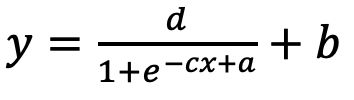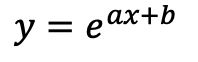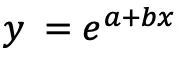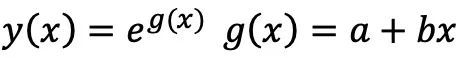如何优雅的拟合非线性曲线

这次真的和阿猪老师学到了，深度学习降维打击数据拟合竟然是这么的高效！

---

某天下班，小洛在微信上忽然呼叫我：

我一看好家伙，这不是手到擒来？这也太简单了，直接开整：

一、curve_fit函数拟合

众所周知，scipy就可以进行曲线拟合，直接开整：

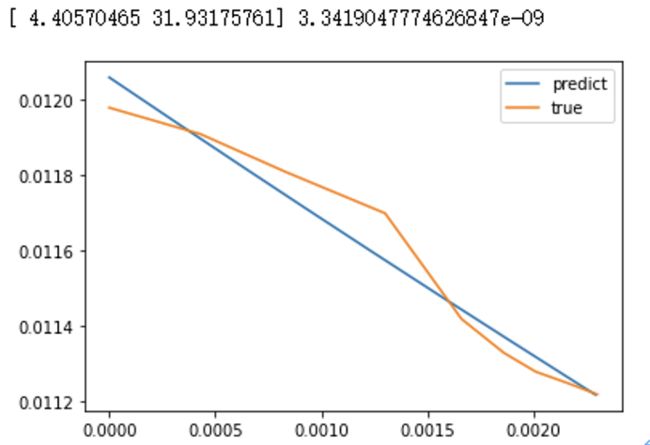
输出效果：

某位同学一头雾水：我要的是非线性的函数，为啥出来的是一条直线？还相差这么远？

二、这个表达式是合理的吗？

优化的第一步：可以看到函数内的-b*(x-a) 首先就可以被简化成bx+a，来把参数合并掉(冷知识，在这里其实无所谓参数的正负号，优化方法会自动去进行拟合的)

输出：

这一个简单的改动，直接让mse从8e-8下降到3e-9,约20倍。

问：为什么拟合的曲线还是一条直线，不是小洛同学想要的那条曲线？

答：因为curve_fit函数使用最小二乘法对函数进行拟合，适用的范围仅为使用线性参数组合的非线性函数，例如：

其中的a0、a1即为可以拟合的参数，θ0(x)则是非线性的某些函数，而小洛给出的sigmoid的函数形式并不是这样，因此用curve_fit拟合出来的效果并不让人满意。

高中生涯渐渐远去，相信同学们的数学知识忘得也差不多了，在这里简单地提一下函数拟合中需要注意的问题：

1、函数的零点、缩放参数

例如sigmoid的原始形式为：

在x=0的时候y取得0.5. 如果想要在x轴上做左右平移，就需要把x替换成x+a的形式，成为：

而在y轴上做上下平移，同样地要在y替换成y+b的形式；还有横向、纵向的拉伸，也对应了x需要替换成c*x, y需要替换成d*y 。因为期待被拟合的参数自行决定正负，所以放分子和分母都没关系；经过项式调整，我们形成了最终表达式，对于原先sigmoid函数而言，这个格式可以支持平移和缩放的形式：

我们把原先公式改写为上面的公式套进去，再用curve_fit优化输出：

可以看到mse进一步下降到2e-9，也终于有了一点点的曲线样子，然鹅还有很大提升空间。

2、函数的定义域

如果所选用的函数对定义域有要求，比如选用典型的对数函数log(x) ，y=log(ax+b)的时候。要复习一下数学知识，知道对数函数的定义域（也就是此处ax+b的范围），要求是大于0的，但是我们给出的这个形式并不能保证ax+b一定大于0，就会超出计算范围，各大计算库此时会返回nan，此时可以在ax+b外面加一个绝对值。

3、函数的值域

小洛要拟合的sigmoid除了非线性的特点，还要注意一个问题：它的值域，也就是y能够抵达的范围。这里如果我们确定定义域的范围是固定的范围内还好，就可以把最终拟合的值域全部算出来。原始sigmoid的值域是0~1范围内，因此就算给y加上了缩放，最终也只能到达0~c的范围内

在寻常的非线性函数的拟合里，如果需要继续使用curve_fit，就需要将其转化为线性的形式，例如指数函数：

它的拟合可以取对数，让其对lny~x的关系进行拟合：

看来，curve_fit函数并不能用来很好的拟合sigmoid函数，即使表达式已经已经优化到最终格式，拟合出的却还是只有微微的曲线，并不是sigmoid曲线的样子。要强行用curve_fit的话只能做更复杂的变换去依靠中间表达式去间接拟合。

（那么，能不能再给力一点，这个好复杂啊不懂.jpg）

三、非线性函数拟合的通用解决法

当然对于很多同学们来说，会发现继续用curve_fit函数，把非线性函数转化为若干参数与函数的乘法逻辑过于复杂，超出了自己的数学能力，那能不能有一个更通用、简单的方式去解决呢？

当然有！

作为一名工作在人工智障领域的算法工程师，现在的名词“深度学习”正是为了解决超级复杂的非线性问题而产生的，深度学习的模型正是非线性的典型代表。这个非线性已经叠加到了人类无法用手动去对公式进行优化的复杂度。

非线性导致深度学习在处理深层次的信息上，性能非常优异，在图像识别、图文理解这些领域，都得到了超越人类的特性；我们现在看到的各种商品、图文、短视频，最终也是靠深度学习，计算出这些单品的向量，再和我们自身的兴趣向量做运算，影响了搜索、推荐时的排序。

（深度学习.blingbling.jpg）

小洛这次仅仅只要拟合这个sigmoid非线性函数，但如果下次是其他曲线的函数的话，就又要经过其他的手工的表达式变化与复杂的构造，这样不行！

在这里，我们可以使用深度学习里的优化原理，找到一个针对非线性模型拟合的通用解决方法，这里使用torch进行优化。

首先我们对函数进行少量的改动，其中包含了我们前面说的平移、缩放的内容，因此带来了4个参数：

所有深度学习优化的原理都是一样，其中核心规则很简单：

1、对计算进行求(偏)导

例如y=a+bx 我们要知道每个参数对于最终输入的y产生了多大的作用，就是求参数a对于y的偏导（理解为此处的a的变化，会带来多大的y的变化）

2.使用链式法则进行导数的传递

例如复合函数：

是复合函数：

的传递，链式法则告诉我们，这样的复合函数求导遵循规则：

参数a对于y的导数，等于复合函数g对y的导数乘以 a对函数g的导数；以此类推，嵌套的复合函数就这样依次传递下来即可；

3.知道真值和预测值的差异

（小洛此处定义为mse），我们平常意义上也即定义为损失。可以由此计算各个参数的导数，那么参数们沿着最小化损失的方向迈进，就可以让损失降低。这在深度学习里通过优化器的方式来进行。

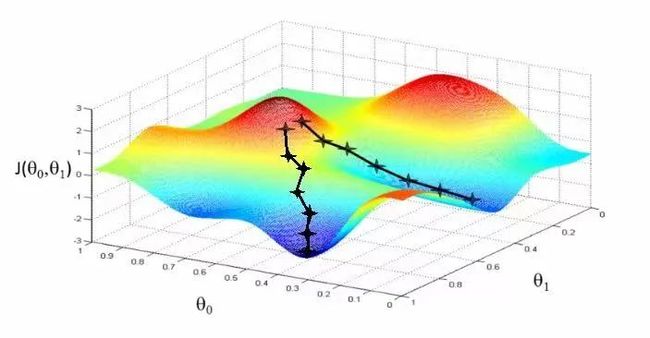
这几个规则组合到一起，也就是传说中的SGD梯度下降法：

当然实际的算法中使用的是改进的一个优化器Adam，我们加一点点细节，写出如下代码（其中用来优化函数参数的代码甚至也就10行）：

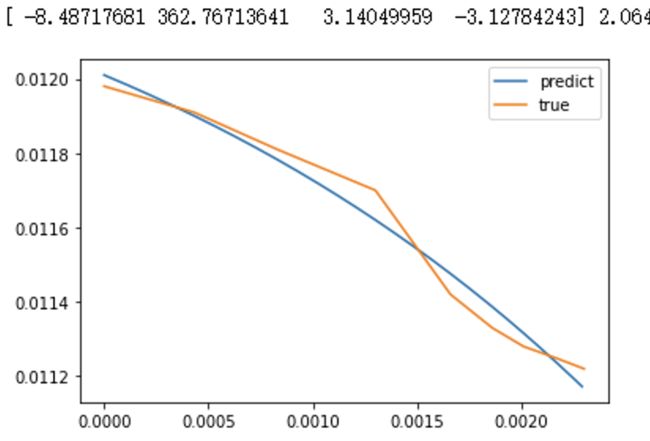
输出效果非常美好，完美回答了小洛的问题：

四、为什么效果还差一点？

虽然目前已经完美的回答了小洛的sigmoid拟合问题。但实际使用上，可能大家还是会遇到一些不完美的情况。一种情况是前置没有设计好需要拟合的函数，导致函数的作用域和定义域出现问题，与实际的数据不匹配；另一种则是代码中涉及的超参了；

这里有几个比较魔法的数字，我们来讲一下这些魔法的原理：

1、为什么有个bigger参数

因为x和y的范围都很小，尤其是y，在0.01范围内，这个范围假如一个函数的预测始终输出0.012，最后的mse一平方，会直接落到1e-7范围以内，这个数字太小了，以至于低于了许多计算中eps的范畴（一个例子是为了避免除以0，除法会成为1/(x+eps)），这会导致函数难以进行有效的优化。

2、Learning rate为什么是0.002

这个叫做学习率的参数，在实际的应用场景中也需要在一定的范围内进行调整。前面我们说到，这个是优化器根据参数的梯度，往前前进的步长，因此这个步长跟实际的非线性函数的特点相关；举个例子：我们知道x^2函数的导数是x，所以在x=2处导数是2，步长决定了我要往最小化损失的地方迈多远，比如此时如果学习率是2，下一次我会迈往x=2-2*2=-2 的位置，这样就很难迈向函数的最小值部分了。

3、StepLR起到一个什么作用？为什么是0.8

一般来说，优化到了后面，需要一个更保守的步长，这个可以通过观察loss的下降情况来进行调整。

比如小洛遇到的另一个案例问题：（和上面的案例不同，这次是要拟合log函数曲线）

她这个拟合出来的曲线就不是很棒棒。这个一来可以对上面的超参学习率进行调整。二来还可以调整下公式，看看是不是在函数本身之外，再加个线性的部分比如y=log(ax+b)+cx+d之类的。

聪明的小洛已经很快地学会了，同学们也都可以一起用起来这个可以适用于任意数据函数拟合的万能方法啦！

End