Lecture 1_Extra Classification Probabilistic Generative Model

Lecture 1_Extra Classification: Probabilistic Generative Model

Classification: Probabilistic Generative Model

分类的概念

分类要找一个 $function$ 函数，输入对象 $x$ 特征， 输出是该对象属于 $n$ 个类别中是属于哪一个。

• 例子1：信用评分【二分类问题】
  • 输入：收入，储蓄，行业，年龄，金融史…
  • 输出：是否拒绝拒绝贷款
• 例子2：医疗诊断【多分类问题】
  • 输入：当前症状，年龄，性别，医疗史…
  • 输出：患了哪种疾病
• 例子3：手写文字辨识【多分类问题】
  • 输入：手写的文字
  • 输出：约9353个汉字中输入哪一个

• 例子4：人脸识别【多分类问题】
  • 输入：不同人脸的图片
  • 输出：人名

Pokemon 属性预测

需要找到一个函数 $function$ 能够预测出 Pokemon 的属性（电、水、草，等等）

首先需要量化 Pokemon：

• Total：整体强度；
• HP：生命值；
• Attack：攻击力；
• Defense：防御力；
• SP Atk：特殊攻击力；
• SP Def：特殊防御力；
• Speed：速度；

所以，一只 Pokemon 能够用上述 $7$ 个属性来度量，用这 $7$ 个数值组成的向量来表示一只 Pokemon。

为什么需要预测 Pokemon 的属性呢？—— 不同属性的 Pokemon 间存在克制关系（）：

如何做分类

训练数据

Classification as Regression?

假设还不了解怎么做，但之前已经学过了 $regression$。就把分类当作回归硬解。
举一个二分类的例子，假设输入神奇宝贝的特征 $x$，判断属于类别 $1$ 或者类别 $2$，把这个当作回归问题。

• 类别 $1$：相当于target是 $1$。
• 类别 $2$：相当于target是 $-1$。

然后训练模型：因为是个数值，如果数值比较接近 $1$，就当作类别 $1$，如果数值接近 $-1$，就当做类别 $2$。这样做遇到什么问题？

这样用回归的方式硬训练可能会得到右图中紫色的这条。直观上就是将绿色的线偏移一点到紫色的时候，就能让右下角的那部分的值不是那么大了。但实际是绿色的才是比较好的，用回归硬训练并不会得到好结果。此时可以得出用回归的方式定义，对于分类问题来说是不适用的。

还有另外一个问题：比如多分类。类别 $1$ 当作target1，类别 $2$ 当作target2，类别 $3$ 当作target3…如果这样做的话，就会认为类别 $2$ 和类别 $3$ 是比较接近的，认为它们是有某种关系的；认为类别 $1$ 和类别 $2$ 也是有某种关系的，比较接近的。但是实际上这种关系不存在，它们之间并不存在某种特殊的关系。这样是没有办法得到好的结果。

理想模型

• 先看二分类，将 $function$ 中内嵌一个函数 $g(x)$，如果大于 $0$，就认为是类别 $1$，否则认为是类别 $2$；
• 损失函数的定义就是，如果选中某个 $funcitonf(x)$，在训练集上预测错误的次数。当然希望错误次数越小越好。但是这样的损失函数没办法解，这种 Loss 的定义没办法微分；
• 是有解决方法的，比如 Perceptron 和 SVM。本节先考虑一种概率模型。

一些简单的概率

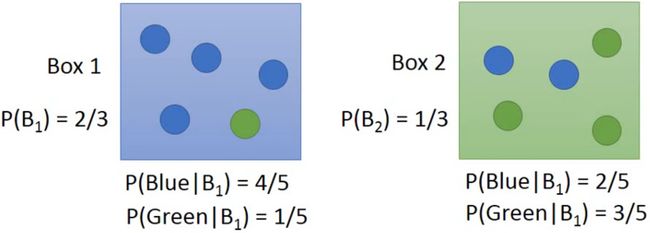
说明：假设两个盒子，各装了 $5$ 个球，还得知随机抽一个球，抽到盒子 $1$ 的球的概率是 $2/3$，抽到盒子 $2$ 的球的概率是$1/3$。从盒子中蓝色球和绿色球的分配可以得到：

• 在盒子 $1$ 中随机抽一个球，是蓝色的概率为 $4/5$，绿的的概率为 $1/5$；
• 在盒子 $2$ 中随机抽一个球，是蓝色的概率为 $2/5$，绿的的概率为 $3/5$。

现在求随机从两个盒子中抽一个球，抽到的是盒子 $1$ 中蓝色球的概率是多少？
$$\begin{array}{rl}P(B_1|Blue)& =\frac{P(Blue|B_1)P(B_1)}{P(Blue|B_1)P(B_1)+P(Blue|B_2)P(B_2)}\\ & =\frac{\frac{4}{5}\ast \frac{2}{3}}{\frac{4}{5}\ast \frac{2}{3}+\frac{2}{5}\ast \frac{1}{3}}\\ & =\frac{4}{5}\end{array}$$

概率与分类的关系

那么，两个盒子中抽一个球，抽到的是盒子 $1$ 中蓝色球的概率是多少？相当于从两个类别 $class$ 中抽一个 $x$，抽到的是类别 $1$ 中 $x$ 的概率是多少？可以转化成，随机给出一个 $x$，那么它属于哪一个类别（属于概率相对比较大的类别）？

同理知道红色方框的值，就可以计算出给一个 $x$，它是属于哪个类型的。$P(C_1|x)$ 和 $P(C_2|x)$，哪个类别的概率大就属于哪个类别。接下来就需要从训练集中估测红色方框中的值。这一套想法叫做生成模型（Generative Model）。因为有了这个模型，就可以生成一个 $x$，可以计算某个 $x$ 出现的概率，知道了$x$ 的分布，就可以自己产生 $x$ 。

先验概率（Prior）

先考虑简单的二分类，水属性或者一般属性，通过训练集的数据可以计算出 $P(C_1)$ 和 $P(C_2)$，如图所示：

• 水属性占比：$P(C_1)=0.56$
• 普通属性占比：$P(C_2)=0.44$

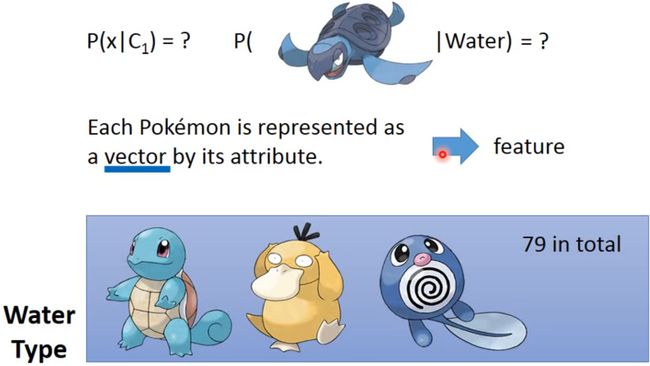
下面想计算 Pokemon 原盖海龟是水属性的概率，即 $P(x|C_1)$。虽然知道这是一只原盖海龟，一看就是水属性的，但是在模型中，我们输入的是一个特征向量（vector）。

也就是在水系的神奇宝贝中随机选一只，是原盖海龟的概率。下面将训练集中 $79$ 个水系的神奇宝贝，属性Defense和SP Defense进行可视化:

这里假设这 $79$ 点是从高斯分布（Gaussian distribution）中采样的，现在需要从这 $79$ 个点找出符合的那个高斯分布。

高斯分布（Gaussian distribution）

简单点可以把高斯分布当作一个 $function$，输入就是一个向量 $x$ ，输出就是选中 $x$ 的概率（实际上高斯分布不等于概率，只是和概率成正比，这里简单说成概率）。$function$由期望 $\mu$ 和协方差矩阵 $\Sigma$ 决定。

上图的例子是说同样的 $\Sigma$，不同的 $\mu$，概率分布的最高点的位置是不同的。下图的例子是同样的 $\mu$，不同的 $\Sigma$，概率分布的最高点是一样的，但是离散度是不一样的。

假设通过 $79$ 个点估测出了期望 $\mu$ 和协方差矩阵 $\Sigma$。期望是上图中的黄色点，协方差矩阵是红色的范围。现在给一个不在 $79$ 个点之内的新点，用刚才估测出的期望和协方差矩阵写出高斯分布的 $function{f}_{\mu ,\Sigma }(x)$，然后把 $x$ 带进去，计算出被挑选出来的概率。

极大似然估计（Maximum Likelihood）

首先对于这 $79$ 个点，任意期望和协方差矩阵构成的高斯分布，都可以生成这些点。当然，像上图中左边的高斯分布生成这些点，比右边高斯分布生成这些点的几率要大。那给一个 $\mu$ 和 $\Sigma$，它生成这 $79$ 个点的概率为图中的 $L(\mu ,\Sigma )$，$L(\mu ,\Sigma )$ 也称为样本的似然函数。

使得 $L(\mu ,\Sigma )$ 最大的 $(\mu ,\Sigma )$ 记做 $({\mu }^{\ast },{\Sigma }^{\ast })$ 。

算出之前水属性和一般属性 Pokemon 高斯分布的期望和协方差矩阵的最大似然估计值 ${\mu }^{\ast },{\Sigma }^{\ast }$：

分类模型

接下来，进行分类，分类结果如下：

结果不是很理想。

模型优化

通常来说，不会给每个高斯分布都计算出一套不同的最大似然估计，协方差矩阵是和输入 feature 大小的平方成正比，所以当 feature 很大的时候，协方差矩阵是可以增长很快的。此时考虑到 model 参数过多，容易Overfitting，为了有效减少参数，给描述这两个类别的高斯分布相同的协方差矩阵。

此时修改似然函数为 $L({\mu }_1,{\mu }_2,\Sigma )$。${\mu }_1,{\mu }_2$ 计算方法和上面相同，分别加起来平均即可；而 $\Sigma$ 的计算有所不同。

这里详细的理论支持可以查看《Pattern Recognition and Machine Learning》Christopher M. Bishop 著，chapter4.2.2

右图新的结果，分类的 boundary 是线性的，所以也将这种分类叫做 linear model。如果考虑所有的属性，发现正确率提高到了 $73\%$。

概率生成模型建模步骤

将上述问题简化为前几个系列说过的三大步：

为什么选择高斯分布？

• 假设每一个维度用概率分布模型产生出来的几率是相互独立的，所以可以将 $P(x|C_1)$ 拆解。可以认为每个 $P(x_k|C_1)$ 产生的概率都符合一维的高斯分布，也就是此时 $P(x|C_1)$ 的高斯分布的协方差是对角型的（不是对角线的地方值都是0），这样就可以减少参数的量。但是试一下这种做法会坏掉。
• 对于二元分类来说，此时用通常不会用高斯分布，可以假设是符合 Bernoulli distribution（伯努利分布）；
• 假设所有的 feature 都是相互独立产生的，这种分类叫做 Naive Bayes Classifier（朴素贝叶斯分类器）。

后验概率 Posterior Probability

如上图所示，将 $P(C_1|x)$ 整理，得到一个 $\sigma (z)$，这叫做 Sigmoid function。

接下来，求解 $z$

如上图所示，已经求得了 $z$。在实际应用中协方差矩阵是同一个矩阵，因此：

$P(C_1|x)=\sigma (w\cdot x+b)$，从这个式子也可以看出上述当共用协方差矩阵的时候，为什么分界线是线性的。

中协方差矩阵是同一个矩阵，因此：

$P(C_1|x)=\sigma (w\cdot x+b)$，从这个式子也可以看出上述当共用协方差矩阵的时候，为什么分界线是线性的。

既然这里已经化简为上述的式子，直观感受就是可以直接估测 $w,b$ 就可以直接得到结果了。