一起读论文 | Complex-order: 一种新的位置编码方式

导读：今天分享一篇华人学者发表在顶会ICLR 2020上的论文《Encoding Word Order in Complex Embeddings》，主要对序列建模的位置信息编码方法进行研究。可以阅读先前的文章《一文读懂Transformer模型中的位置编码》对其中的一种位置信息编码方式的深入分析。本文认为先前的方法需要独立训练每个位置向量，而且也不能建模序列的邻接或者优先关系。本文把这种问题称之为position independence problem。为此，本文提出了一种新颖的方法Complex-order来解决这样的问题。

点评：本文的idea非常简单清晰，带来的效果提升也非常明显，文中的证明推导也非常棒，研究工作非常具有创新性，值得一读。作者开源了实现代码，有兴趣的朋友可以跑一边实验。

研究背景及动机

语言是有顺序的。神经网络在建模这种顺序结构时，因为难以并行化处理，使得计算代价变得非常地高。通过在特征级别上添加position embeddings而不是在神经网络架构上对词的顺序进行建模已经可以减轻这样的问题（参考对位置编码的详细解读），比如Gehring等人的ConvSeq与Vaswani等人著名的Transformer模型。先前的研究工作通过引入额外的位置编码，在Embedding层将词向量与位置向量相加进行融合：

$$f(j,pos)=f_{we}(j)+f_{pe}(pos)$$

但是，这种方法只接受整型数值作为词索引或位置索引，每个词或位置都只能通过独立训练得到。这对每个词向量是合理的，因为词的索引是建立在给定的词典的顺序之上的。但这种方法不能捕捉 ordered relationship（邻接或优先关系），会导致每个位置上的位置向量是彼此独立的，作者称之为position independence problem。这种问题对于位置不敏感的神经网络（如FastText，ConvSeq及Transformer）来说变得尤为重要。

研究内容及方法

本文主要对序列建模的位置信息编码进行研究，针对先前的研究方法可能导致的position independence problem，本文提出了一种非常新颖的改进方法——Complex order——对词的这种全局绝对位置及它们的内在顺序及邻接关系进行建模。这样的话，Gehring等人提出的_position-independent_的位置向量可以被认为是该方法在独立变量上的特例。

作者将每个词嵌入扩展为一个自变量为位置 $pos$ 的一个连续函数，好处在于词表示可以随着位置的变化而平滑地移动，不同位置上的词表示就可以互相关联起来。函数定义如下：

$$f(j,pos)={\text{g}}_j(pos)\in {\mathbb{R}}^D$$

其中，$f(j,pos)$ 表示此表中序号为 $j$ 的单词在位置 $pos$ 上的单词向量，${\mathbf{g}}_j$ 是 ${\mathbf{g}}_{we}(j)\in (\mathcal{F}{)}^D$ 的缩写，$D$ 表示函数集合，$g_{we}(\cdot )$：$\mathbb{N}\to (F{)}^D$表示单词索引到函数的映射。展开为：

$$[g_{j,1}(pos),g_{j,2}(pos),\cdots ,g_{j,D}(pos)]\in {\mathbb{R}}^D$$

对于任意的 $g_{j,d}(\cdot )\in \mathcal{F}$ : $\mathbb{N}\to \mathbb{R}$，$d\in \{1,2,\cdots ,D\}$，都是关于位置索引$pos$的一个函数。在无需改变函数 ${\mathbf{g}}_j$ 的情况下，只需要替换一下变量 $pos$ 就可以实现把词 $w_j$ 从当前位置 $pos$ 移动到另一个位置 $po{s}^{\prime }$。

为了达到上述要求，函数需要满足以下两条性质：

Property 1. Position-free offset transformation:

存在变换函数Transform : $\mathbb{N}\times \mathbb{C}\to \mathbb{C}$，使得对于任意位置 $pos\in \mathbb{N}$ 和 $n>1$，Transform${}_n(\cdot )$=Transform$(n,\cdot )$满足：

$$g(pos+n)={\text{Transform}}_n(g(pos))$$

作者把这样的函数Transform称之为witness。论文只考虑线性变换，即每个Transform${}_n$是一个线性函数。

Property 2. Boundedness:

关于位置变量的函数应该是有界的，也就是：

$$\exists \delta \in {\mathbb{R}}^{+},\forall \text{pos}\in \mathbb{N},|g(\text{pos})|\le \delta$$

作者给出了满足上述两条性质的解函数的形式：

$$g(pos)=z_2{z}_1^{pos}for{z}_1,z_2\in \mathbb{C}with|z_1|\le 1$$

证明如下:

对于任意位置 $n_1，n_2\in \mathbb{N}$，有

$$\begin{array}{lcc}w(n_1)w(n_2)g(pos)& =& w(n_2)g(pos+n_1)\\ & =& g(pos+n_1+n_2)\\ & =& {\text{Transform}}_{n_1+n_2}(g(pos))\\ & =& w(n_1+n_2)g(pos)\end{array}$$

因此有 $w(n_1+n_2)=w(n_1)w(n_2)$。令 $w(1)=z_1$，$g(0)=z_2$，因为 $n_1$，$n_2$ 是任意的，因此对于所有的 $n\in \mathbb{N}$，都有

$$w(n)=(w(1){)}^n=z_1^n$$

$$g(pos+n)=w(n)g(pos)=z_1^{n}g(pos)$$

而且，当 $pos\ge 1$，我们有 $g(pos)=g(1+pos-1)=w(pos)g(0)=z_1^{pos}{z}_2=z_2{z}_1^{pos}$。对于 $pos=0$，$g(0)=z_2=z_{2}z{1}^0$，因此有 $g(pos)=z_2{z}_1^{pos}$。

当 $|z_1|>1$，$g(pos)$ 就不是有界函数，因此限制 $|z_1|\le 1$，此时，$|g(pos)|\le |z_2{z}_1^{pos}|\le |z_2||z_1^{pos}|\le |z_2|$，函数 $g$ 就是有界的。

又由 $w(n)=z_1^n$ 和 Transform${}_n(pos)=w(n)pos$，对所有的位置 $pos$，得

$$g(pos+n)=z_2{z}_1^{pos+n}=z_2{z}_1^{pos}{z}_1^n=g(pos)z_1^n={\text{Transform}}_n(g(pos))$$

得证。

对于任意的 $z\in \mathbb{C}$，我们可以写成 $z=r{e}^{i\theta }=r(\cos \theta +i\sin \theta )$。因此，可以简化为

$$g(pos)=z_2{z}_1^{pos}=r_2{e}^{i{\theta }_2}(r_1{e}^{i{\theta }_1}{)}^{pos}=r_2{r}_1^{pos}{e}^{i({\theta }_2+{\theta }_{1}pos)}subjectto|r_1|\le 1$$

在实现过程中，由于上述 $|r_1|\le 1$的限制，函数$g$的上述定义会导致优化问题，因此一种自然而简单的避免这个问题的方法就是固定 $r_1=1$，那么 $|e^{ix}|\equiv 1$，上式就可以简化为：

$$g(pos)=r{e}^{i(w\text{pos}+\theta )}$$

最终的embedding表示为：

$$\begin{array}{ccc}f(j,pos)& =& {\mathbf{g}}_j(pos)={\mathbf{r}}_j{e}^{i(w_{j}pos+{\theta }_j)}\\ & =& [r_{j,1}{e}^{i(w_{j,1}pos+{\theta }_{j,1})},\cdots ,r_{j,2}{e}^{i(w_{j,2}pos+{\theta }_{j,2})},\cdots ,r_{j,D}{e}^{i(w_{j,D}pos+{\theta }_{j,D})}]\end{array}$$

其中，每个坐标点 $d(1\le d\le D)$都有各自的参数：振幅 $r_{j,d}$ 、周期 $p_{j,d}$ 、初相 ${\theta }_{j,d}$ ，这三个参数都是需要学习的参数。表示作者将这种新的编码方式称为 general complex-valued embedding (通用复数值嵌入)。

实验及结果

作者主要在文本分类、机器翻译及语言建模三个任务上对这种新的位置编码进行了评估。

1. 文本分类

实验设置

数据集：采用CR、MPQA、SUBJ、MR、SST、TREC等五个常用数据集，数据集统计如下：

基准方法：选择Fasttext、CNN、LSTM、Transformer等四种神经网络模型，为每个模型分别进行以下四种配置：（1）不使用位置编码；（2）Gehring等人的Vanilla Position Embeddings (PE)；（3）Vaswani等人的Trigonometric Position Embeddings (TPE)；（4）Wang等人的Complex-vanilla word embeddings；（5）本文提出的位置感应的复数值词嵌入Complex-order。

实验结果如下：

时间消耗对比结果如下：

作者还在Transformer模型上进行了消融性测试，结果如下表所示：

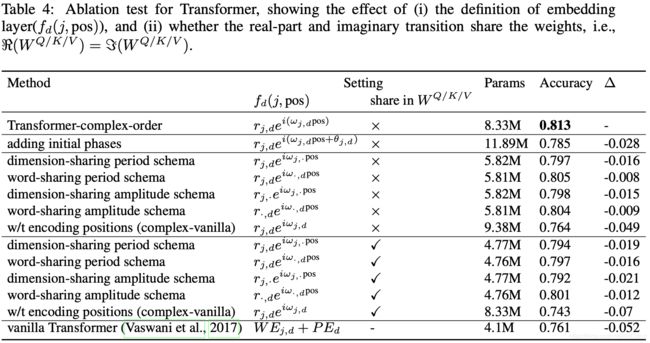
2. 机器翻译

数据集：WMT 2016 English-German数据集

基准方法：（1）basic Attentional encoder-decoder (AED)；（2）AED with Byte-pair encoding (BPE) subword segmentation for open-vocabulary translation；（3）AED with extra linguistic features；（4）本文的Transformer Complex-order

3. 语言建模

数据集：text8（English Wikipedia articles）

基准方法：BN-LSTM，LN HM-LSTM RHN，Large mLSTM

实验结果如下：

---

想要了解更多的自然语言处理最新进展、技术干货及学习教程，欢迎关注微信公众号“语言智能技术笔记簿”或扫描二维码添加关注。