计算机视觉面试(四)
计算机视觉面试(四)
1.手撕NMS
在现有的基于anchor的目标检测算法中,都会产生数量巨大的候选矩形框,这些矩形框有很多是指向同一目标,因此就存在大量冗余的候选矩形框。非极大值抑制算法的目的正在于此,它可以消除多余的框,找到最佳的物体检测位置。
实现步骤如下:
1.设定目标框的置信度阈值,常用的阈值是0.5左右
2.根据置信度降序排列候选框列表
3.选取置信度最高的框A添加到输出列表,并将其从候选框列表中删除
4.计算A与候选框列表中的所有框的IoU值,删除大于阈值的候选框
5.重复上述过程,直到候选框列表为空,返回输出列表
代码:
def nms(bounding_boxes, Nt):
if len(bounding_boxes) == 0:
return [], []
bboxes = np.array(bounding_boxes)
# 计算 n 个候选框的面积大小
x1 = bboxes[:, 0]
y1 = bboxes[:, 1]
x2 = bboxes[:, 2]
y2 = bboxes[:, 3]
scores = bboxes[:, 4]
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
# 对置信度进行排序, 获取排序后的下标序号, argsort 默认从小到大排序
order = np.argsort(scores)
picked_boxes = [] # 返回值
while order.size > 0:
# 将当前置信度最大的框加入返回值列表中
index = order[-1]
picked_boxes.append(bounding_boxes[index])
# 获取当前置信度最大的候选框与其他任意候选框的相交面积
x11 = np.maximum(x1[index], x1[order[:-1]])
y11 = np.maximum(y1[index], y1[order[:-1]])
x22 = np.minimum(x2[index], x2[order[:-1]])
y22 = np.minimum(y2[index], y2[order[:-1]])
w = np.maximum(0.0, x22 - x11 + 1)
h = np.maximum(0.0, y22 - y11 + 1)
intersection = w * h
# 利用相交的面积和两个框自身的面积计算框的交并比, 将交并比大于阈值的框删除
ious = intersection / (areas[index] + areas[order[:-1]] - intersection)
left = np.where(ious < Nt)
order = order[left]
return picked_boxes
更多nms可以阅读参考文章:https://blog.csdn.net/lz867422770/article/details/100019587
2.手撕ResNet残差块
首先Resnet 结构图如下图所示:
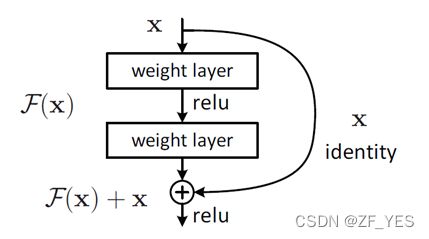
F ( x l , w f ) = x l + H ( x l , w L ) F(x_l,w_f)=x_l+H(x_l,wL) F(xl,wf)=xl+H(xl,wL)
x l x_l xl是第 l l l曾的输入, w l = { w l , k ∣ 1 < = k < = K } w_l=\{w_{l,k}|1<=k<=K\} wl={wl,k∣1<=k<=K}是第 l l l层的参数, K K K是残差单元层数
那么第 l + 1 l+1 l+1层的输入,
x l + 1 = F ( x l , w f ) x_{l+1}=F(x_l,w_f) xl+1=F(xl,wf)
因此得到
x l + 1 = x l + H ( x l , w l ) x_{l+1}=x_l+H(x_l,w_l) xl+1=xl+H(xl,wl)
循环带入到这个式子
x l + 2 = x l + 1 + H ( x l + 1 , w l + 1 ) = x l + H ( x l , w l ) + H ( x l + 1 , w l + 1 ) x_{l+2}=x_{l+1}+H(x_{l+1},w_{l+1})=x_l+H(x_l,w_l)+H(x_{l+1},w_{l+1}) xl+2=xl+1+H(xl+1,wl+1)=xl+H(xl,wl)+H(xl+1,wl+1)
我们可以得到 x l = x l + ∑ i = l L − 1 F ( x i , w i ) x_l=x_l+\sum_{i=l} ^{L-1}F(x_i,w_i) xl=xl+∑i=lL−1F(xi,wi) (1)
对于任何深度的L来讲,上述式子(1)显示了一些良好的特性。
(1)第 L L L层的特征 x L x_L xL可以分为两个部分,第一部分是浅层的网络表示 x l x_l xl加上一个残差函数映射 ∑ i = l L − 1 F ( x i , w i ) \sum_{i=l} ^{L-1}F(x_i,w_i) ∑i=lL−1F(xi,wi),表明模型在任意单元内都是一个残差的形式。
(2)对于任意深度 L L L的特征 x L x_L xL 来讲,它是前面所有残差模块的和,这与简单的不加短连接的网络完全相反。原因是,不加短连接的网络在第 L L L层的特征 x L x_L xL是一系列的向量乘的结果,即 ∏ i = 1 L − 1 W i x 0 \prod_{i=1}^{L-1} W_{i}x_0 ∏i=1L−1Wix0(在忽略batch normalization和激活函数的情况下)。
同样,上述式子显示有非常好的反向传播特性,假设损失为 e e e ,根据链式求导法则,我们可以得到:
∂ e ∂ x l = ∂ e ∂ x L ∂ x L ∂ x l = ∂ e ∂ x L ( 1 + ∂ ∂ x l ∑ i = 1 L − 1 F ( x i , w i ) ) \frac{\partial e}{\partial x_l}=\frac{\partial e}{\partial x_L} \frac{\partial x_L}{\partial x_l}=\frac{\partial e}{\partial x_L}(1+\frac{\partial }{\partial x_l}\sum_{i=1}^{L-1}F(x_i,w_i)) ∂xl∂e=∂xL∂e∂xl∂xL=∂xL∂e(1+∂xl∂∑i=1L−1F(xi,wi))
显示梯度 ∂ e ∂ x L \frac{\partial e}{\partial x_L} ∂xL∂e由两个部分组成,一部分 ∂ x L ∂ x l \frac{\partial x_L}{\partial x_l} ∂xl∂xL 是不用经过任何权重加权的信息流,另一部分是通过加权层的 ∂ e ∂ x L ( ∂ ∂ x l ∑ i = 1 L − 1 F ( x i , w i ) ) \frac{\partial e}{\partial x_L}(\frac{\partial }{\partial x_l}\sum_{i=1}^{L-1}F(x_i,w_i)) ∂xL∂e(∂xl∂∑i=1L−1F(xi,wi)) ,两部分连接的线形特性保证了信息可以直接反向传播到浅层。同时式子还说明对于小的batch而言,梯度 ∂ e ∂ x l \frac{\partial e}{\partial x_l} ∂xl∂e不太可能会消失,因为通常 对于小的batch来讲不会总是为1,那么这表示即使权重非常小,梯度也不会为0,不存在梯度消失的问题。
class BasicBlock(nn.Module):
expansion = 1
def __init__(self, inplanes, planes, stride=1, downsample=None): # inplanes代表输入通道数,planes代表输出通道数。
super(BasicBlock, self).__init__()
self.conv1 = conv3x3(inplanes, planes, stride)
self.bn1 = nn.BatchNorm2d(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.bn2 = nn.BatchNorm2d(planes)
self.downsample = downsample
self.stride = stride
def forward(self, x):
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
if self.downsample is not None:
residual = self.downsample(x)
out += residual
out = self.relu(out)
return out
3.常用的边缘提取算子
滤波的目的主要两个:
1.通过滤波来提取图像特征,简化图像所带的信息作为后续其它的图像处理
2.为适应图像处理的需求,通过滤波消除图像数字化时所混入的噪声
其中第一点就是边缘检测中所使用的基本思想,即简化图像信息,使用边缘线代表图像所携带信息
滤波可理解为滤波器(通常为33、55矩阵)在图像上进行从上到下,从左到右的遍历,计算滤波器与对应像素的值并根据滤波目的进行数值计算返回值到当前像素点,听起来是不是很像卷积运算。
在介绍完滤波的知识后,学习基本边缘检测算法是一件很轻松的事情,因为边缘检测本质上就是一种滤波算法,区别在于滤波器的选择,滤波的规则是完全一致的
常用的边缘算子:Sobel、Roberts、canny算子
sobel算子
#include
using namespace cv;
int main()
{
Mat dstIamge, grad_x, grad_y, abs_grad_x, abs_grad_y;
Mat srcIamge = imread("D:\\image.png");//绝对路径(完整路径)
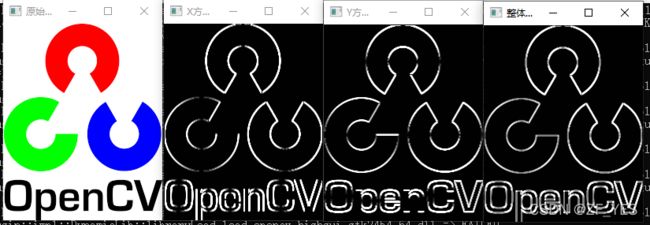
imshow("原始图", srcIamge);
cvtColor(srcIamge, srcIamge, COLOR_RGB2GRAY);
//求 X方向梯度
Sobel(srcIamge, grad_x, CV_16S, 1, 0, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_x, abs_grad_x);//使用线性变换转换输入数组元素成8位无符号整型
imshow("X方向Sobel", abs_grad_x);
//求Y方向梯度
Sobel(srcIamge, grad_y, CV_16S, 0, 1, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_y, abs_grad_y);
imshow("Y方向Sobel", abs_grad_y);
//合并梯度(近似)
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0,dstIamge);
imshow("整体方向Sobel", dstIamge);
waitKey(0);
return 0;
}
Robert算子是图像边缘查找的最简单应用,该算子要是水平和垂直方向的2*2矩阵。

Roberts算子是一种斜向偏差分的梯度计算方法,梯度的大小代表边缘的强度,梯度的方向与边缘的走向垂直(正交)。
优缺点
从图像处理的实际效果来看,计算简单,边缘定位较准,但对噪声极敏感。适用于边缘明显且噪声较少的图像分割。
#include
#include // 核心组件
#include // GUI
#include // 图像处理
using namespace cv;
using namespace std;
void show_image(Mat image)
{
imshow("test", image);
waitKey(0);
}
void main()
{
Mat image;
image = imread("C:/Users/Dell/Desktop/images.png", 0);
show_image(image);
int height = image.rows;
int width = image.cols;
int step = image.step;
for (int i = 1; i < height - 1; i++)
{
uchar* updata = image.ptr(i);
uchar* updata1 = image.ptr(i + 1);
for (int j = 1; j < width - 1; j++)
{
updata[j] = updata[j] - updata1[j + 1];
updata[j] = -updata[j + 1] + updata1[j];
if (updata[j] < 0)
{
updata[j] = 0;
}
if (updata[j] > 255)
{
updata[j = 255];
}
}
}
show_image(image);
}
Canny算子
Canny算子是澳洲计算机科学家约翰·坎尼(John F. Canny)于1986年开发出来的一个多级
边缘检测算法,其目标是找到一个最优的边缘,其最优边缘的定义是:
1.好的检测 --算法能够尽可能多地标示出图像中的实际边缘
2.好的定位 --标识出的边缘要与实际图像中的实际边缘尽可能接近
3.最小响应 --图像中的边缘只能标识一次,并且可能存在的图像噪声不应该标识为边缘

原理参考:https://www.cnblogs.com/chenzhen0530/p/14690472.html
#include
#include
using namespace std;
using namespace cv;
/**
* 边缘处理
*/
Mat src, srcBlur, srcGray;
const int MAX_THRESHOLD = 255;
int t1_value = 50;
char output_wind[] = "output";
void Canny_Demo(int, void*);
int main() {
// 读取图像
src = imread("C:/Users/Dell/Desktop/images.png");
if (src.empty()) {
cout << "could not load image." << endl;
return -1;
}
namedWindow("src", WINDOW_AUTOSIZE);
imshow("src", src);
GaussianBlur(src, srcBlur, Size(3, 3), 0, 0);
cvtColor(srcBlur, srcGray, COLOR_BGR2GRAY);
namedWindow(output_wind, WINDOW_AUTOSIZE);
createTrackbar("Threshold: ", output_wind, &t1_value, MAX_THRESHOLD, Canny_Demo);
Canny_Demo(0, 0);
waitKey(0);
return 0;
}
void Canny_Demo(int, void*) {
Mat edgeOutput;
Canny(srcGray, edgeOutput, t1_value, t1_value * 2, 3, false);
imshow(output_wind, edgeOutput);
}
4.Adam, AdaGrad的区别
深度学习优化算法经历了 SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam 这样的发展历程。
Adam 对比于AdaGrad就是使用了一阶动量和二阶动量都使用了,而AdaGrad只使用了二阶动量
具体可以参考:https://zhuanlan.zhihu.com/p/32230623
有详细的优化算法发展历程。



