YB菜菜的机器学习自学之路(七)——简单了解keras框架
YB菜菜的机器学习自学之路(七)——简单了解keras框架
- 前提说明
- 1. 机器学习框架-keras
-
- 1.1 keras框架的特点
- 1.2 keras框架实现一个神经元的建立的过程
- 2. 举例说明
-
- 2.1 一个神经元 和输入特征为1的案例
- 2.2 多神经元 和单输入特征为1的案例
- 2.3 多输入,单神经元
- 2.4 多输入多神经元案例
前提说明
一个一个编写前向传播和后向传播是十分麻烦的,一些打包好的机器学习框架可以帮助我们解决这些问题。这里简单了解keras框架,然后记录**课程《小白也能听懂的人工智能课》**中几个简单的应用例子。
1. 机器学习框架-keras
1.1 keras框架的特点
》Keras框架实现了机器学习神经网络底层复杂数学运算的封装,可以通过它提供的上层接口搭建模型。
除了Keras框架外,还有Tensorflow等框架。
》相比于Tensorflow框架,Keras更像是python,其主要特点是简单易用。但不如Tensorflow(更接近C语言)灵活和强大。
1.2 keras框架实现一个神经元的建立的过程
(1)导入keras框架
from keras.models import Sequential
(2)创建模型
model = Sequential()
(3)创建一个神经元
model.add(Dense(uints=, activation='', input_dim = ))
其中
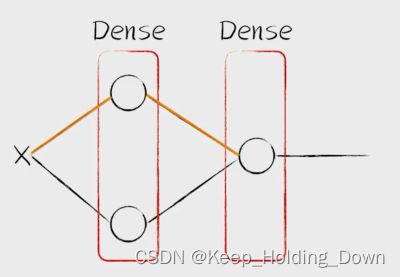
Dense: 设置神经元层数,是一个全链接层
uiits: 设置当前层的神经元数量
activation:设置激活函数类型
input_dim:输入数据特征维度
(4)告诉keras使用什么样的代价函数和调整方法
model.compile(loss='',optimizer='',metrics=[''])
其中:
loss: 设置代价函数
optimizer : 设置优化器,包括学习率等
metrics: 设置评估标准
(5)开始训练
model.fit(x,y,epochs=,batch_size=)
其中
x:观测量中的自变量数据
y: 观测量中的因变量数据
epochs:设置训练回合数
batch_size: 批量数
2. 举例说明
2.1 一个神经元 和输入特征为1的案例
(2)导入keras和层
from keras.models import Sequential
from keras.layers import Dense
(2)设置层
model = Sequential()
model.add(Dense(units=1, activation='sigmoid', input_dim = 1))
Sequential 是堆叠神经元的载体,神经元堆叠在一起形成一个网络预测模型(model)
在这个model内部增加一个全连接层:
uiits=1: 设置当前层的神经元数量为1
activation=‘sigmoid’:设置激活函数类型为sigmoid
input_dim=1:输入数据特征维度,因为数据维度只有1个 所以设置为1
(3)设置代价函数和梯度下降算法
model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.01),metrics=['accuracy'])
loss: 设置代价函数为均方根误差
optimizer : 设置SGD(梯度下降),以及学习率lr为0.01
metrics: 设置精度为评估标准
(4)开始训练
model.fit(X,Y,epochs=5000, batch_size=10)
训练回合为5000
每次使用观测量中的10个数据
(5)针对训练结果查看预测结果
pres = model.predict(X)
2.2 多神经元 和单输入特征为1的案例
from keras.models import Sequential
from keras.layers import Dense
(2)设置层
model = Sequential()
model.add(Dense(units=2, activation='sigmoid', input_dim = 1))
model.add(Dense(units=1, activation='sigmoid'))
与前面不同,这里有3个神经元,共两层
因此需要再增加一个model.add
注:由于Dense是全链接,所以第二个add不需要再写输入维度。
(3)设置代价函数和梯度下降算法
model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy'])
loss: 设置代价函数为均方根误差
optimizer : 设置SGD(梯度下降),以及学习率lr为0.05 (调参)
metrics: 设置精度为评估标准
(4)开始训练
model.fit(X,Y,epochs=5000, batch_size=10)
训练回合为5000
每次使用观测量中的10个数据
(5)针对训练结果查看预测结果
pres = model.predict(X)
2.3 多输入,单神经元
(1)数据导入
(2)导入keras和层
from keras.models import Sequential
from keras.layers import Dense
(2)设置层
model = Sequential()
model.add(Dense(units=1, activation='sigmoid', input_dim = 2))
与前面不同,这里数据有2个维度,所以输入维度设置为2
(3)设置代价函数和梯度下降算法
model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy'])
loss: 设置代价函数为均方根误差
optimizer : 设置SGD(梯度下降),以及学习率lr为0.05 (调参)
metrics: 设置精度为评估标准
(4)开始训练
model.fit(X,Y,epochs=5000, batch_size=10)
训练回合为5000
每次使用观测量中的10个数据
(5)针对训练结果查看预测结果
pres = model.predict(X)
2.4 多输入多神经元案例
(2)设置层
model = Sequential()
model.add(Dense(units=2, activation='sigmoid', input_dim = 2))
model.add(Dense(units=1, activation='sigmoid'))
这里有3个神经元,共两层,且2个输入
因此需要再增加一个model.add
注:由于Dense是全链接,所以第二个add不需要再写输入维度。
(3)设置代价函数和梯度下降算法
model.compile(loss='mean_squared_error',optimizer=SGD(lr=0.05),metrics=['accuracy'])
loss: 设置代价函数为均方根误差
optimizer : 设置SGD(梯度下降),以及学习率lr为0.05 (调参)
metrics: 设置精度为评估标准
(4)开始训练
model.fit(X,Y,epochs=5000, batch_size=10)
训练回合为5000
每次使用观测量中的10个数据
(5)针对训练结果查看预测结果
pres = model.predict(X)







