“深度学习”学习日记。卷积神经网络--用CNN的实现MINIST识别任务
2023.2.11
通过已经实现的卷积层和池化层,搭建CNN去实现MNIST数据集的识别任务;
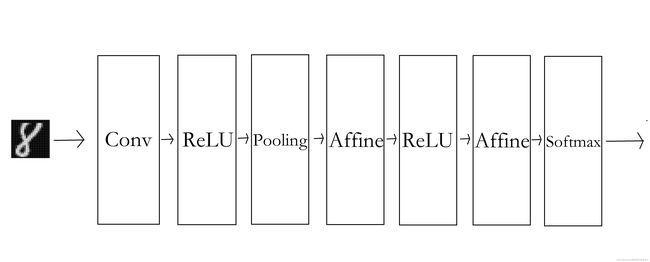
一,简单CNN的网络构成:
代码需要在有网络的情况下运行,因为会下载MINIST数据集,运行后会生成params.pkl保留训练权重;
简单卷积层的基本参数:
"""简单的ConvNet conv - relu - pool - affine - relu - affine - softmax Parameters ---------- input_size : 输入大小(MNIST的情况下为784) hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100]) output_size : 输出大小(MNIST的情况下为10) activation : 'relu' or 'sigmoid' weight_init_std : 指定权重的标准差(e.g. 0.01) 指定'relu'或'he'的情况下设定“He的初始值” 指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值” """一开始时,这里的超参数通过命名为conv_param的字典传入,他会像{'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},这样,保存必要的超参数。
在初始化权重前,这里将由初始化参数传入卷积层的超参数从字典中取出,然后计算卷积层的输出大小,再进行参数初始化
在生成层,学习所需要的参数是第一层卷积层和剩余两个全连接层的权值和偏置,将这些参数保存在实例变量的字典中,将第一层卷积层的权重设为w1,偏置设为b1。
在全连接层,从前面开始按顺序像有序字典(Orderdict)的Layers中添加层。只有最后的SoftmaxWithLoss层被添加到变得变量lastlayers。
以上就是简单卷积神经网络(SimpleConvnet)的初始化中进行的处理。像这样初始化,进行推理处理和求损失函数loss
用误差反向传播法传递参数的梯度,最后把各个权重参数的梯度保存到grads字典中,通过正向传播和反向传播组装在一起,完成简单卷积神经网络的实现;
简单卷积层的代码:
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
#全连接层
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
"""求梯度(数值微分)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
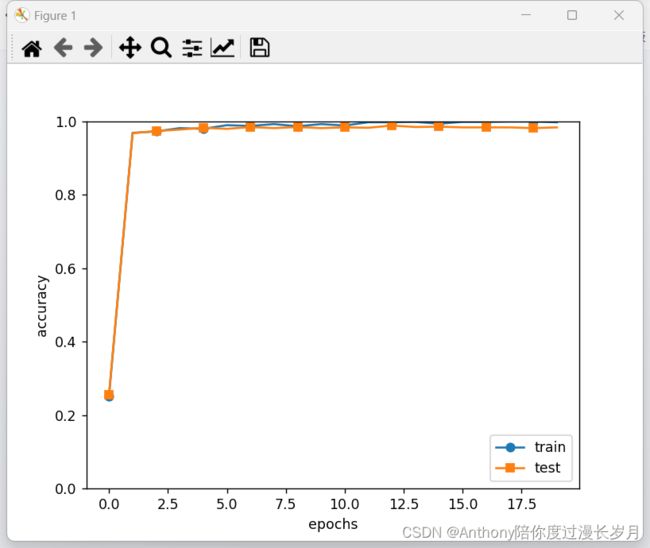
实验正确率对比:
使用MINIST数据集训练SimpleConvnet,可以对比以前文章没有使用“卷积”神经网络的MINIST识别任务的正确率:这是一个一步步完善的过程
“深度学习”学习日记。神经网络的推理处理_Anthony陪你度过漫长岁月的博客-CSDN博客
“深度学习”学习日记。神经网络的学习。--学习算法的实现_Anthony陪你度过漫长岁月的博客-CSDN博客
“深度学习”学习日记。误差反向传播法--算法实现_Anthony陪你度过漫长岁月的博客-CSDN博客
卷积神经网络可以有效的读取图像的某种特征而调整参数权重,测试集的识别率为:0.987,对于小型神经网络这个正确率不错了,接下来通过叠加层来加深神经网络,提高正确率。
实验代码1:
可以减少测试数据节省时间:同时也会降低正确率
# 读入数据 (x_train, t_train), (x_test, t_test) = load_mnist(flatten=False) # 处理花费时间较长的情况下减少数据 # x_train, t_train = x_train[:5000], t_train[:5000] # x_test, t_test = x_test[:1000], t_test[:1000]
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
from collections import OrderedDict
import matplotlib.pyplot as plt
try:
import urllib.request
except ImportError:
raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np
url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
'train_img': 'train-images-idx3-ubyte.gz',
'train_label': 'train-labels-idx1-ubyte.gz',
'test_img': 't10k-images-idx3-ubyte.gz',
'test_label': 't10k-labels-idx1-ubyte.gz'
}
dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"
train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784
def _download(file_name):
file_path = dataset_dir + "/" + file_name
if os.path.exists(file_path):
return
print("Downloading " + file_name + " ... ")
urllib.request.urlretrieve(url_base + file_name, file_path)
print("Done")
def download_mnist():
for v in key_file.values():
_download(v)
def _load_label(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
labels = np.frombuffer(f.read(), np.uint8, offset=8)
print("Done")
return labels
def _load_img(file_name):
file_path = dataset_dir + "/" + file_name
print("Converting " + file_name + " to NumPy Array ...")
with gzip.open(file_path, 'rb') as f:
data = np.frombuffer(f.read(), np.uint8, offset=16)
data = data.reshape(-1, img_size)
print("Done")
return data
def _convert_numpy():
dataset = {}
dataset['train_img'] = _load_img(key_file['train_img'])
dataset['train_label'] = _load_label(key_file['train_label'])
dataset['test_img'] = _load_img(key_file['test_img'])
dataset['test_label'] = _load_label(key_file['test_label'])
return dataset
def init_mnist():
download_mnist()
dataset = _convert_numpy()
print("Creating pickle file ...")
with open(save_file, 'wb') as f:
pickle.dump(dataset, f, -1)
print("Done!")
def _change_one_hot_label(X):
T = np.zeros((X.size, 10))
for idx, row in enumerate(T):
row[X[idx]] = 1
return T
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
if not os.path.exists(save_file):
init_mnist()
with open(save_file, 'rb') as f:
dataset = pickle.load(f)
if normalize:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].astype(np.float32)
dataset[key] /= 255.0
if one_hot_label:
dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
if not flatten:
for key in ('train_img', 'test_img'):
dataset[key] = dataset[key].reshape(-1, 1, 28, 28)
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
if __name__ == '__main__':
init_mnist()
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
class Nesterov:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
self.dW = None
self.db = None
def forward(self, x):
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size:
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
return col
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_shape
out_h = (H + 2 * pad - filter_h) // stride + 1
out_w = (W + 2 * pad - filter_w) // stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
self.x = None
self.col = None
self.col_W = None
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h * self.pool_w)
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1: t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i * batch_size:(i + 1) * batch_size]
tt = t[i * batch_size:(i + 1) * batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i + 1)]
self.layers[key].b = self.params['b' + str(i + 1)]
class Trainer:
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr': 0.01},
evaluate_sample_num_per_epoch=None, verbose=True):
self.network = network
self.verbose = verbose
self.x_train = x_train
self.t_train = t_train
self.x_test = x_test
self.t_test = t_test
self.epochs = epochs
self.batch_size = mini_batch_size
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
optimizer_class_dict = {'sgd': SGD, 'momentum': Momentum, 'nesterov': Nesterov,
'adagrad': AdaGrad, 'rmsprpo': RMSprop, 'adam': Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)
self.train_size = x_train.shape[0]
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
self.max_iter = int(epochs * self.iter_per_epoch)
self.current_iter = 0
self.current_epoch = 0
self.train_loss_list = []
self.train_acc_list = []
self.test_acc_list = []
def train_step(self):
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
grads = self.network.gradient(x_batch, t_batch)
self.optimizer.update(self.network.params, grads)
loss = self.network.loss(x_batch, t_batch)
self.train_loss_list.append(loss)
if self.verbose: print("train loss:" + str(loss))
if self.current_iter % self.iter_per_epoch == 0:
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print(
"=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(
test_acc) + " ===")
self.current_iter += 1
def train(self):
for i in range(self.max_iter):
self.train_step()
test_acc = self.network.accuracy(self.x_test, self.t_test)
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 处理花费时间较长的情况下减少数据
x_train, t_train = x_train[:5000], t_train[:5000]
x_test, t_test = x_test[:1000], t_test[:1000]
max_epochs = 20
network = SimpleConvNet(input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
network.save_params("params.pkl")
print("Saved Network Parameters!")
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
二,CNN的可视化:
通过卷积层的可视化,来学习卷积层到底卷积了什么?(如何处理?)
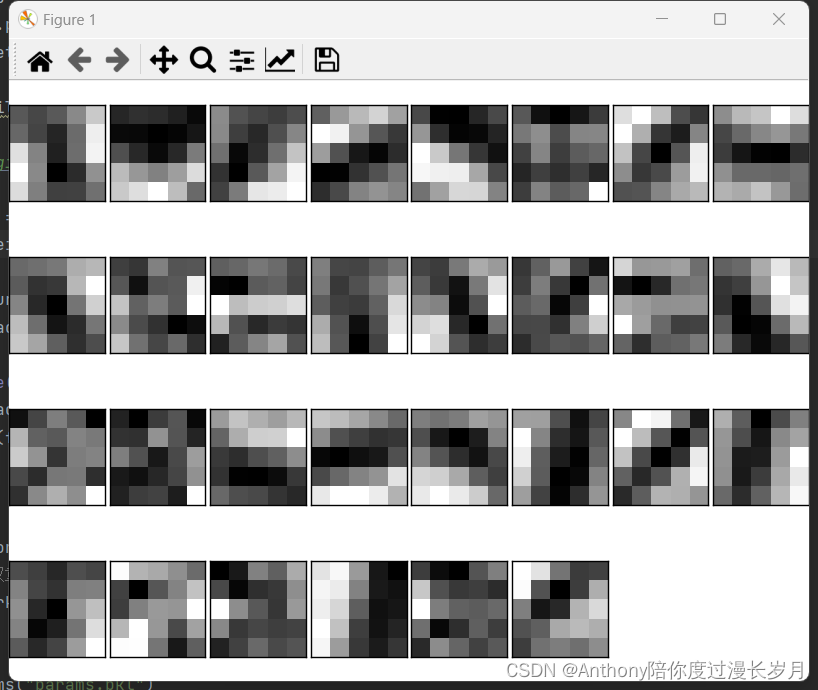
1,第一层权重的可视化:
在简单卷积层的一个权重参数, conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},中可以知道学习前的权重是(30,1,5,5),这意味着卷积核的大小是5X5、通道数为1,表示卷积核可以可视化为1通道的灰色图像;
“cnn可视化”,实验代码2:写在实验代码1的末尾:
def filter_show(filters, nx=8, margin=3, scale=10):
FN, C, FH, FW = filters.shape
ny = int(np.ceil(FN / nx))
fig = plt.figure()
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(FN):
ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
network = SimpleConvNet()
# 随机进行初始化后的权重
filter_show(network.params['W1'])
# 学习后的权重
network.load_params("params.pkl")
filter_show(network.params['W1'])运行结果:学习前的卷积核随机初始化,这样的图像在黑白分布上没有规律可以寻找;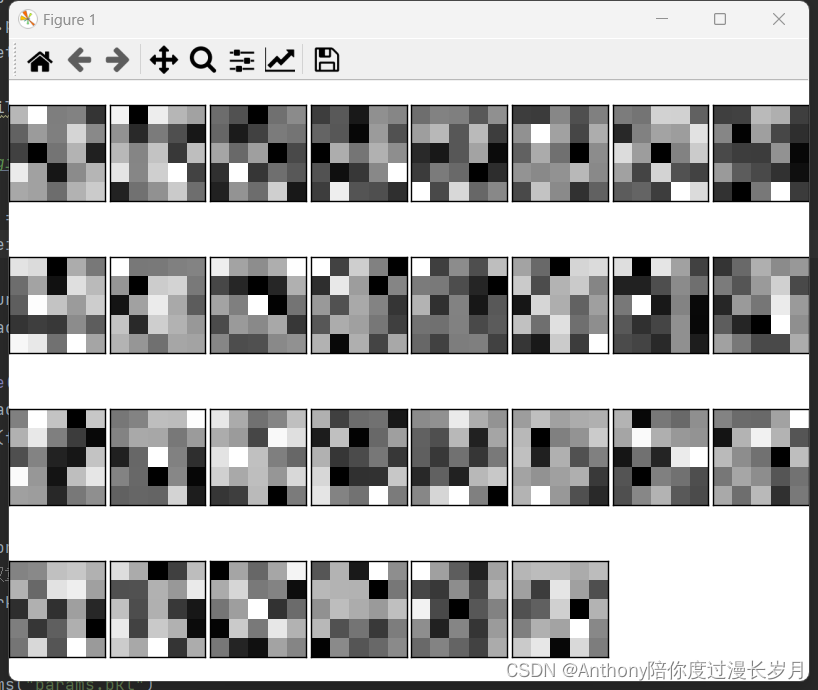
学习后,卷积核被更新成了有规律的图像,含有块状区域(blob)
学习前和学习后,虽然权重元素都是实数,但是,在图像的显示上,统一将最小值显示称为黑色,最大值为白色;这好像卷积核在观察着什么东西观察边沿(颜色变化的分界线)和斑块(局部的块状区域)等,现在就研究一下这个问题。
实验代码:写在实验代码1的末尾:
注意图片的输入路径:
代码来源于教材,作者能力问题,无法使用任意图片进行实验,会附上教材的图片。
2023.2.11
命名为lena_gray。
def filter_show(filters, nx=4, show_num=16):
FN, C, FH, FW = filters.shape
ny = int(np.ceil(show_num / nx))
fig = plt.figure()
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(show_num):
ax = fig.add_subplot(4, 4, i + 1, xticks=[], yticks=[])
ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
network = SimpleConvNet(input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
# 学习后的权重
network.load_params("params.pkl")
filter_show(network.params['W1'], 16)
img = imread('../dataset/lena_gray.png')
img = img.reshape(1, 1, *img.shape)
fig = plt.figure()
w_idx = 1
for i in range(16):
w = network.params['W1'][i]
b = 0 # network.params['b1'][i]
w = w.reshape(1, *w.shape)
# b = b.reshape(1, *b.shape)
conv_layer = Convolution(w, b)
out = conv_layer.forward(img)
out = out.reshape(out.shape[2], out.shape[3])
ax = fig.add_subplot(4, 4, i + 1, xticks=[], yticks=[])
ax.imshow(out, cmap=plt.cm.gray_r, interpolation='nearest')
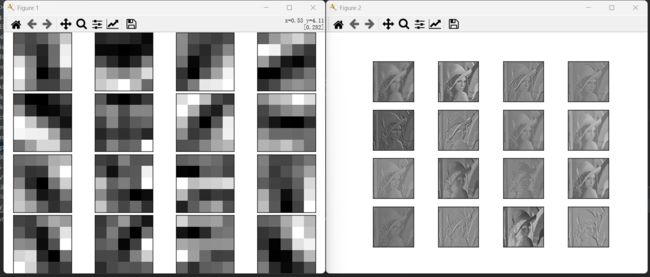
plt.show()观察实验结果:
可以观察到figure1对水平方向上的边缘有反应的卷积核:在figure2垂直方向的边缘上有白色像素;figure2对垂直方向上的边缘有反应的卷积核:在figure2水平方向的边缘上有白色像素;
由此得知,卷积层的卷积核会提取边缘或斑块等的原始信息,而刚才是实现的CNN会将这些原始信息传递给后面的层。
2,基于分层结构的信息提取:
像边缘、斑块这样的信息称为低级信息,在只有一层卷积层的CNN被提取,如果在叠加了多层的CNN中,各层中优惠提取什么样的信息呢?
根据深度学习的可视化相关研究,随着层次的加深,提取的信息(反应强烈的神经元)也会缘来缘抽象。最开始是对简单的边缘有相应,接下来的层对纹理有反应,再后面的层会对更加复杂的物体部件有反应。也就是说,随着层次的加深,神经元从简单的形状向“高级”信息变化
三、具有代表性的CNN:
迄今为止,已经提出了各种网络结构。有两个网络非常具有代表性;
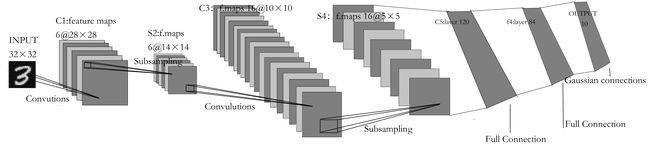
1,LeNet:
LeNet在1988年首次被提出,用于完成MNIST识别任务。
特点:
1,“抽选元素”的子采样层(也是跟CNN一样的连续的卷积层和池化层);
2,LeNet的激活函数使用sigmoid函数,而现在的CNN使用ReLU函数;
3.原始的LeNet中使用子采样(subsampling)缩小空间中的各个数据的大小,而现在的CNN中Max池化是主流操作;
LeNet结构图:
2,AlexNet:
AlexNet是引发深度学习热潮的导火线,他的结构与LeNet基本上没有区别,AlexNet叠有多个卷积层和池化层,最后由全连接层输出结果。
特点:
1,激活函数使用ReLU函数;
2,使用进行局部正规化的LRN(Local Response Noramlization)
3,使用Droput
关于Droput可以参考:“深度学习”学习日记。与学习有关的技巧--正则化_Anthony陪你度过漫长岁月的博客-CSDN博客权值衰减,https://blog.csdn.net/m0_72675651/article/details/128786693
大多数情况下深度学习(加深层次)的网络存在大量参数。因此,学习需要大量的计算,并且需要时那些参数“配对”的大量数据。现在大多数人都可以获得大量的数据和高性能GPU的普及,他们成为深度学习发展的原动力