ARIMA模型实例讲解:时间序列预测需要多少历史数据?
时间序列预测,究竟需要多少历史数据?
显然,这个问题并没有一个固定的答案,而是会根据特定的问题而改变。
在本教程中,我们将基于 Python 语言,对模型输入大小不同的历史数据,对时间序列预测问题展开讨论,探究历史数据对 ARIMA 预测模型的性能影响。(雷锋网(公众号:雷锋网)注:ARIMA 全程是 Autoregressive Integrated Moving Average Model,即自回归积分滑动平均模型)
具体来说,在本教程中,我们将:
● 加载标准数据集并输入 ARIMA 模型;
● 对历史数据年份进行敏感性分析;
● 分析敏感性分析的结果。
通过本例提供的模板,大家将可以根据各自特定的时间序列预测场景,展开类似的针对历史数据大小的敏感性分析。
加载数据集
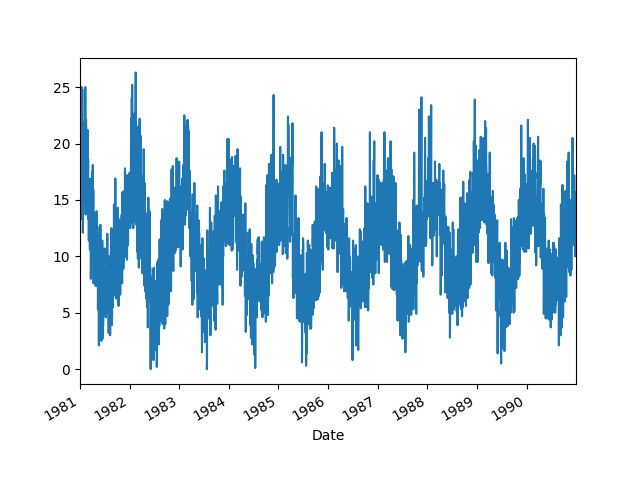
本例中我们使用来自澳大利亚气象局的一份数据,该数据描述了墨尔本市 10 年(1981 - 1990年)内的每日最低气温,单位为摄氏度,观测值共 3650 次。
这里我们将下载好的数据集保存在 daily-minimum-temperature.csv 文件中。
这里需要注意的是,下载文件中有一些多余的“?”字符,可以通过文本编辑器打开并删除,否则模型无法处理。此外,文件中的脚注信息也需要删除。
以下代码展示了如何加载数据库,并生成 Pandas 库中的 Series 对象。
# line plot of time series from pandas import Series from matplotlib import pyplot # load dataset series = Series.from_csv('daily-minimum-temperatures.csv', header=0) # display first few rows print(series.head(20)) # line plot of dataset series.plot() pyplot.show()
运行代码后打印得到的前 20 行数据如下所示:
根据载入数据,可以得到如下图所示的温度变化曲线,从图头中可以看到明显的季节性变化。
搭建 ARIMA 预测模型
在本节中,我们将基于以上数据搭建一个 ARIMA 预测模型。
这里我们不会调整模型参数。而且,为了对数据平稳化并适配 ARIMA 模型,必须先删除数据中包含的明显的季节性变化趋势。
以下代码中,我们通过减去前一年数据的办法来获得数据的季节性差异。需要说明的是,这种方法是很粗糙的,因为它并没有考虑闰年的因素。而且,这也意味着第一年的数据将无法用于建模,因为第一年并没有更早的数据。
# seasonal difference differenced = series.diff(365) # trim off the first year of empty data differenced = series[365:]
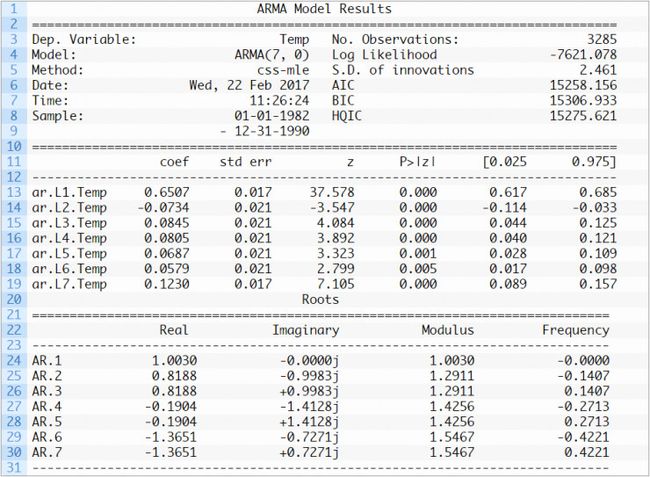
接下来,我们将数据导入 ARIMA(7,0,0) 模型,并打印输出汇总信息。
# fit model model = ARIMA(differenced, order=(7,0,0)) model_fit = model.fit(trend='nc', disp=0) print(model_fit.summary())
打印输出的汇总信息如下:
历史数据的敏感性分析
这一节我们将讨论历史数据大小对模型预测性能的影响。
上文提到,我们原本有 10 年的原始数据,但是由于季节性差异处理,因此只有 9 年的实际数据可用。为了进行历史数据大小的敏感性分析,这里我们将最后一年的数据作为测试样本,依次选择1年、2年一直到8年的剩余数据为训练样本,步进地进行测试,并逐日记录测试情况。根据记录数据,我们还计算了均方根误差(RMSE)来明确反应模型的性能表现。
下面这行代码将经过季节性调整的数据分为训练数据和测试数据。
train, test = differenced[differenced.index < '1990'], differenced['1990']
需要注意的是,这里根据自己的问题预测规模,选择合适的间隔很重要。本例中我们未来对历史数据量进行敏感性分析进行了步进操作。另外,鉴于数据的季节性,本例中一年是数据集的最好的时间间隔。但感兴趣的朋友根据问题域的变化也可以选择其他间隔,例如阅读或者多年时间间隔。
以下是具体代码:
# split train, test = differenced[differenced.index < '1990'], differenced['1990'] years = ['1989', '1988', '1987', '1986', '1985', '1984', '1983', '1982'] for year in years: # select data from 'year' cumulative to 1989 dataset = train[train.index >= year]
定好了数据之后,下一步是评估 ARIMA 模型。
具体的步进评估方法是:首先选取一个时间段的数据,并根据选定数据建模,训练,然后对下一段数据进行预测,预测后记录数据并计算正确率。接着,将真实的观察数据加入建模数据,建立新的模型并展开训练,对再下一段数据进行预测,并记录结果。依次进行,知道数据用完。
最终,预测结果将被集合在一起,与真实观察数据中的最后一年比较,计算出错误情况。在这种情况下,RMSE 将被用作预测得分,并将与观察结果的数量级等同。
具体代码如下:
# walk forward over time steps in test values = dataset.values history = [values[i] for i in range(len(values))] predictions = list() test_values = test.values for t in range(len(test_values)): # fit model model = ARIMA(history, order=(7,0,0)) model_fit = model.fit(trend='nc', disp=0) # make prediction yhat = model_fit.forecast()[0] predictions.append(yhat) history.append(test_values[t]) rmse = sqrt(mean_squared_error(test_values, predictions)) print('%s-%s (%d values) RMSE: %.3f' % (years[0], year, len(values), rmse))
运行代码后的打印输出结果如下。需要注意的是,因为代码在每个历史训练数据间隔都创建了 356 个 ARIMA 模型,因此可能需要一些时间。
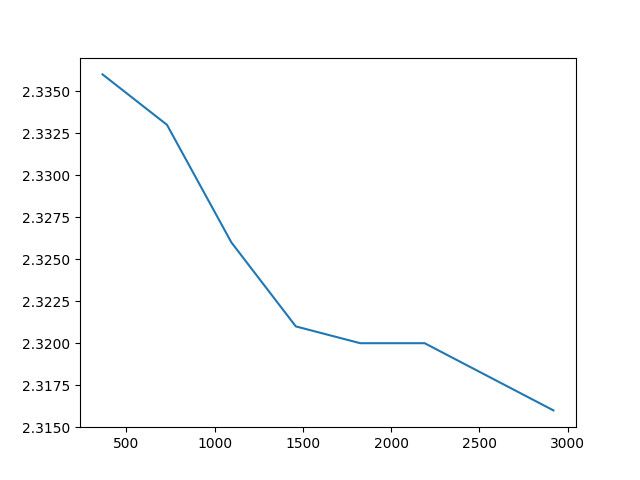
1989-1989 (365 values) RMSE: 2.336 1989-1988 (730 values) RMSE: 2.333 1989-1987 (1095 values) RMSE: 2.326 1989-1986 (1460 values) RMSE: 2.321 1989-1985 (1825 values) RMSE: 2.320 1989-1984 (2190 values) RMSE: 2.320 1989-1983 (2555 values) RMSE: 2.318 1989-1982 (2920 values) RMSE: 2.316
从结果可以看到,随着可用历史数据的增多,模型的误差总体呈下降趋势。
但同时也应该看到,在 4-5 年的时间段,不断增长历史数据的效果收益率实际上是递减的。也就是说,在历史数据不足或模型训练时间无法满足要求时,也可以根据实际需求,利用相对较少的历史数据,得到一个性价比最高的结果。
以下代码是根据测试数据绘制曲线图的过程。
from matplotlib import pyplot x = [365, 730, 1095, 1460, 1825, 2190, 2555, 2920] y = [2.336, 2.333, 2.326, 2.321, 2.320, 2.320, 2.318, 2.316] pyplot.plot(x, y) pyplot.show()
运行后得到的曲线如图所示。
从曲线图可以更清晰地看到总体上历史数据越多,预测结果就更精确这一变化趋势。因为历史数据越多,就意味着系数的优化越精确,符合数据变化的内在规律的可能性就越高。
但同时也可以从上图中看到另一个现象:大多数时候人们觉得历史数据越多,模型的表现就越好。但实际上,连续两年或三年的数据之间并没有什么根本性的差别,因此灵活选择时间跨度也至关重要。
局限性和扩展
我们通过本次教程为大家演示了如何设计、执行和分析基于时间序列预测的历史数据敏感性分析。现针对样例中的一些局限和可能的扩展项目整理如下:
1. 模型参数未调试。本例中我们使用的 ARIMA 模型并未针对问题域进行过任何的参数调节。在理想状态下,一个针对历史数据量的敏感性分析应该基于一个经过参数调节的 ARIMA 模型。
2. 统计学意义。上文中提到的,针对不同的历史数据,模型的不同预测表现是否具有统计学意义,目前尚不清楚。但 Pairwise 统计学显着性检验可用于评估 RMSE 的差异是否有意义。
3. 其他模型。本例中我们使用了 ARIMA 模型来进行历史数据的系数拟合。感兴趣的朋友可以换用其他模型进行类似的研究,各个模型对历史数据的敏感性和处理方式也各不相同。
4. 其他时间间隔。本例中我们以一年为时间间隔,但实际上也可以选择其他间隔。例如几个星期、几个月或者几年,要根据不同的问题域灵活选择。另外,如上文所述,还要考虑相邻时间段之间数据的相似性,这也是一个很重要的影响因素。