模式识别和机器学习实战- 集成学习- Python实现 - AdaBoost算法
文章目录
- 前言
- 一、AdaBoost算法
-
- 原理概述
- 二、实战基于单层决策树构建弱分类器
-
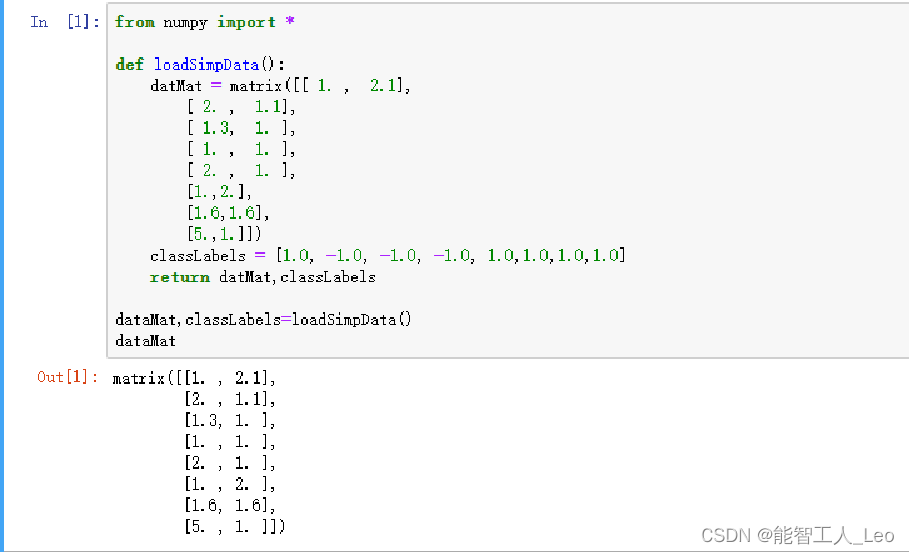
- 1. 简单数据集构建
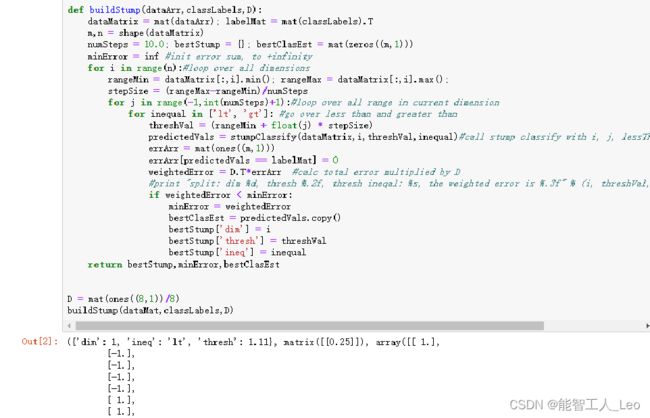
- 2. 建立单层决策树
- 三、完整AdaBoost实现以及测试算法
- 附加题:实战之房价预测
- 完整代码
前言
我们在思考一个问题的时候,往往会考虑多个意见而不会只听一家之言,集成学习正是基于这种想法发展来的。事实上,集成学习是对其它算法进行组合的一种方式。
集成学习算法分类:bagging && boosting
bagging:基于数据随机重抽样的分类器(自举汇聚法),是在原始数据集选择S次获得S个新数据集(可重复)的技术,将某个分类算法作用于S个数据集得到S个分类器,最后选择投票结果最多的类别用作结果。
boosting:通过改变数据分布来实现的,它根据每次训练集之中每个样本的分类是否正确,以及上次的总体分类的准确率,来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练,最后将每次训练得到的分类器最后融合起来,作为最后的决策分类器
而其中AdaBoost是boosting最流行的版本,是最好的监督学习方法,机器学习强有力工具之一
本文具体的文件和代码,在如下链接里:[Adaboost数据集和源码](https://download.csdn.net/download/LeoEdwin/85078817)
一、AdaBoost算法
原理概述
Adaboost 算法原理 作为集成学习的一种算法,根据“好而不同”的原则,将多个弱分类器,组合成强分类 器。每个分类器的不同是通过改变样本数据分布来实现的,根据每次训练集之中每个样本的 分类是否正确,以及上次的总体分类的准确率,来确定每个样本的权值。将修改过权值的新 数据集送给下层分类器进行训练,最后将每次训练得到的分类器最后融合起来,作为最后的 决策分类器。
使用弱分类器构建一个强分类器时,这里的“弱”指比随机好(分类正确率至少比50%高),但又没好太多。
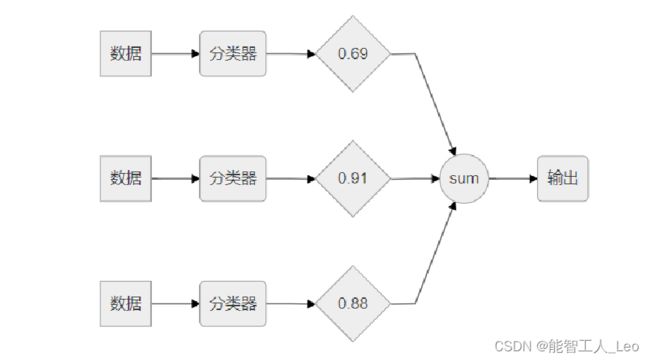
基本步骤:
训练数据中每个样本,赋予一个权重,这些权重构成向量D,初始是相同值。
首先在训练数据上训练一个弱分类器并计算错误率,然后统一数据集上再次训练弱分类器,第二次训练时调整每个样本的权重,第一次分对的样本权重会变低,分错的变高,具体计算如下:
错误率ε=未正确分类的样本数目/所有样本数目
权重值α=1/2ln(1−ε/ε)
如果分对权重D更改为:D_i^(t+1)= D_i(t)e−α/Sum(D)
如果分错权重D更改为:D_i^(t+1)= D_i(t)eα/Sum(D)
重复迭代训练调整权重,直到训练错误率为0或者达到用户指定值为止

二、实战基于单层决策树构建弱分类器
1. 简单数据集构建
2. 建立单层决策树

代码解释:三层for循环调用stumpClassify函数,函数返回分类预测结果。
构建向量errArr,弱predictedVals值不等于真正类别标签,那么errArr对应位置1,将错误向量和权重向量D相应元素相乘求和得到weightedError,使用bestStump字典保存单层决策树用于返回给AdaBoost算法
三、完整AdaBoost实现以及测试算法
输入为数据集 dataArr、标签集 classLabels,以及训练轮次 numlt,最后错误率达到 0 会 提前结束训练;先 for 循环共计 40 次,每轮用决策树分类,用该分类器的错误率计算权重, 并且更新样本的权重分布 D;结束后返回 weakClassArr 为每个决策树的路径记录向量

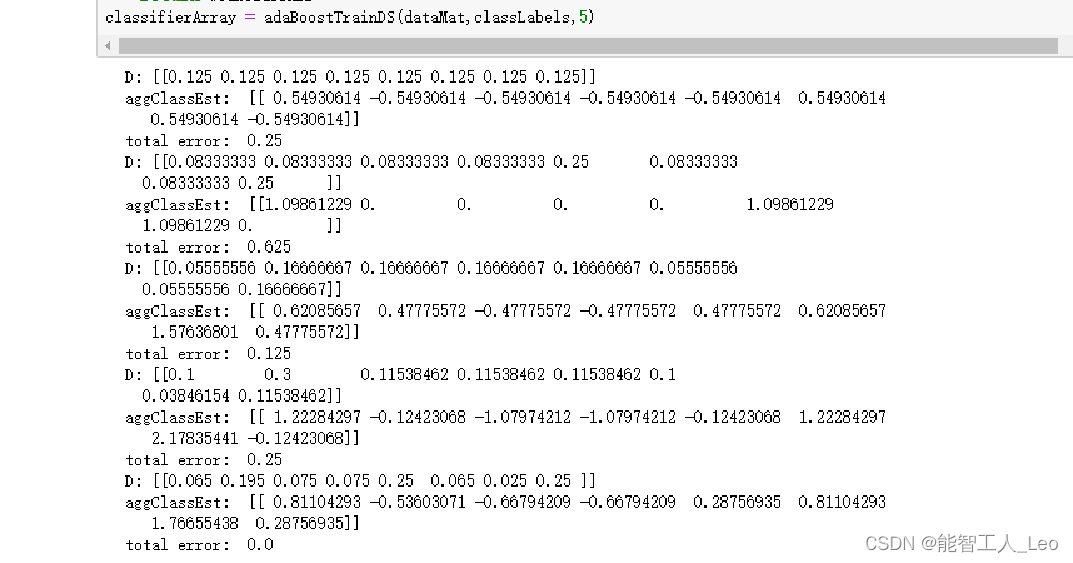
新样本的测试:输入测试集和由集成学习得到的强分类器;用 classEst 记录每一个分类器的结果, aggClassEst 为每个分类器乘上权重后的和,最后返回 sign(aggClassEst)
附加题:实战之房价预测
难数据集:样本数据为高维数据时;
在之前代码的基础上修改载入数据的函数,其他部分不变
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
def loadDataSet(fileName):
fr = open(fileName, "r")
dataMat = []
labelMat = []
numFeat = len(fr.readline().split("\t"))
for line in fr.readlines():
lineArr = []
curLine = line.strip().split("\t")
for i in range(numFeat - 1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
fr.close()
return dataMat, labelMat
房价数据集 kc_house_data.csv
本实验主要是依据房屋的属性信息,包括房屋的卧室数量,卫生间数量,房屋的大小,房屋地下室的大小,房屋的外观,房屋的评分,房屋的修建时间,房屋的翻修时间,房屋的位置信息等,对房屋的价格进行预测,从而为此类价格类实际问题的处理提供技术参考。
这里使用 sklearn 库,并使用了线性回归和回归树计算,以及分别使用 Adaboost 进行计算相比较
from matplotlib import pyplot as plt
from sklearn import neighbors
from sklearn import ensemble
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import csv
import numpy
fp = open('kc_house_data.csv')
fp_data = csv.reader(fp)
y = []
x = []
for line in fp_data:
if line[0] != 'id':
line[1] = line[1][0:8]
y.append(float(line[2]))
line.remove(line[2])
li = []
for i in line:
li.append(float(i))
x.append(li)
x = numpy.array(x)
y = numpy.array(y)
fp.close()
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 训练集与测试集之比
#adaboost算法(线性回归作为弱学习器)
adaboost = AdaBoostRegressor(LinearRegression())
adaboost.fit(x_train, y_train)
y_pre1 = adaboost.predict(x_test)
print("adaboost训练集分数:",adaboost.score(x_train,y_train))
print("adaboost验证集分数:",adaboost.score(x_test,y_test))
print('Adaboost算法(线性回归作为弱分类器)误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre1))
#线性回归作为学习器
Linear = LinearRegression()
Linear.fit(x_train, y_train)
y_pre2 = Linear.predict(x_test)
print("单个线性回归训练集分数:",Linear.score(x_train,y_train))
print("单个线性回归验证集分数:",Linear.score(x_test,y_test))
print('线性回归算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre2))
#adaboost算法(回归树作为弱学习器)
adaboost = AdaBoostRegressor(DecisionTreeRegressor())
adaboost.fit(x_train, y_train)
y_pre3 = adaboost.predict(x_test)
print('Adaboost算法(回归树)误差:')
print("adaboost回归树训练集分数:",adaboost.score(x_train,y_train))
print("adaboost回归树验证集分数:",adaboost.score(x_test,y_test))
print(mean_squared_error(y_true=y_test, y_pred=y_pre3))
#普通回归树作为学习器
decision_tree = DecisionTreeRegressor()
decision_tree.fit(x_train, y_train)
y_pre4 = decision_tree.predict(x_test)
print("普通回归树训练集分数:",decision_tree.score(x_train,y_train))
print("普通回归树验证集分数:",decision_tree.score(x_test,y_test))
print('普通回归树算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre4))
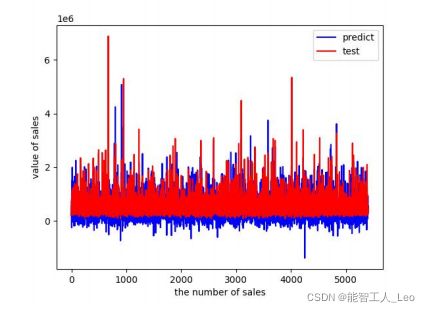
# 做ROC曲线
plt.figure()
plt.plot(range(len(y_pre1)), y_pre1, 'b', label="predict")
plt.plot(range(len(y_pre1)), y_test, 'r', label="test")
plt.legend(loc="upper right") # 显示图中的标签
plt.xlabel("the number of sales")
plt.ylabel('value of sales')
plt.show()
# KNN算法
adaboost = AdaBoostRegressor(neighbors.KNeighborsRegressor())
adaboost.fit(x_train, y_train)
y_pre5 = adaboost.predict(x_test)
print('Adaboost算法(KNN作为弱分类器)误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre5))
KN = neighbors.KNeighborsRegressor()
KN.fit(x_train, y_train)
y_pre5 = KN.predict(x_test)
print('KNN算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre5))
运行结果

可见,使用回归树时的集成学习算法的误差较小; 而线性回归表现则相反。
完整代码
1.基于单层决策树构建弱分类器
from numpy import *
def loadSimpData(): # 导入数据
datMat = matrix([[1., 2.1],
[2., 1.1],
[1.3, 1.],
[1., 1.],
[2., 1.],
[1., 2.],
[1.6, 1.6],
[5., 1.]])
classLabels = [1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0]
return datMat, classLabels
def stumpClassify(dataMatrix, dimen, threshVal, threshIneq): # 单层的决策树
retArray = ones((shape(dataMatrix)[0], 1))
if threshIneq == 'lt':
retArray[dataMatrix[:, dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:, dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr, classLabels, D):
dataMatrix = mat(dataArr) # 创建矩阵
labelMat = mat(classLabels).T # 转置
m, n = shape(dataMatrix) # 获得矩阵的长宽
numSteps = 10.0
bestStump = {} # 创建一个字典,存储最佳结果
bestClasEst = mat(zeros((m, 1)))
minError = inf # 初始为无穷大
for i in range(n): # 遍历所有的列向量
rangeMin = dataMatrix[:, i].min()
rangeMax = dataMatrix[:, i].max()
stepSize = (rangeMax - rangeMin) / numSteps
for j in range(-1, int(numSteps) + 1): # 遍历当前方向
for inequal in ['lt', 'gt']: # 大于阈值和小于阈值
threshVal = (rangeMin + float(j) * stepSize) # 阈值
predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal) # 用单层决策树判断
errArr = mat(ones((m, 1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T * errArr # 将错误向量乘上样本权重D
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump, minError, bestClasEst
def adaBoostTrainDS(dataArr, classLabels, numIt=40): # 训练过程
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m, 1)) / m) # init D to all equal
aggClassEst = mat(zeros((m, 1)))
for i in range(numIt):
bestStump, error, classEst = buildStump(dataArr, classLabels, D) # build Stump
print("D:", D.T)
alpha = float(
0.5 * log((1.0 - error) / max(error, 1e-16))) # calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) # store Stump Params in Array
# print "classEst: ",classEst.T
expon = multiply(-1 * alpha * mat(classLabels).T, classEst) # exponent for D calc, getting messy
D = multiply(D, exp(expon)) # Calc New D for next iteration
D = D / D.sum()
# calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha * classEst
print("aggClassEst: ", aggClassEst.T)
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m, 1)))
errorRate = aggErrors.sum() / m
print("total error: ", errorRate)
if errorRate == 0.0: break
return weakClassArr
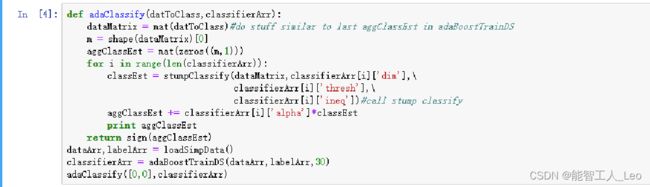
def adaClassify(datToClass, classifierArr):
dataMatrix = mat(datToClass) # do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m, 1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'],
classifierArr[i]['thresh'],
classifierArr[i]['ineq']) # call stump classify
aggClassEst += classifierArr[i]['alpha'] * classEst
print(aggClassEst)
return sign(aggClassEst)
dataArr, labelArr = loadSimpData()
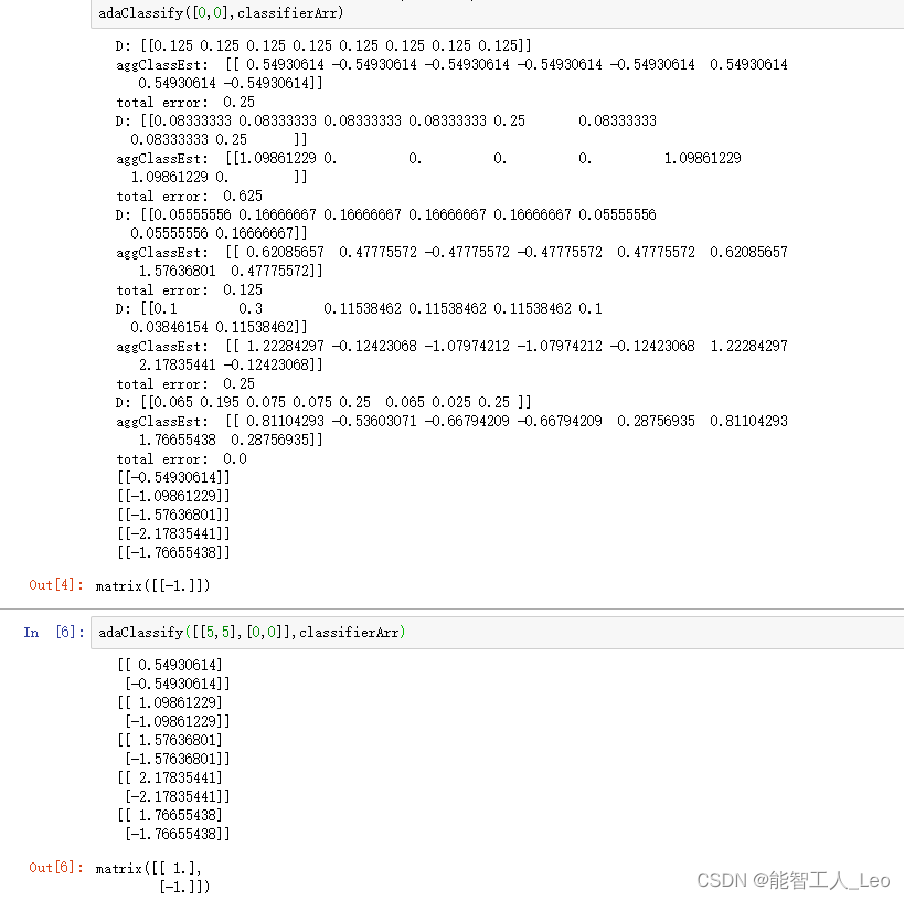
classifierArr = adaBoostTrainDS(dataArr, labelArr, 30)
output1 = adaClassify([3, 6], classifierArr)
print("[3, 6]的分类结果为:", output1)
output2 = adaClassify([0, 0.5], classifierArr)
print("[0, 0.5]的分类结果为:", output2)
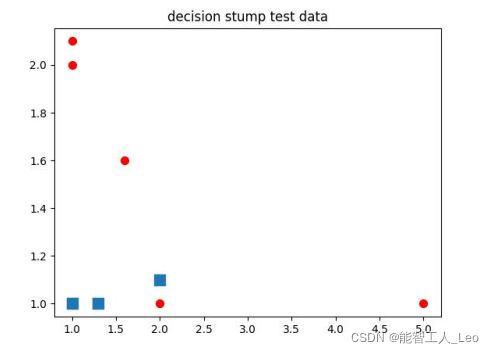
def draw(datMat, classLabels):#可视化
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
markers = []
colors = []
for i in range(len(classLabels)):
if classLabels[i] == 1.0:
xcord1.append(datMat[i, 0]), ycord1.append(datMat[i, 1])
else:
xcord0.append(datMat[i, 0]), ycord0.append(datMat[i, 1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord0, ycord0, marker='s', s=90)
ax.scatter(xcord1, ycord1, marker='o', s=50, c='red')
plt.title('decision stump test data')
plt.show()
draw(dataArr, labelArr)
2.难数据集
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
def loadDataSet(fileName):
fr = open(fileName, "r")
dataMat = []
labelMat = []
numFeat = len(fr.readline().split("\t"))
for line in fr.readlines():
lineArr = []
curLine = line.strip().split("\t")
for i in range(numFeat - 1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
fr.close()
return dataMat, labelMat
def stumpClassify(dataMatrix, dimen, threshVal, threshIneq): # 单层的决策树
retArray = ones((shape(dataMatrix)[0], 1))
if threshIneq == 'lt':
retArray[dataMatrix[:, dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:, dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr, classLabels, D):
dataMatrix = mat(dataArr) # 创建矩阵
labelMat = mat(classLabels).T # 转置
m, n = shape(dataMatrix) # 获得矩阵的长宽
numSteps = 10.0
bestStump = {} # 创建一个字典,存储最佳结果
bestClasEst = mat(zeros((m, 1)))
minError = inf # 初始为无穷大
for i in range(n): # 遍历所有的列向量
rangeMin = dataMatrix[:, i].min()
rangeMax = dataMatrix[:, i].max()
stepSize = (rangeMax - rangeMin) / numSteps
for j in range(-1, int(numSteps) + 1): # 遍历当前方向
for inequal in ['lt', 'gt']: # 大于阈值和小于阈值
threshVal = (rangeMin + float(j) * stepSize) # 阈值
predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal) # 用单层决策树判断
errArr = mat(ones((m, 1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T * errArr # 将错误向量乘上样本权重D
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump, minError, bestClasEst
def adaBoostTrainDS(dataArr, classLabels, numIt=40): # 训练过程
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m, 1)) / m)
aggClassEst = mat(zeros((m, 1)))
for i in range(numIt):
bestStump, error, classEst = buildStump(dataArr, classLabels, D)
alpha = float(
0.5 * log((1.0 - error) / max(error, 1e-16)))
bestStump['alpha'] = alpha
weakClassArr.append(bestStump)
expon = multiply(-1 * alpha * mat(classLabels).T, classEst)
D = multiply(D, exp(expon))
D = D / D.sum()
aggClassEst += alpha * classEst
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m, 1)))
errorRate = aggErrors.sum() / m
print("total error: ", errorRate)
if errorRate == 0.0: break
return weakClassArr
def adaClassify(datToClass, classifierArr):
dataMatrix = mat(datToClass)
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m, 1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'], classifierArr[i]['thresh'],
classifierArr[i]['ineq'])
aggClassEst += classifierArr[i]['alpha'] * classEst
return sign(aggClassEst)
dataArr, labelArr = loadDataSet("D:/Desktop/horseColicTraining2.txt")
classifierArr = adaBoostTrainDS(dataArr, labelArr, 15)
testData, testY = loadDataSet("D:/Desktop/horseColicTest2.txt")
outputArr = adaClassify(testData, classifierArr)
print(outputArr.T)
errorArr = mat(ones((len(testData), 1)))
FinalerrorRate = errorArr[outputArr != mat(testY).T].sum() / float(errorArr.shape[0])
print("FinalerrorRate:", FinalerrorRate)
def draw(datMat, classLabels):
xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
for i in range(len(classLabels)):
if classLabels[i] == 1.0:
xcord1.append(datMat[i, 0]), ycord1.append(datMat[i, 1])
else:
xcord0.append(datMat[i, 0]), ycord0.append(datMat[i, 1])
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(xcord0, ycord0, marker='s', s=90)
ax.scatter(xcord1, ycord1, marker='o', s=50, c='red')
plt.title('decision stump test data')
plt.show()
3.房价预测
from matplotlib import pyplot as plt
from sklearn import neighbors
from sklearn import ensemble
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import csv
import numpy
fp = open('kc_house_data.csv')
fp_data = csv.reader(fp)
y = []
x = []
for line in fp_data:
if line[0] != 'id':
line[1] = line[1][0:8]
y.append(float(line[2]))
line.remove(line[2])
li = []
for i in line:
li.append(float(i))
x.append(li)
x = numpy.array(x)
y = numpy.array(y)
fp.close()
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 训练集与测试集之比
#adaboost算法(线性回归作为弱学习器)
adaboost = AdaBoostRegressor(LinearRegression())
adaboost.fit(x_train, y_train)
y_pre1 = adaboost.predict(x_test)
print("adaboost训练集分数:",adaboost.score(x_train,y_train))
print("adaboost验证集分数:",adaboost.score(x_test,y_test))
print('Adaboost算法(线性回归作为弱分类器)误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre1))
#线性回归作为学习器
Linear = LinearRegression()
Linear.fit(x_train, y_train)
y_pre2 = Linear.predict(x_test)
print("单个线性回归训练集分数:",Linear.score(x_train,y_train))
print("单个线性回归验证集分数:",Linear.score(x_test,y_test))
print('线性回归算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre2))
#adaboost算法(回归树作为弱学习器)
adaboost = AdaBoostRegressor(DecisionTreeRegressor())
adaboost.fit(x_train, y_train)
y_pre3 = adaboost.predict(x_test)
print('Adaboost算法(回归树)误差:')
print("adaboost回归树训练集分数:",adaboost.score(x_train,y_train))
print("adaboost回归树验证集分数:",adaboost.score(x_test,y_test))
print(mean_squared_error(y_true=y_test, y_pred=y_pre3))
#普通回归树作为学习器
decision_tree = DecisionTreeRegressor()
decision_tree.fit(x_train, y_train)
y_pre4 = decision_tree.predict(x_test)
print("普通回归树训练集分数:",decision_tree.score(x_train,y_train))
print("普通回归树验证集分数:",decision_tree.score(x_test,y_test))
print('普通回归树算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre4))
# 做ROC曲线
plt.figure()
plt.plot(range(len(y_pre1)), y_pre1, 'b', label="predict")
plt.plot(range(len(y_pre1)), y_test, 'r', label="test")
plt.legend(loc="upper right") # 显示图中的标签
plt.xlabel("the number of sales")
plt.ylabel('value of sales')
plt.show()
# KNN算法
adaboost = AdaBoostRegressor(neighbors.KNeighborsRegressor())
adaboost.fit(x_train, y_train)
y_pre5 = adaboost.predict(x_test)
print('Adaboost算法(KNN作为弱分类器)误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre5))
KN = neighbors.KNeighborsRegressor()
KN.fit(x_train, y_train)
y_pre5 = KN.predict(x_test)
print('KNN算法误差:')
print(mean_squared_error(y_true=y_test, y_pred=y_pre5))