05- 泰坦尼克号海难生死预测 (机器学习集成算法) (项目五)
- Kaggle: 一个数据建模和数据分析竞赛平台
- sns画柱状图: sns.barplot(data=train,x='Pclass',y='Survived')
- 查看数据分布(survived 和 fare): sns.FacetGrid(train,hue='Survived',aspect=3)
ageFacet=sns.FacetGrid(train,hue='Survived',aspect=3)
ageFacet.map(sns.kdeplot,'Fare',shade=True)
ageFacet.set(xlim=(0,150))
ageFacet.add_legend()- Cabin(船舱)缺失值填充:
full['Cabin']=full['Cabin'].fillna('U') # 利用U(Unknown)填充缺失值- 比较各种模型
# 不同机器学习交叉验证结果汇总
cv_results=[]
for classifier in classifiers:
cv_results.append(cross_val_score(classifier,experData_X,experData_y,
scoring='accuracy',cv=kfold,n_jobs=-1))
# 求出模型得分的均值和标准差
cv_means=[]
cv_std=[]
for cv_result in cv_results:
cv_means.append(cv_result.mean())
cv_std.append(cv_result.std())
# 汇总数据
cvResDf=pd.DataFrame({'cv_mean':cv_means,
'cv_std':cv_std,
'algorithm':['SVC','DecisionTreeCla','RandomForestCla',
'ExtraTreesCla',
'GradientBoostingCla','KNN','LR','LDA']})
cvResDf- 建立模型
GBC = GradientBoostingClassifier()
gb_param_grid = {'loss' : ["deviance"],
'n_estimators' : [100,200,300],
'learning_rate': [0.1, 0.05, 0.01],
'max_depth': [4, 8],
'min_samples_leaf': [100,150],
'max_features': [0.3, 0.1]
}
modelgsGBC = GridSearchCV(GBC,param_grid = gb_param_grid, cv=kfold,
scoring="accuracy", n_jobs= -1, verbose = 1)
modelgsGBC.fit(experData_X,experData_y)
在参与本次kaggle项目过程中,参考学习了很多其他竞赛方案的分析思路以及数据处理技巧,如:考虑同组效应、数据对数化处理、多种模型比较结果优劣等等。在项目过程中,主要从以下三个方面对模型改进来提升准确率:
- 模型选优:分别选取多种模型进行建模,根据模型评分进行初步比较,最终综合考虑多个性能指标来选择合适的预测模型;
- 特征挖掘与筛选:通过挖掘新的特征并测试选择不同特征时模型预测的准确性,来选择最终训练模型的特征集合;
- 数据整容:缺失值的填充方法以及“不合群”数据的处理也直接影响模型的最终预测结果。
- 项目地址: Titanic - Machine Learning from Disaster | Kaggle
1、背景介绍
泰坦尼克号于1909年3月31日在爱尔兰动工建造,1911年5月31日下水,次年4月2日完工试航。她是当时世界上体积最庞大、内部设施最豪华的客运轮船,有“永不沉没”的美誉。然而讽刺的是,泰坦尼克号首航便遭遇厄运:1912年4月10日她从英国南安普顿出发,途径法国瑟堡和爱尔兰昆士敦,驶向美国纽约。在14日晚23时40分左右,泰坦尼克号与一座冰山相撞,导致船体裂缝进水。次日凌晨2时20分左右,泰坦尼克号断为两截后沉入大西洋,其搭载的2224名船员及乘客,在本次海难中逾1500人丧生。
在学习机器学习相关项目时,Titanic生存率预测项目也通常是入门练习的经典案例。Kaggle平台为我们提供了一个竞赛案例“Titanic: Machine Learning from Disaster”,在该案例中,我们将探究什么样的人在此次海难中幸存的几率更高,并通过构建预测模型来预测乘客生存率。
本项目通过数据可视化理解数据,并利用特征工程等方法挖掘更多有价值的特征,然后利用同组效应找出共性较强的群体并对其数据进行修正,在选择模型时分别比较了Gradient Boosting Classifier、Logistic Regression等多种方法,最终利用Gradient Boosting Classifier对乘客的生存率进行预测。
2、加载数据
#导入相关包
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import seaborn as sns
#设置sns样式
sns.set(style='white',context='notebook',palette='muted')
import matplotlib.pyplot as plt
#导入数据
train=pd.read_csv('./train.csv')
test=pd.read_csv('./test.csv')
display(train.head())| PassengerId | Survived | Pclass | Name | Sex | Age |
|---|---|---|---|---|---|
| 乘客编号 | 是否生还 | 用户阶级 | 姓名 | 性别 | 年龄 |
| SibSp | Parch | Ticket | Fare | Cabin | Embarked |
| 兄弟姐妹配偶数 | 家长孩子数 | 船票号 | 乘客花费 | 船舱 | 港 |
Survived 是否存活(label):
- 0 - 用户死亡;
- 1- 用户存活;
Pclass(用户阶级):
- 1 - 1st class,高等用户;
- 2 - 2nd class,中等用户;
- 3 - 3rd class,低等用户;
SibSp:描述了泰坦尼克号上与乘客同行的兄弟姐妹(Siblings)和配偶(Spouse)数目;
Parch:描述了泰坦尼克号上与乘客同行的家长(Parents)和孩子(Children)数目;
Cabin(船舱):描述用户所住的船舱编号。由两部分组成,仓位号和房间编号,如C88中,C和88分别对应C仓位和88号房间;
Embarked(港口):
-
S:Southampton(南安普顿,英国);
-
C:Cherbourg(瑟堡,法国);
-
Q:Queenstown(昆士敦,英国);
3、数据探索
3.1、查看数据整体情况
#分别查看实验数据集和预测数据集数据
print('训练数据大小:',train.shape) # 训练数据大小: (891, 12)
print('预测数据大小:',test.shape) # 预测数据大小: (418, 11)
#将训练数据和预测数据合并,这样便于一起处理
full=train.append(test,ignore_index=True)
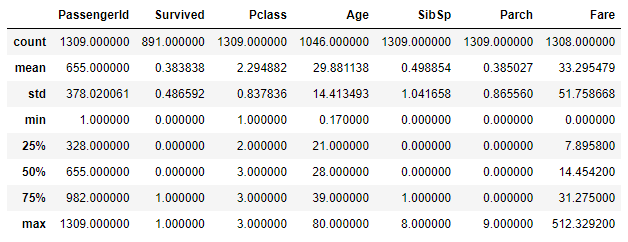
full.describe()- 无明显的异常值,几乎所有数据均在正常范围内。
full.info()- Age/Cabin/Embarked/Fare四项数据有缺失值,其中Cabin字段缺失近四分之三的数据。
3.2、特征与标签关系
3.2.1、Embarked与Survived关系
sns.barplot(data=train,x='Embarked',y='Survived')- 上船港口和生存率关系较大
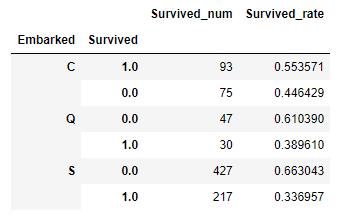
#计算不同类型Embarked的乘客,其生存率为多少
s = full.groupby('Embarked')['Survived'].value_counts().to_frame()
s2 = s/s.sum(level=0)
pd.merge(s,s2,left_index=True,right_index=True,suffixes=['_num','_rate'])- 不同的港口的幸存率, 法国登船乘客生存率较高原因可能与其头等舱乘客比例较高有关,因此继续查看不同登船地点乘客各舱位乘客数量情况。
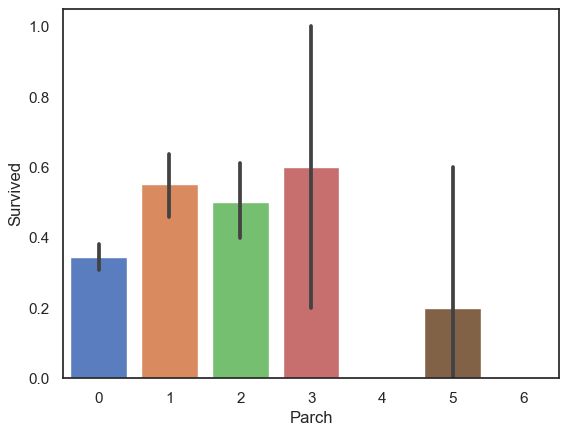
3.2.2、Parch与Survived关系
sns.barplot(data=train,x='Parch',y='Survived')- 当乘客同行的父母及子女数量适中时,生存率较高 , 孩子较多较少, 死亡率较高
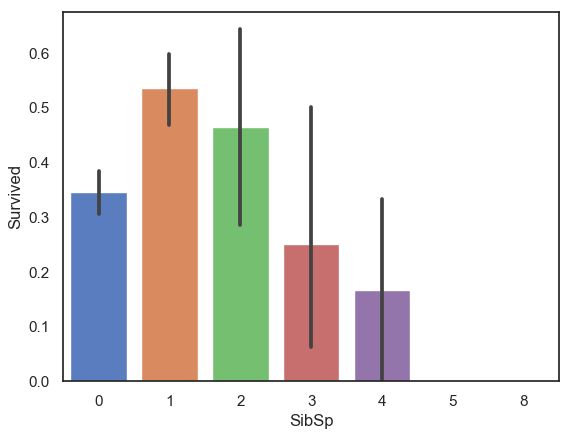
3.2.3、SibSp与Survived关系
sns.barplot(data=train,x='SibSp',y='Survived')- 当乘客同行的同辈数量适中时生存率较高
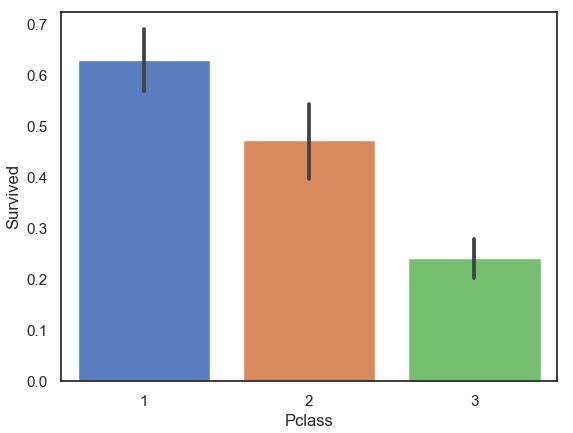
3.2.4、Pclass与Survived关系
sns.barplot(data=train,x='Pclass',y='Survived')- 乘客客舱等级越高,生存率越高
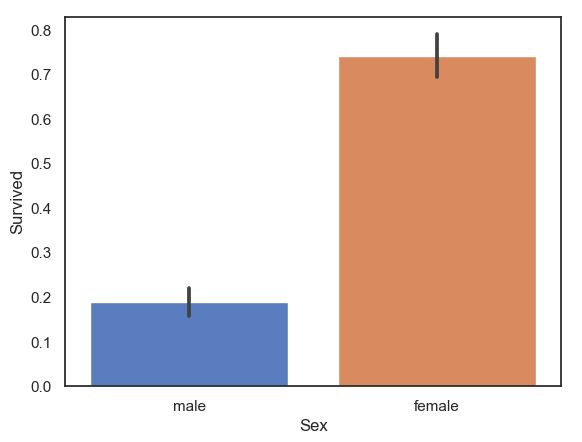
3.2.5、Sex与Survived关系
sns.barplot(data=train,x='Sex',y='Survived')- 女性的生存率远高于男性
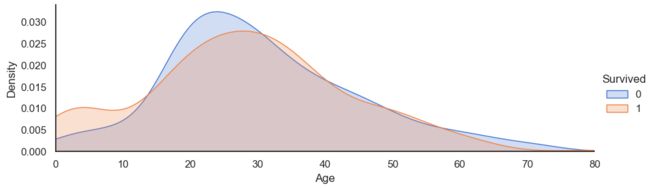
3.2.6、Age与Survived关系
#创建坐标轴
ageFacet=sns.FacetGrid(train,hue='Survived',aspect=3)
#作图,选择图形类型
ageFacet.map(sns.kdeplot,'Age',shade=True)
#其他信息:坐标轴范围、标签等
ageFacet.set(xlim=(0,train['Age'].max()))
ageFacet.add_legend()- 当乘客年龄段在0-10岁期间时生存率会较高
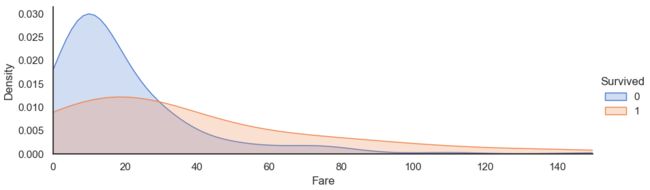
3.2.7、Fare与Survived关系
#创建坐标轴
ageFacet=sns.FacetGrid(train,hue='Survived',aspect=3)
ageFacet.map(sns.kdeplot,'Fare',shade=True)
ageFacet.set(xlim=(0,150))
ageFacet.add_legend()- 当票价低时乘客生存率较低,票价越高生存率一般越高!
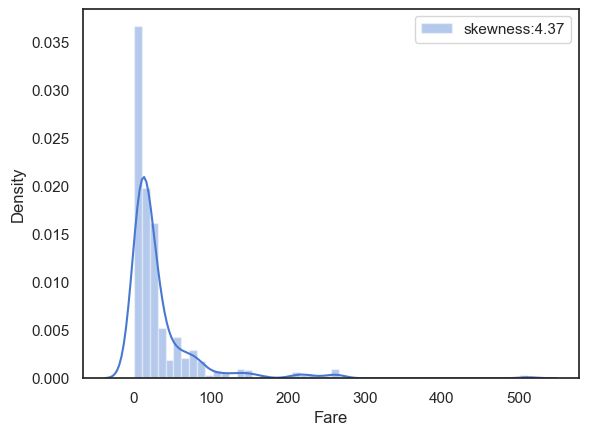
查看票价的分布
#查看fare分布
farePlot=sns.distplot(full['Fare'][full['Fare'].notnull()],
label='skewness:%.2f'%(full['Fare'].skew()))
farePlot.legend(loc='best')- fare的分布呈左偏的形态,其偏度skewness=4.37较大,说明数据偏移平均值较多,因此我们需要对数据进行对数化处理,防止数据权重分布不均匀。
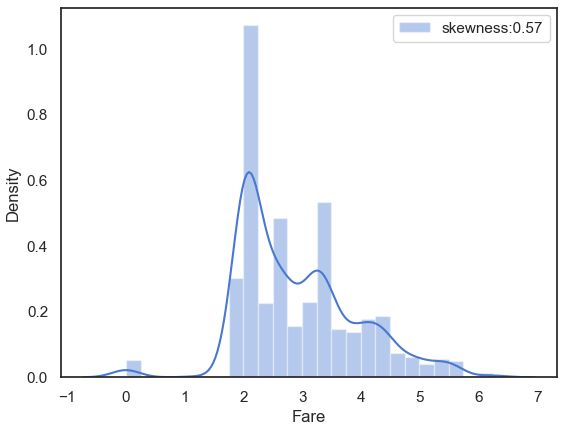
# 对数化处理fare值
full['Fare']=full['Fare'].map(lambda x: np.log(x) if x > 0 else x)
#处理之后票价Fare分布
farePlot=sns.distplot(full['Fare'][full['Fare'].notnull()],
label='skewness:%.2f'%(full['Fare'].skew()))
farePlot.legend(loc='best')
plt.savefig('./10-Fare票价分布.png',dpi = 200)- 对数化处理fare值
4、数据预处理
数据预处理主要包括以下四个方面内容:
- 数据清洗(缺失值以及异常值的处理)
- 特征工程(基于对现有数据特征的理解构造的新特征,以挖掘数据的更多特点)
- 同组识别(找出具有明显同组效应且违背整体规律的数据,对其进行规整)
- 筛选子集(对数据进行降维,选择子集)
4.1、数据清洗
- 对数据的缺失值、异常值进行处理,便于对数据进一步分析。本数据集有四个字段的数据存在缺失情况,即Cabin/Embarked/Fare/Age,未发现数据存在明显异常情况。
- 其中Age字段缺失较多且为连续型数值,将在进行4.2特征工程章节挖取更多特征后再填充缺失值。
4.1.1、Cabin(船舱)缺失值填充
# 对Cabin缺失值进行处理,利用U(Unknown)填充缺失值
full['Cabin']=full['Cabin'].fillna('U')
full['Cabin'].head()4.1.2、Embarked(港口)缺失值填充
# 对Embarked缺失值进行处理,查看缺失值情况
display(full[full['Embarked'].isnull()])
display(full['Embarked'].value_counts())
# 查看Embarked数据分布情况,可知在英国南安普顿登船可能性最大,因此以此填充缺失值。
full['Embarked']=full['Embarked'].fillna('S')4.1.3、Fare缺失值填充(乘客费用)
#查看缺失数据情况,该乘客乘坐3等舱,登船港口为法国,舱位未知
display(full[full['Fare'].isnull()])
# 利用3等舱,登船港口为英国,舱位未知旅客的平均票价来填充缺失值。
price = full[(full['Pclass']==3)&(full['Embarked']=='S')&(
full['Cabin']=='U')]['Fare'].mean()
full['Fare']=full['Fare'].fillna(price)
full.info()4.2、特征工程
在理解原数据特征的基础上,特征工程通过对原有数据进行整合处理,得到新特征以反映数据更多信息。
4.2.1、Name中的头衔信息-Title
旅客姓名数据中包含头衔信息,不同头衔也可以反映旅客的身份,而不同身份的旅客其生存率有可能会出现较大差异。因此我们通过Name特征提取旅客头衔Title信息,并分析Title与Survived之间的关系。
# 构造新特征Title
full['Title']=full['Name'].map(lambda x:x.split(',')[1].split('.')[0].strip())
# 查看title数据分布
full['Title'].value_counts()将相近的Title信息整合在一起:
#将title信息进行整合
TitleDict={}
TitleDict['Mr']='Mr'
TitleDict['Mlle']='Miss'
TitleDict['Miss']='Miss'
TitleDict['Master']='Master'
TitleDict['Jonkheer']='Master'
TitleDict['Mme']='Mrs'
TitleDict['Ms']='Mrs'
TitleDict['Mrs']='Mrs'
TitleDict['Don']='Royalty'
TitleDict['Sir']='Royalty'
TitleDict['the Countess']='Royalty'
TitleDict['Dona']='Royalty'
TitleDict['Lady']='Royalty'
TitleDict['Capt']='Officer'
TitleDict['Col']='Officer'
TitleDict['Major']='Officer'
TitleDict['Dr']='Officer'
TitleDict['Rev']='Officer'
full['Title']=full['Title'].map(TitleDict)
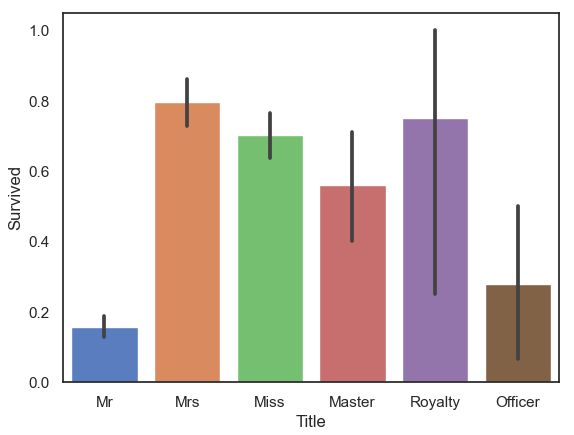
full['Title'].value_counts()可视化观察新特征与标签间关系:
#可视化分析Title与Survived之间关系
sns.barplot(data=full,x='Title',y='Survived')- 头衔为'Mr'及'Officer'的乘客,生存率明显较低。
4.2.2、FamilyNum及FamilySize信息
将Parch及SibSp字段整合得到一名乘客同行家庭成员总人数FamilyNum的字段,再根据家庭成员具体人数的多少得到家庭规模FamilySize这个新字段。
-
SibSp:描述了泰坦尼克号上与乘客同行的兄弟姐妹(Siblings)和配偶(Spouse)数目;
-
Parch:描述了泰坦尼克号上与乘客同行的家长(Parents)和孩子(Children)数目;
full['familyNum']=full['Parch']+full['SibSp'] + 1
#查看familyNum与Survived
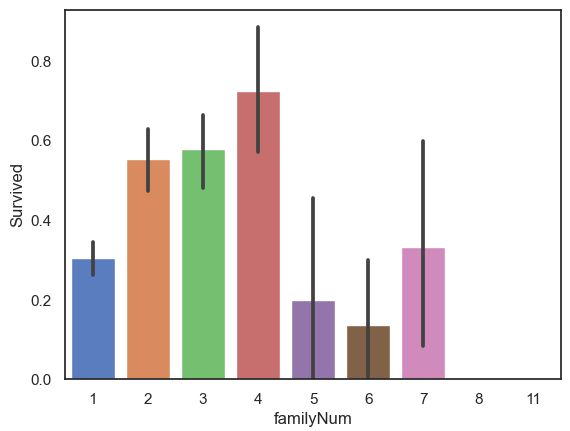
sns.barplot(data=full,x='familyNum',y='Survived')- 家庭成员人数在2-4人时,乘客的生存率较高,当没有家庭成员同行或家庭成员人数过多时生存率较低。
# 我们按照家庭成员人数多少,将家庭规模分为小(0)、中(1)、大(2)三类:
def familysize(familyNum):
if familyNum== 0 :
return 0
elif (familyNum>=1)&(familyNum<=3):
return 1
else:
return 2
full['familySize']=full['familyNum'].map(familysize)
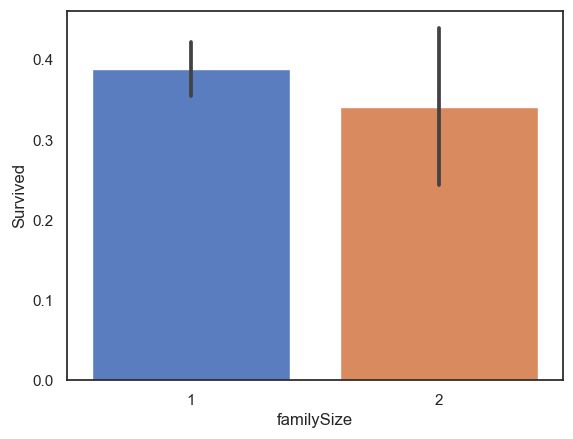
full['familySize'].value_counts()查看 familySize 与 Survived 关系:
# 查看familySize与Survived
sns.barplot(data=full,x='familySize',y='Survived')- 当家庭规模适中时,乘客的生存率更高。
4.2.3、Cabin客舱类型信息-Deck
Cabin字段的首字母代表客舱的类型,也反映不同乘客群体的特点,可能也与乘客的生存率相关。泰坦尼克号撞击冰山时,也跟客舱位置有一定关系
# 提取Cabin字段首字母
full['Deck']=full['Cabin'].map(lambda x:x[0])
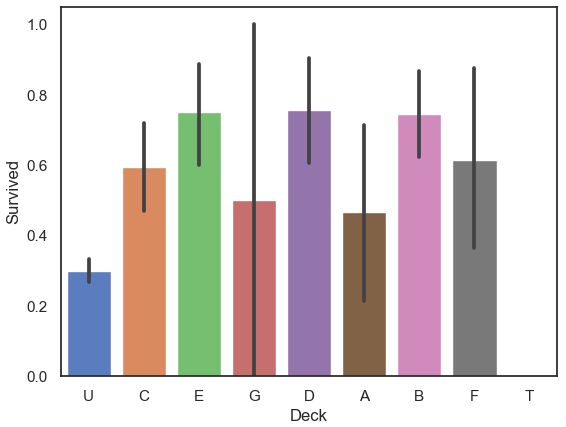
# 查看不同Deck类型乘客的生存率
sns.barplot(data=full,x='Deck',y='Survived')
plt.savefig('./14-Deck与Survived关系.png',dpi = 200)- 当乘客的客舱类型为B/D/E时,生存率较高;当客舱类型为U/T时,生存率较低。
4.2.4、共票号乘客数量TickCom及TickGroup
同一票号的乘客数量可能不同,可能也与乘客生存率有关系
#提取各票号的乘客数量
TickCountDict=full['Ticket'].value_counts()
TickCountDict.head()
'''
CA. 2343 11
1601 8
CA 2144 8
347077 7
PC 17608 7
Name: Ticket, dtype: int64
'''#将同票号乘客数量数据并入数据集中
full['TickCom']=full['Ticket'].map(TickCountDict)
full['TickCom'].head()
#查看TickCom与Survived之间关系
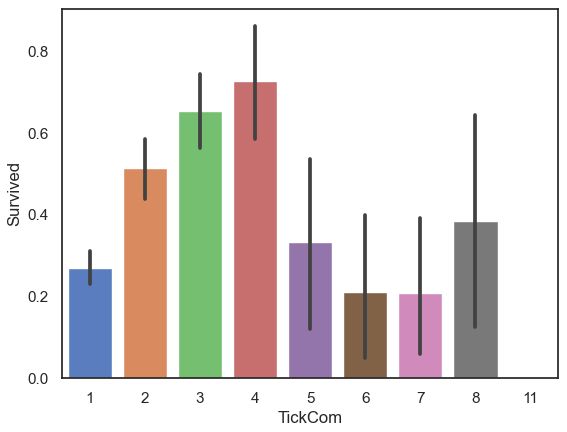
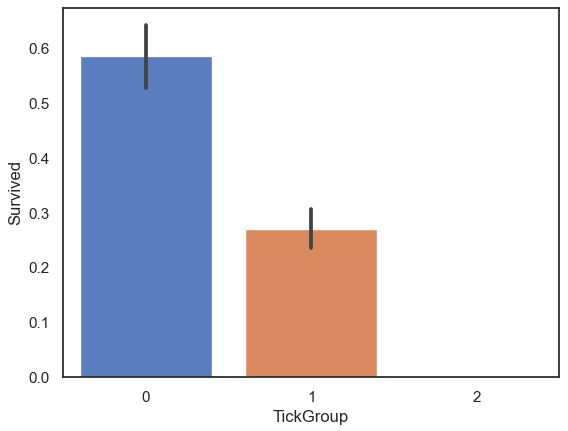
sns.barplot(data=full,x='TickCom',y='Survived')- 当TickCom大小适中时,乘客生存率较高。
# 按照TickCom大小,将TickGroup分为三类。
def TickCountGroup(num):
if (num>=2)&(num<=4):
return 0
elif (num==1)|((num>=5)&(num<=8)):
return 1
else :
return 2
# 得到各位乘客TickGroup的类别
full['TickGroup']=full['TickCom'].map(TickCountGroup)
# 查看TickGroup与Survived之间关系
sns.barplot(data=full,x='TickGroup',y='Survived')4.2.5、Age缺失值填充-构建随机森林模型预测缺失的数据
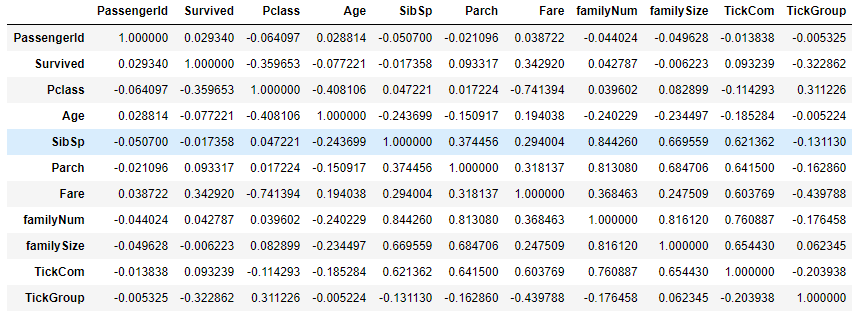
- 查看Age与Parch、Pclass、Sex、SibSp、Title、familyNum、familySize、Deck、TickCom、TickGroup等变量的相关系数大小,筛选出相关性较高的变量构建预测模型。
full[full['Age'].notnull()].corr()
# 筛选:Pclass、SibSp、Parch、Fare、familyNum、familySize、TickCom1、筛选数据
#筛选数据集
agePre=full[['Age','Parch','Pclass','SibSp','familyNum','TickCom','Title']]
# 进行one-hot编码
agePre=pd.get_dummies(agePre)
ageCorrDf=agePre.corr()
ageCorrDf['Age'].sort_values()2、拆分数据并建立模型(利用随机森林构建模型)
#拆分实验集和预测集
ageKnown=agePre[agePre['Age'].notnull()]
ageUnKnown=agePre[agePre['Age'].isnull()]
#生成实验数据的特征和标签
ageKnown_X=ageKnown.drop(['Age'],axis=1)
ageKnown_y=ageKnown['Age']
#生成预测数据的特征
ageUnKnown_X=ageUnKnown.drop(['Age'],axis=1)
#利用随机森林构建模型
from sklearn.ensemble import RandomForestRegressor
rfr=RandomForestRegressor(random_state=None,n_estimators=500,n_jobs=-1)
rfr.fit(ageKnown_X,ageKnown_y)3、利用模型进行预测并填入原数据集中
#模型得分
score = rfr.score(ageKnown_X,ageKnown_y)
print('模型预测年龄得分是:',score)
#预测年龄
ageUnKnown_predict = rfr.predict(ageUnKnown_X)
#填充预测数据
full.loc[full['Age'].isnull(),['Age']]=ageUnKnown_predict
full.info() #此时已无缺失值4.3、同组识别
虽然通过分析数据已有特征与标签的关系可以构建有效的预测模型,但是部分具有明显共同特征的用户可能与整体模型逻辑并不一致。如果将这部分具有同组效应的用户识别出来并对其数据加以修正,就可以有效提高模型的准确率。在Titanic案例中,我们主要探究相同姓氏的乘客是否存在明显的同组效应。
提取两部分数据,分别查看其“姓氏”是否存在同组效应(因为性别和年龄与乘客生存率关系最为密切,因此用这两个特征作为分类条件):
4.3.1 同姓氏的男性
12岁以上男性:找出男性中同姓氏均获救的部分; 女性以及年龄在12岁以下儿童:找出女性及儿童中同姓氏均遇难的部分。
#提取乘客的姓氏及相应的乘客数
full['Surname']=full['Name'].map(lambda x:x.split(',')[0].strip())
SurNameDict=full['Surname'].value_counts()
full['SurnameNum']=full['Surname'].map(SurNameDict)
# 12岁以上男性:找出男性中同姓氏均获救的部分
MaleDf=full[(full['Sex']=='male')&(full['Age']>12)&(full['familyNum']>=2)]
#分析男性同组效应
MSurNamDf=MaleDf['Survived'].groupby(MaleDf['Surname']).mean()
MSurNamDf.head()
MSurNamDf.value_counts()
'''
0.0 89
1.0 19
0.5 3'''- 大多数同姓氏的男性存在“同生共死”的特点,因此利用该同组效应,我们对生存率为1的姓氏里的男性数据进行修正,提升其预测为“可以幸存”的概率。
4.3.2 女性及儿童同组效应分析
#提取乘客的姓氏及相应的乘客数
full['Surname']=full['Name'].map(lambda x:x.split(',')[0].strip())
SurNameDict=full['Surname'].value_counts()
full['SurnameNum']=full['Surname'].map(SurNameDict)
#将数据分为两组
FemChildDf=full[((full['Sex']=='female')|(full['Age']<=12))&(full['familyNum']>=2)]
FCSurNamDf=FemChildDf['Survived'].groupby(FemChildDf['Surname']).mean()
FCSurNamDf.head()
FCSurNamDf.value_counts()
'''
1.000000 115
0.000000 27
0.750000 2
0.333333 1
0.142857 1'''与男性组特征相似,女性及儿童也存在明显的“同生共死”的特点,因此利用同组效应,对生存率为0的姓氏里的女性及儿童数据进行修正,提升其预测为“并未幸存”的概率。
4.3.3 数据集中修改
对数据集中这些姓氏的两组数据数据分别进行修正:
男性数据修正为:1、性别改为女;2、年龄改为5;
女性及儿童数据修正为:1、性别改为男;2、年龄改为60。
#获得生存率为1的姓氏
MSurNamDict=MSurNamDf[MSurNamDf.values==1].index
MSurNamDict
#获得生存率为0的姓氏
FCSurNamDict=FCSurNamDf[FCSurNamDf.values==0].index
FCSurNamDict
#对数据集中这些姓氏的男性数据进行修正:1、性别改为女;2、年龄改为5。
full.loc[(full['Survived'].isnull())&(full['Surname'].isin(
MSurNamDict))&(full['Sex']=='male'),'Sex']='female'
full.loc[(full['Survived'].isnull())&(full['Surname'].isin(
MSurNamDict))&(full['Sex']=='male'),'Age']=5
#对数据集中这些姓氏的女性及儿童的数据进行修正:1、性别改为男;2、年龄改为60。
full.loc[(full['Survived'].isnull())&(full['Surname'].isin(FCSurNamDict))&((
full['Sex']=='female')|(full['Age']<=12)),'Sex']='male'
full.loc[(full['Survived'].isnull())&(full['Surname'].isin(FCSurNamDict))&((
full['Sex']=='female')|(full['Age']<=12)),'Age']=604.4、筛选子集
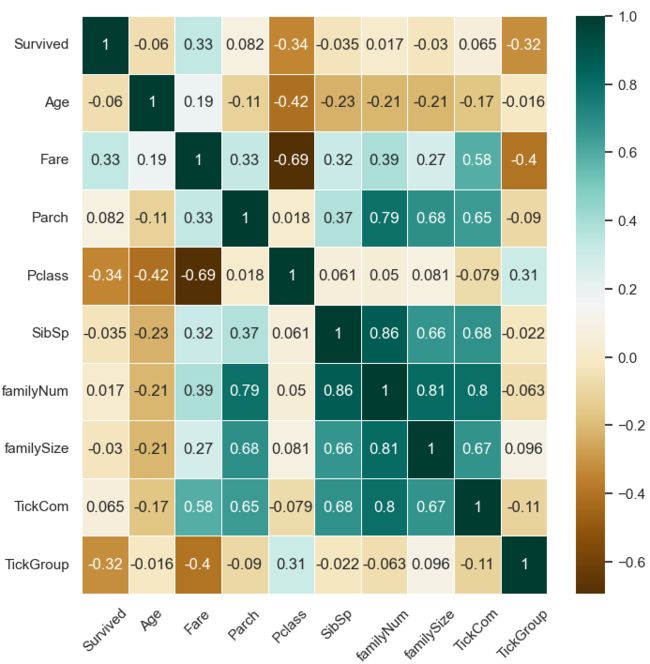
在对数据进行分析处理的过程中,数据的维度更高了,为提升数据有效性需要对数据进行降维处理。通过找出与乘客生存率“Survived”相关性更高的特征,剔除重复的且相关性较低的特征,从而实现数据降维。
#人工筛选
fullSel=full.drop(['Cabin','Name','Ticket','PassengerId','Surname',
'SurnameNum'],axis=1)
#查看各特征与标签的相关性
corrDf=pd.DataFrame()
corrDf=fullSel.corr()
corrDf['Survived'].sort_values(ascending=True)- 通过热力图,查看Survived与其他特征间相关性大小。
#热力图,查看Survived与其他特征间相关性大小
plt.figure(figsize=(8,8))
sns.heatmap(fullSel[['Survived','Age','Embarked','Fare','Parch','Pclass',
'Sex','SibSp','Title','familyNum','familySize','Deck',
'TickCom','TickGroup']].corr(),cmap='BrBG',annot=True,
linewidths=.5)
_ = plt.xticks(rotation=45)# 删除相关性系数低的属性
fullSel=fullSel.drop(['Age','Parch','SibSp','familyNum','TickCom'],axis=1)
#one-hot编码
fullSel=pd.get_dummies(fullSel)
fullSel.head()5、构建模型
本项目比较了SCV/Decision Tree/Gradient Boosting/LDA/KNN/Logistic Regression等多种机器学习算法的结果,并对表现较好的算法做进一步的对比,最终选择Gradient Boosting对乘客生存率进行预测。
5.1、模型选择
5.1.1、建立模型
主要考虑使用以下常用的机器学习算法进行比较:
- SCV
- Decision Tree
- Extra Trees
- Gradient Boosting
- Random Forest
- KNN
- Logistic Regression
- Linear Discriminant Analysis
#拆分实验数据与预测数据
experData=fullSel[fullSel['Survived'].notnull()]
preData=fullSel[fullSel['Survived'].isnull()]
experData_X=experData.drop('Survived',axis=1)
experData_y=experData['Survived']
preData_X=preData.drop('Survived',axis=1)
#导入机器学习算法库
from sklearn.ensemble import RandomForestClassifier,GradientBoostingClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV,cross_val_score,StratifiedKFold
#设置kfold,交叉采样法拆分数据集
kfold=StratifiedKFold(n_splits=10)
#汇总不同模型算法
classifiers=[]
classifiers.append(SVC())
classifiers.append(DecisionTreeClassifier())
classifiers.append(RandomForestClassifier())
classifiers.append(ExtraTreesClassifier())
classifiers.append(GradientBoostingClassifier())
classifiers.append(KNeighborsClassifier())
classifiers.append(LogisticRegression())
classifiers.append(LinearDiscriminantAnalysis())5.1.2、比较各种算法结果,进一步选择模型
#不同机器学习交叉验证结果汇总
cv_results=[]
for classifier in classifiers:
cv_results.append(cross_val_score(classifier,experData_X,experData_y,
scoring='accuracy',cv=kfold,n_jobs=-1))
#求出模型得分的均值和标准差
cv_means=[]
cv_std=[]
for cv_result in cv_results:
cv_means.append(cv_result.mean())
cv_std.append(cv_result.std())
#汇总数据
cvResDf=pd.DataFrame({'cv_mean':cv_means,
'cv_std':cv_std,
'algorithm':['SVC','DecisionTreeCla','RandomForestCla',
'ExtraTreesCla',
'GradientBoostingCla','KNN','LR','LDA']})
cvResDf
'''
cv_mean cv_std algorithm
0 0.835019 0.035179 SVC
1 0.810337 0.028974 DecisionTreeCla
2 0.821548 0.034612 RandomForestCla
3 0.815955 0.028821 ExtraTreesCla
4 0.828302 0.038513 GradientBoostingCla
5 0.823808 0.040767 KNN
6 0.830549 0.038304 LR
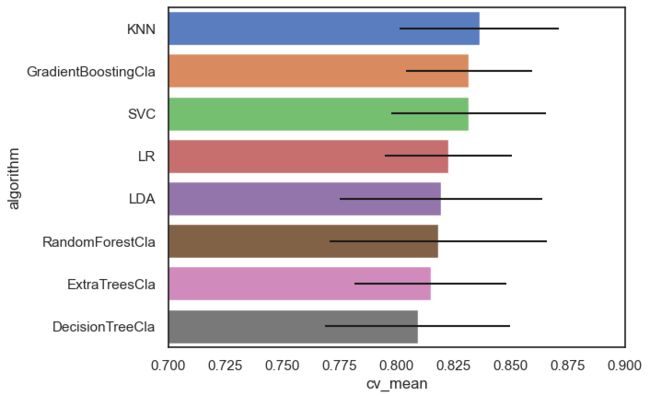
7 0.828327 0.039658 LDA'''可视化查看不同算法的表现情况
bar = sns.barplot(data=cvResDf.sort_values(by='cv_mean',ascending=False),
x='cv_mean',y='algorithm',**{'xerr':cv_std})
bar.set(xlim = (0.7,0.9))KNN、SVC、LR、LDA以及GradientBoostingCla 模型在该问题中表现较好。
5.1.3、模型调优
综合以上模型表现,考虑选择SVC、LDA、GradientBoostingCla、LR四种模型进一步对比。分别建立对应模型,并进行模型调优。
#GradientBoostingClassifier模型
GBC = GradientBoostingClassifier()
gb_param_grid = {'loss' : ["deviance"],
'n_estimators' : [100,200,300],
'learning_rate': [0.1, 0.05, 0.01],
'max_depth': [4, 8],
'min_samples_leaf': [100,150],
'max_features': [0.3, 0.1]
}
modelgsGBC = GridSearchCV(GBC,param_grid = gb_param_grid, cv=kfold,
scoring="accuracy", n_jobs= -1, verbose = 1)
modelgsGBC.fit(experData_X,experData_y)
#LogisticRegression模型
modelLR=LogisticRegression()
LR_param_grid = {'C' : [1,2,3],
'penalty':['l1','l2']}
modelgsLR = GridSearchCV(modelLR,param_grid = LR_param_grid, cv=kfold,
scoring="accuracy", n_jobs= -1, verbose = 1)
modelgsLR.fit(experData_X,experData_y)
#SVC模型
svc = SVC()
gb_param_grid = {'C' : [0.1,0.5,1,2,3,5,10],
'kernel':['rbf','poly','sigmoid']
}
modelgsSVC = GridSearchCV(svc,param_grid = gb_param_grid, cv=kfold,
scoring="accuracy", n_jobs= -1, verbose = 1)
modelgsSVC.fit(experData_X,experData_y)
#LDA模型
lda = LinearDiscriminantAnalysis()
gb_param_grid = {'solver' : ['svd', 'lsqr', 'eigen'],
'tol':[0.000001,0.00001,0.0001,0.001,0.01]
}
modelgsLDA = GridSearchCV(lda,param_grid = gb_param_grid, cv=kfold,
scoring="accuracy", n_jobs= -1, verbose = 1)
modelgsLDA.fit(experData_X,experData_y)5.2、模型评估
5.2.1、查看模型准确率
#modelgsGBC模型
print('modelgsGBC模型得分为:%.3f'%modelgsGBC.best_score_)
#modelgsLR模型
print('modelgsLR模型得分为:%.3f'%modelgsLR.best_score_)
#modelgsSVC模型
print('modelgsSVC模型得分为:%.3f'%modelgsSVC.best_score_)
#modelgsLDA模型
print('modelgsLDA模型得分为:%.3f'%modelgsLDA.best_score_)
'''
modelgsGBC模型得分为:0.840
modelgsLR模型得分为:0.823
modelgsSVC模型得分为:0.832
modelgsLDA模型得分为:0.819'''GBC模型得分(即模型准确性)更高,继续比较其他指标的差异。
5.2.2、查看模型ROC曲线
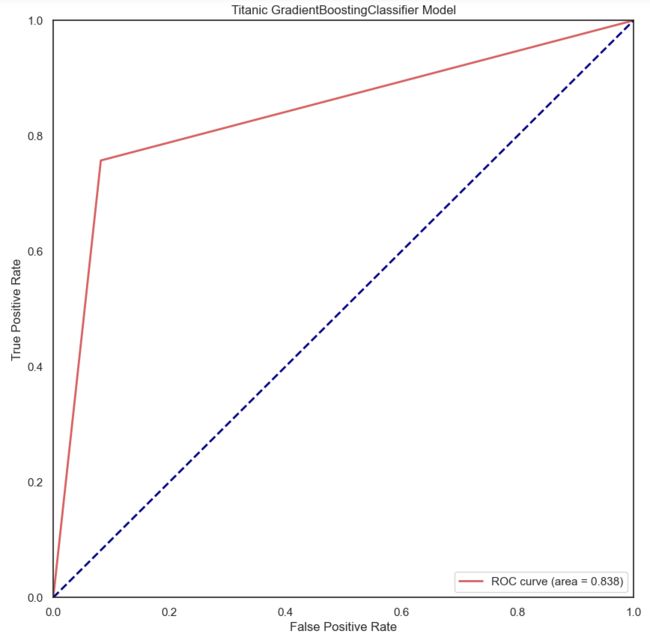
#查看模型ROC曲线
#求出测试数据模型的预测值
modelgsGBCtestpre_y=modelgsGBC.predict(experData_X).astype(int)
#画图
from sklearn.metrics import roc_curve, auc ###计算roc和auc
# Compute ROC curve and ROC area for each class
#计算真正率和假正率
fpr,tpr,threshold = roc_curve(experData_y, modelgsGBCtestpre_y)
roc_auc = auc(fpr,tpr) ###计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
# 假正率为横坐标,真正率为纵坐标做曲线
plt.plot(fpr, tpr, color='r',
lw=lw, label='ROC curve (area = %0.3f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Titanic GradientBoostingClassifier Model')
plt.legend(loc="lower right")
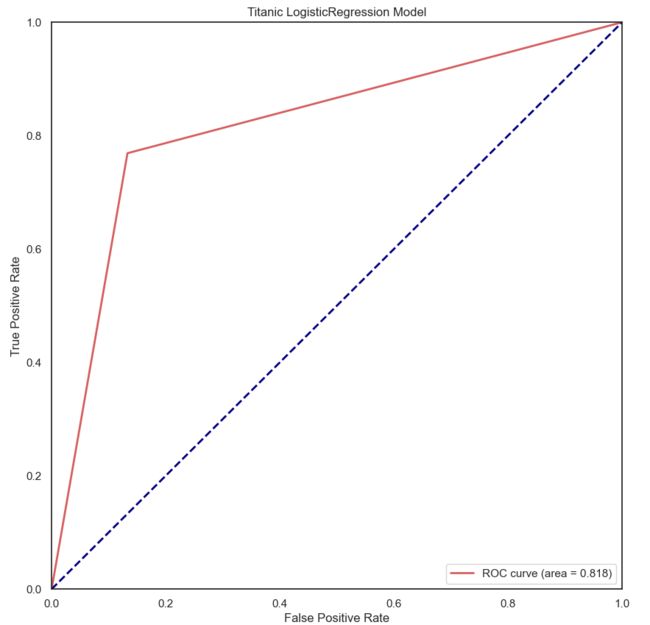
plt.show()#查看模型ROC曲线
#求出测试数据模型的预测值
modelgsLRtestpre_y=modelgsLR.predict(experData_X).astype(int)
#画图
from sklearn.metrics import roc_curve, auc ###计算roc和auc
# Compute ROC curve and ROC area for each class
# 计算真正率和假正率
fpr,tpr,threshold = roc_curve(experData_y, modelgsLRtestpre_y)
roc_auc = auc(fpr,tpr) ###计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
# 假正率为横坐标,真正率为纵坐标做曲线
plt.plot(fpr, tpr, color='r',
lw=lw, label='ROC curve (area = %0.3f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Titanic LogisticRegression Model')
plt.legend(loc="lower right")
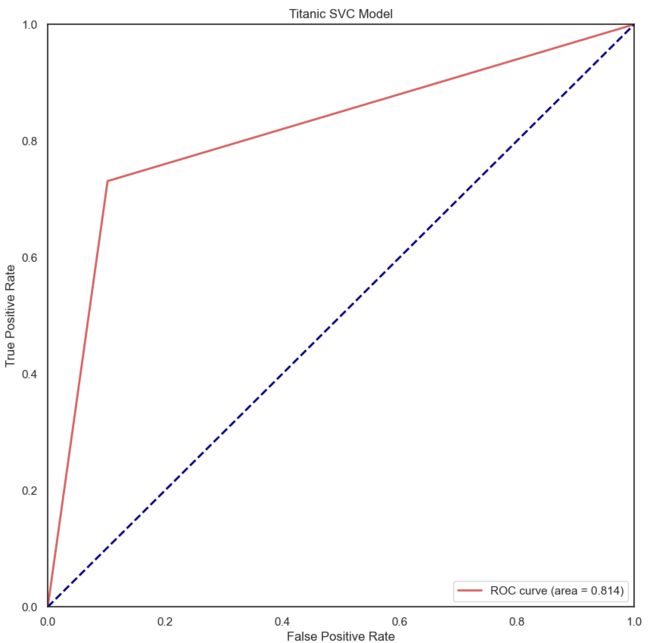
plt.show()#查看模型ROC曲线
#求出测试数据模型的预测值
modelgsSVCtestpre_y=modelgsSVC.predict(experData_X).astype(int)
#画图
from sklearn.metrics import roc_curve, auc ###计算roc和auc
# Compute ROC curve and ROC area for each class
# 计算真正率和假正率
fpr,tpr,threshold = roc_curve(experData_y, modelgsSVCtestpre_y)
roc_auc = auc(fpr,tpr) ###计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
# 假正率为横坐标,真正率为纵坐标做曲线
plt.plot(fpr, tpr, color='r',
lw=lw, label='ROC curve (area = %0.3f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Titanic SVC Model')
plt.legend(loc="lower right")
plt.show()- GBDT、LR和SVC模型ROC曲线均左上偏,AUC分别为0.838和0.825、0.818,即GradientBoostingClassifier模型效果较好。
5.2.3、查看混淆矩阵
#混淆矩阵
from sklearn.metrics import confusion_matrix
print('GradientBoostingClassifier模型混淆矩阵为\n',confusion_matrix(experData_y,
modelgsGBCtestpre_y))
print('LogisticRegression模型混淆矩阵为\n',confusion_matrix(experData_y,
modelgsLRtestpre_y))
print('SVC模型混淆矩阵为\n',confusion_matrix(experData_y,
modelgsSVCtestpre_y))
''' GradientBoostingClassifier模型混淆矩阵为
[[501 48]
[ 81 261]]
LogisticRegression模型混淆矩阵为
[[480 69]
[ 77 265]]
SVC模型混淆矩阵为
[[492 57]
[ 89 253]] '''0表示死亡,1表示存活
通过混淆矩阵可以看出:
- GBDT模型真正率TPR为503/(503 + 46) = 912,假正率FPR为0.236,
- LR模型真正率TPR为0.874,假正率FPR为0.225,
- SVC模型真正率TPR为0.896,假正率FPR为0.260
说明GBS找出正例能力很强,同时也不易将负例错判为正例。 综合考虑,本项目中将利用GBC方法进行模型预测。
综上所述,选择GBDT模型比较好~
6、模型预测
利用模型进行预测,并按规则导出预测结果
#TitanicGBSmodle
GBCpreData_y=modelgsGBC.predict(preData_X)
GBCpreData_y=GBCpreData_y.astype(int)
#导出预测结果
GBCpreResultDf=pd.DataFrame()
GBCpreResultDf['PassengerId']=full['PassengerId'][full['Survived'].isnull()]
GBCpreResultDf['Survived']=GBCpreData_y
GBCpreResultDf
#将预测结果导出为csv文件
GBCpreResultDf.to_csv('./TitanicGBCmodle_lufengkun.csv',index=False)将结果上传至Kaggle中,最终预测得分为0.79186,排名约TOP3%。
在参与本次kaggle项目过程中,参考学习了很多其他竞赛方案的分析思路以及数据处理技巧,如:考虑同组效应、数据对数化处理、多种模型比较结果优劣等等。在项目过程中,主要从以下三个方面对模型改进来提升准确率:
- 模型选优:分别选取多种模型进行建模,根据模型评分进行初步比较,最终综合考虑多个性能指标来选择合适的预测模型;
- 特征挖掘与筛选:通过挖掘新的特征并测试选择不同特征时模型预测的准确性,来选择最终训练模型的特征集合;
- 数据整容:缺失值的填充方法以及“不合群”数据的处理也直接影响模型的最终预测结果。