06- 信用卡反欺诈 (机器学习集成算法) (项目六)

本项目为 kaggle 项目

• 项目难点在于: 盗刷的比例占总数据量的比例较低, 直接预测为非盗刷也有 99.8%+ 的准确率.

• data.info()      # 查看所有信息
• msno.matrix(data)    # 查看缺失值
• axis=1 时       # 删除列
• 显示颜色种类

from matplotlib import colors
plt.colormaps()  # 'magma','inferno','plasma','cividis', 'twilight'

• 查看数据模型的对比

plt.rcParams['font.family'] = 'STKaiti'
v_feat = data.iloc[:,1:29].columns
plt.figure(figsize=(16,4 * 28))
cond1 = data['Class'] == 1
cond2 = data['Class'] == 0

gs = gridspec.GridSpec(28,1) # 子视图
for i,cn in enumerate(v_feat):
    ax = plt.subplot(gs[i])
    sns.distplot(data[cn][cond1],bins = 50) # 欺诈
    sns.distplot(data[cn][cond2],bins = 100) # 正常消费
    ax.set_title('特征概率分布图' + cn)

• 归一化处理

col = ['Amount','Hour']
sc = StandardScaler()   # Z-score归一化
data_new[col] = sc.fit_transform(data_new[col])

• 样本不平衡常用的解决方法有过采样和欠采样, 本项目处理不平衡采用的是过采样的方法 .

# pip install imblearn
from imblearn.over_sampling import SMOTE # 近邻规则，创造一些新数据
smote = SMOTE()
# X，y是数据
X,y = smote.fit_resample(X,y)

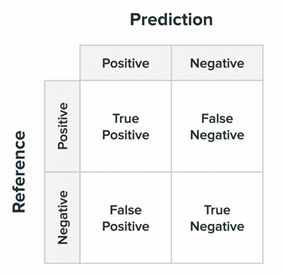
• 召回率(Recall):  表示的是样本中的正例有多少被预测正确了（找得全）所有正例中被正确预测出来的比例。
• 混淆矩阵 (Confusion Matrix):plot confusion matrix是一种将混滑矩阵可视化的方法。混阵是一种用于评估分类器性能的工具，它显示了预测值和真实值之间的关系。使用 pilot confusion matrix 可以将混淆矩阵以图形的形式呈现出来，方便观察和理解分类器的性能。

• ROC曲线：ROC（Receiver Operating Characteristic）曲线是以假正率（FP_rate）和真正率（TP_rate）为轴的曲线，ROC曲线下面的面积我们叫做AUC.曲线与FP_rate轴 围成的面积（记作AUC）越大，说明性能越好
• 训练模型

param_grid = {'C': [0.01,0.1, 1, 10, 100, 1000,],'penalty': [ 'l1', 'l2']}
# 确定模型LogisticRegression，和参数组合param_grid ，cv指定10折
grid_search = GridSearchCV(LogisticRegression(),param_grid,cv=10) 
grid_search.fit(X_train, y_train)    # 使用训练集学习算法

---

1、项目介绍

1.1、本项目需解决的问题

本项目通过利用信用卡的历史交易数据，进行机器学习，构建信用卡反欺诈预测模型，提前发现客户信用卡被盗刷的事件。

1.2、建模思路

1.3、项目背景

数据集包含由欧洲持卡人于2013年9月使用信用卡进行交的数据。此数据集显示两天内发生的交易，其中284,807笔交易中有492笔被盗刷。数据集非常不平衡，积极的类（被盗刷）占所有交易的0.172％。
它只包含作为PCA转换结果的数字输入变量。不幸的是，由于保密问题，我们无法提供有关数据的原始功能和更多背景信息。特征V1，V2，... V28是使用PCA获得的主要组件，没有用PCA转换的唯一特征是“时间”和“量”。特征'时间'包含数据集中每个事务和第一个事务之间经过的秒数。特征“金额”是交易金额，此特征可用于实例依赖的成本认知学习。特征'类'是响应变量，如果发生被盗刷，则取值1，否则为0。

2、场景解析

2.1、算法选择

首先，我们拿到的数据是持卡人两天内的信用卡交易数据，这份数据包含很多维度，要解决的问题是预测持卡人是否会发生信用卡被盗刷。信用卡持卡人是否会发生被盗刷只有两种可能，发生被盗刷或不发生被盗刷。又因为这份数据是打标好的，也就是说它是一个监督学习的场景。于是，我们判定信用卡持卡人是否会发生被盗刷是一个二元分类问题，意味着可以通过二分类相关的算法来找到具体的解决办法，本项目选用的算法是逻辑斯蒂回归（Logistic Regression）。

2.2、数据分析

数据是结构化数据 ，不需要做特征抽象（是针对有序和无序的文本分类型特征，采用不同的方法进行处理，将其类别属性数值化）。特征V1至V28是经过PCA处理，而特征Time和Amount的数据规格与其他特征差别较大，需要对其做特征缩放，将特征缩放至同一个规格。在数据质量方面 ，没有出现乱码或空字符的数据，可以确定字段Class为目标列，其他列为特征列。

2.3、模型评估

这份数据是全部打标好的数据，可以通过交叉验证的方法对训练集生成的模型进行评估。80%的数据进行训练，20%的数据进行预测和评估。

2.4、场景总结

现对该业务场景进行总结如下：

• 根据历史记录数据学习并对信用卡持卡人是否会发生被盗刷进行预测，二分类监督学习场景，选择逻辑斯蒂回归（Logistic Regression）算法。
• 数据为结构化数据，不需要做特征抽象，但需要做特征缩放。

3、数据预处理

3.1、导包

import numpy as np
import pandas as pd
pd.set_option('display.float_format',lambda x :'%.4f' % x)

import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import seaborn as sns
import missingno as msno # 可视化工具，pip install missingno

from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.metrics import auc,roc_auc_score,roc_curve,recall_score
from sklearn.metrics import accuracy_score,classification_report

from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')

3.2、解码数据

1、加载数据

data = pd.read_csv('./creditcard.csv')
data.tail()    # 查看尾部数据
data.head()    # 查看头部数据

• 从上面可以看出，数据为结构化数据，不需要抽特征转化，但特征Time和Amount的数据规格和其他特征不一样，需要对其做特征做特征缩放。

2、数据查看

print(data.shape)
data.info()   # 查看数据分布

• 本数据集大小为28万行，31列。
• 通过查看数据信息得知，数据的类型基本是float64和int64数据类型。

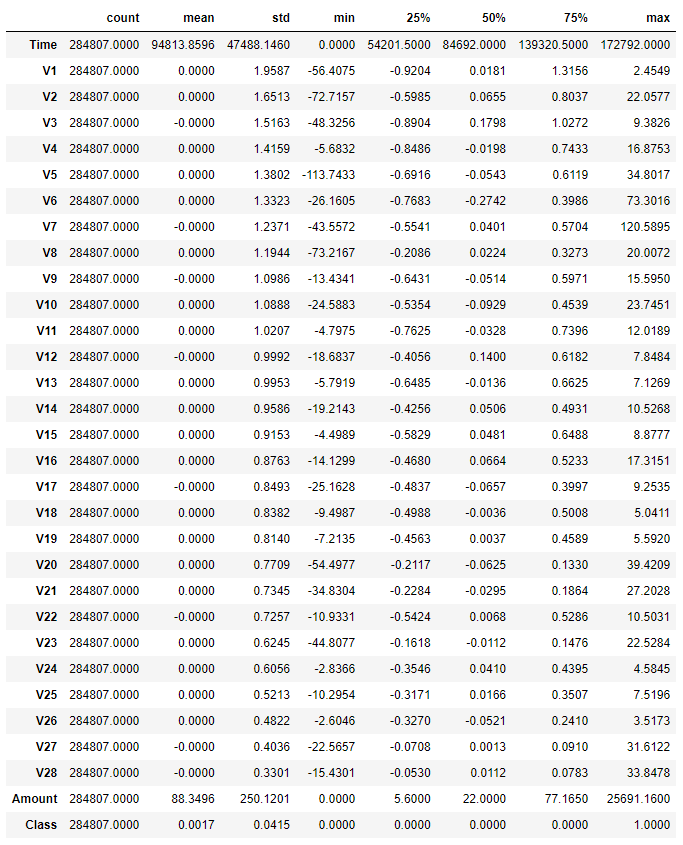
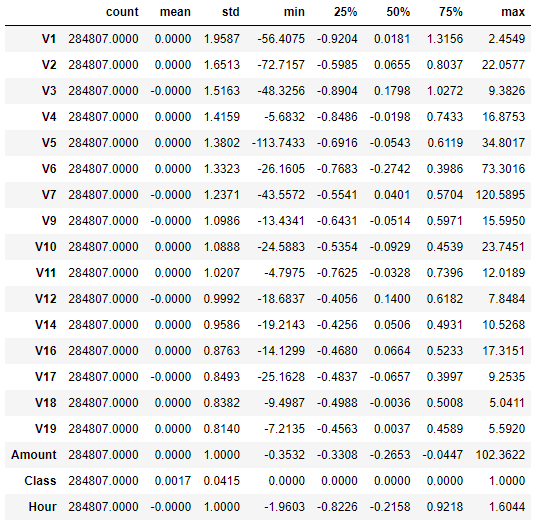
3、查看统计信息

data.describe().T      # 查看数据基本统计信息

 

• 查看数据可知，时间和金额数据相对于其他特征偏大。

4、查看缺失值

msno.matrix(data)

•  通过上图可以获知，数据集不存在缺失值，因此不需作缺失值处理。

4、特征工程

4.1、目标变量

fig,axs = plt.subplots(1,2,figsize = (14,7))

sns.countplot(x = 'Class',data = data,ax = axs[0])
axs[0].set_title('Frequency of each Calss')

data['Class'].value_counts().plot(kind = 'pie',ax = axs[1],autopct = '%1.2f%%')
axs[1].set_title('Percent of each Class')

data.groupby(by = 'Class').size()
'''Class
0    284315
1       492
dtype: int64'''

数据集284,807笔交易中有492笔是信用卡被盗刷交易，信用卡被盗刷交易占总体比例为0.17%，信用卡交易正常和被盗刷两者数量不平衡，样本不平衡影响分类器的学习，稍后我们将会使用过采样的方法解决样本不平衡的问题。

4.2、特征衍生

特征Time的单为秒，我们将其转化为以小时为单位对应每天的时间。

data['Hour'] = data['Time'].apply(lambda x : divmod(x,3600)[0])

4.3、特征选择（数据探索）

4.3.1、信用卡正常消费与被盗刷区别

XFraud = data.loc[data['Class'] == 1] # 盗刷
XnonFraud = data.loc[data['Class'] == 0] # 正常消费

correlationNonFraud = XnonFraud.loc[:,data.columns != 'Class'].corr()
mask = np.zeros_like(correlationNonFraud)
index = np.triu_indices_from(correlationNonFraud) # 右上部分的索引
mask[index] = True # mask 面具，0没有面具，1表示有面具

kw = {'width_ratios':[1,1,0.05],'wspace':0.2}
f,(ax1,ax2,ax3) = plt.subplots(1,3,gridspec_kw=kw,figsize = (22,9))

cmap = sns.diverging_palette(220,8,as_cmap = True) # 一系列颜色
sns.heatmap(correlationNonFraud,ax = ax1,vmin = -1,vmax = 1,square=False,
            linewidths=0.5,mask = mask,cbar=False,cmap= cmap)
ax1.set_title('Normal', size=24)
correlationFraud = XFraud.loc[:,data.columns != 'Class'].corr()
sns.heatmap(correlationFraud,vmin = -1,vmax= 1,cmap = cmap,ax = ax2,
            square=False,linewidths=0.5,mask = mask,yticklabels=True,cbar_ax=ax3,
           cbar_kws={'orientation':'vertical','ticks':[-1,-0.5,0,0.5,1]})

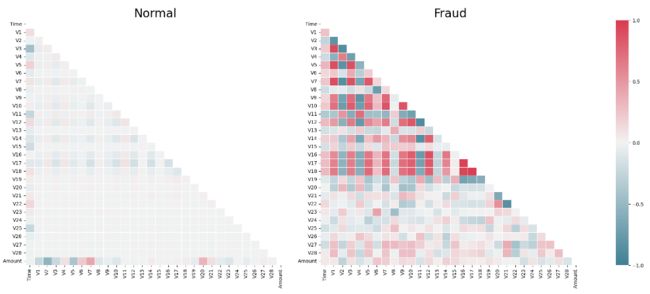
ax2.set_title('Fraud', size=24)

•  从上图可以看出，信用卡被盗刷的事件中，部分变量之间的相关性更明显。其中变量V1、V2、V3、V4、V5、V6、V7、V9、V10、V11、V12、V14、V16、V17和V18以及V19之间的变化在信用卡被盗刷的样本中呈现一定的规律。
• 特征V8、V13 、V15 、V20 、V21 、V22、 V23 、V24 、V26 、V27 和V28规律不明显！

4.3.2、交易金额和交易次数的关系

f,(ax1,ax2) = plt.subplots(2,1,sharex=True,figsize = (16,6))
ax1.hist(data['Amount'][data['Class'] == 1],bins = 30)
ax1.set_title('Fraud')
plt.yscale('log')

ax2.hist(data['Amount'][data['Class'] == 0],bins = 100)
ax2.set_title('Normal')

plt.xlabel('Amount($)')
plt.ylabel('count')
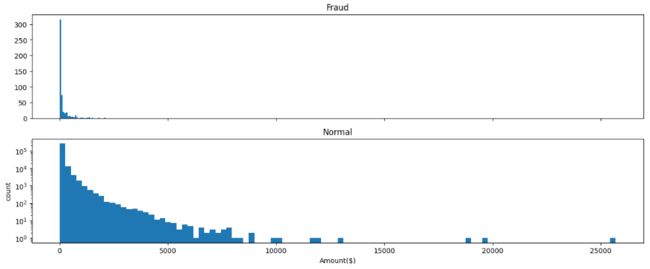
plt.yscale('log')

•  信用卡被盗刷发生的金额与信用卡正常用户发生的金额相比呈现散而小的特点，这说明信用卡盗刷者为了不引起信用卡卡主的注意，更偏向选择小金额消费。

4.3.3、信用卡消费盗刷时间分析

大家哪个时间段最爱消费？

sns.catplot(x = 'Hour',data = data,kind = 'count',palette = 'ocean',aspect = 3)

 参数介绍：

• size 每个面的高度（英寸） 标量
• aspect 纵横比 标量

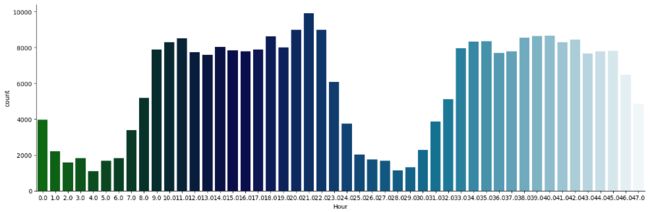
• 每天早上9点到晚上11点之间是信用卡消费的高频时间段。

4.3.4、交易金额和交易时间的关系

f,(ax1,ax2) = plt.subplots(2,1,sharex=True,figsize = (16,6))
cond1 = data['Class'] == 1
ax1.scatter(data['Hour'][cond1],data['Amount'][cond1])
ax1.set_title('Fraud')

cond2 = data['Class'] == 0
ax2.scatter(data['Hour'][cond2],data['Amount'][cond2])
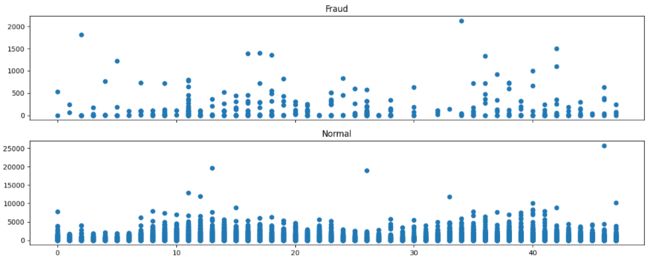
ax2.set_title('Normal')

sns.catplot(x = 'Hour',kind = 'count',data = data[cond1], height=9, aspect=2)

•  从上图可以看出，在信用卡被盗刷样本中，离群值发生在客户使用信用卡消费更低频的时间段。信用卡被盗刷数量案发最高峰在第一天上午11点达到43次，其余发生信用卡被盗刷案发时间在晚上时间11点至第二早上9点之间，说明信用卡盗刷者为了不引起信用卡卡主注意，更喜欢选择信用卡卡主睡觉时间和消费频率较高的时间点作案；同时，信用卡发生被盗刷的最大值也就只有2,125.87美元。

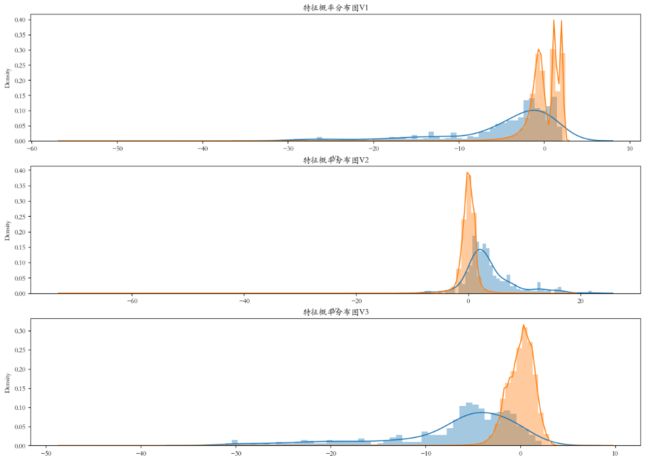
4.3.5、特征分布查看

plt.rcParams['font.family'] = 'STKaiti'
v_feat = data.iloc[:,1:29].columns
plt.figure(figsize=(16,4 * 28))
cond1 = data['Class'] == 1
cond2 = data['Class'] == 0

gs = gridspec.GridSpec(28,1) # 子视图
for i,cn in enumerate(v_feat):
    ax = plt.subplot(gs[i])
    sns.distplot(data[cn][cond1],bins = 50) # 欺诈
    sns.distplot(data[cn][cond2],bins = 100) # 正常消费
    ax.set_title('特征概率分布图' + cn)

• 上图是不同变量在信用卡被盗刷和信用卡正常的不同分布情况，我们将选择在不同信用卡状态下的分布有明显区别的变量。因此剔除变量V8、V13 、V15 、V20 、V21 、V22、 V23 、V24 、V25 、V26 、V27 和V28变量。这也与我们开始用相关性图谱观察得出结论一致。同时剔除变量Time，保留离散程度更小的Hour变量。
• 当在该特征下, 盗刷和正常的数据分布没有差别时, 该特征意义不大。

droplist = ['V8','V13','V15','V20','V21','V22','V23','V24',
            'V25','V26','V27','V28','Time']
data_new = data.drop(labels=droplist,axis = 1)
display(data.shape, data_new.shape)

• 特征从31个缩减至18个（不含目标变量）。

4.4、特征缩放

由于特征 Hour 和 Amount 的规格和其他特征相差较大，因此我们需对其进行特征缩放。

col = ['Amount','Hour']
sc = StandardScaler()       # Z-score归一化
data_new[col] = sc.fit_transform(data_new[col])
data_new.head()

data_new.describe().T

4.5、特征重要性

1、构建X变量和y变量

feture = list(data_new.columns)
feture.remove('Class') # 特征名，修改原数据
X = data_new[feture]
y = data_new['Class']
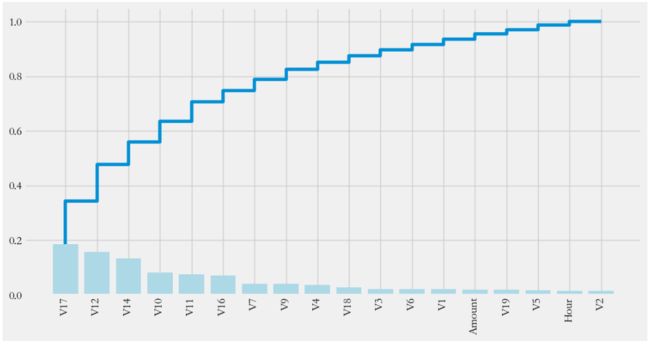
display(X.head(),y.head())

2、利用随机森林的feature importance对特征的重要性进行排序

from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()
clf.fit(X,y)
clf.feature_importances_

plt.rcParams['figure.figsize'] = (12,6)
plt.style.use('fivethirtyeight')

importances = clf.feature_importances_
feat_name = feture
feat_name = np.array(feat_name)
index = np.argsort(importances)[::-1]

plt.bar(range(len(index)),importances[index],color = 'lightblue')
plt.step(range(18),np.cumsum(importances[index]))
_ = plt.xticks(range(18),labels=feat_name[index],rotation = 'vertical',
               fontsize = 14)

5、模型训练

5.1、过采样

前面提到，目标列Class呈现较大的样本不平衡，会对模型学习造成困扰。样本不平衡常用的解决方法有过采样和欠采样，本项目处理样本不平衡采用的是过采样的方法，具体操作使用 SMOTE （SyntheticMinority Oversampling Technique）

# 构建自变量和因变量
feature = list(data_new.columns)
feature.remove('Class')

X = data[feature]
y = data["Class"]
n_sample = y.shape[0]
n_pos_sample = y[y == 0].shape[0]
n_neg_sample = y[y == 1].shape[0]
print('样本个数：{}; 正样本占{:.2%}; 负样本占{:.2%}'.format(n_sample,
                                               n_pos_sample / n_sample,
                                               n_neg_sample / n_sample))
print('特征维数：', X.shape[1])  # 特征维数： 18
# 样本个数：284807; 正样本占99.83%; 负样本占0.17%

• 处理不平衡数据

# pip install imblearn
from imblearn.over_sampling import SMOTE # 近邻规则，创造一些新数据
smote = SMOTE()
# X，y是数据
X,y = smote.fit_resample(X,y)
print('在过采样之后样本比例是：\n',y)   # 0: 284315     1: 284315

• 通过SMOTE方法平衡正负样本后
• 样本个数：568630; 正样本占50.00%; 负样本占50.00%

5.2、算法建模

1、准确率

model = LogisticRegression()
model.fit(X,y) # 样本是均衡的
y_ = model.predict(X)
print('逻辑斯蒂回归算准确率是：',accuracy_score(y,y_))   #  0.9590348732919474
# 信用卡反欺诈，更希望算法，找到盗刷的交易！

2、混淆矩阵与召回率

from sklearn.metrics import confusion_matrix  # 混淆矩阵
cm = confusion_matrix(y,y_)
print(cm)
recall = cm[1,1]/(cm[1,1] + cm[1,0])
print('召回率：',recall)    # 0.9325009232717233

def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    绘制预测结果与真实结果的混淆矩阵
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")
    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

import itertools
plot_confusion_matrix(cm,classes=[0,1])

 3、ROC与AUC

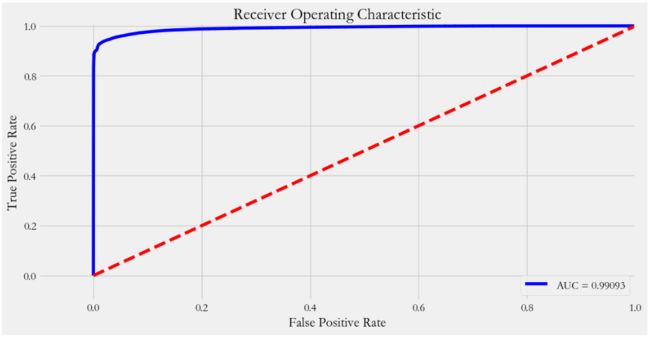
proba_ = model.predict_proba(X)[:,1]  # 索引1，表示获取类别1的概率，正样本
fpr,tpr,thesholds_ = roc_curve(y,proba_)
roc_auc = auc(fpr,tpr) # 曲线下面积

# 绘制 ROC曲线
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b',label='AUC = %0.5f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.0])
plt.ylim([-0.1,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')

 6、模型评估与优化

上一个步骤中，我们的模型训练和测试都在同一个数据集上进行，这样导致模型产生过拟合的问题。一般来说，将数据集划分为训练集和测试集有3种处理方法：

• 留出法（hold-out）
• 交叉验证法（cross-validation）
• 自助法（bootstrapping）

本次项目采用的是交叉验证法划分数据集，将数据划分为3部分：训练集（training set）、验证集
（validation set）和测试集（test set）。让模型在训练集进行学习，在验证集上进行参数调优，最后使用测试集数据评估模型的性能。
模型调优我们采用网格搜索调优参数（grid search），通过构建参数候选集合，然后网格搜索会穷举各种参数组合，根据设定评定的评分机制找到最好的那一组设置。
结合cross-validation和grid search，具体操作我们采用scikit learn模块model_selection中的
GridSearchCV方法。

6.1、交叉验证

1、交叉验证模型训练（训练时间稍长）

%%time
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

# 构建参数组合
param_grid = {'C': [0.01,0.1, 1, 10, 100, 1000,],'penalty': [ 'l1', 'l2']}
# 确定模型LogisticRegression，和参数组合param_grid ，cv指定10折
grid_search = GridSearchCV(LogisticRegression(),param_grid,cv=10) 
grid_search.fit(X_train, y_train) # 使用训练集学习算法

2、最有参数查看

results = pd.DataFrame(grid_search.cv_results_)
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.5f}".format(grid_search.best_score_))
'''
Best parameters: {'C': 0.1, 'penalty': 'l2'}
Best cross-validation score: 0.95890  '''

3、测试数据评估

y_pred = grid_search.predict(X_test)
print("Test set accuracy score: {:.5f}".format(accuracy_score(y_test, y_pred)))
'''
Test set accuracy score: 0.95874  '''

4、分类效果评估报告

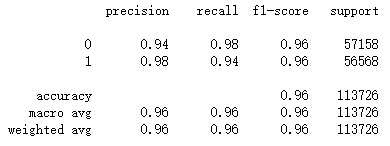
from sklearn.metrics import classification_report
print(classification_report(y_test,y_pred))

6.2、混淆矩阵

# 生成测试数据混淆矩阵
cnf_matrix = confusion_matrix(y_test, y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ",     # 0.9353874982322161
      cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# 绘制模型优化后的混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
                      classes=class_names,
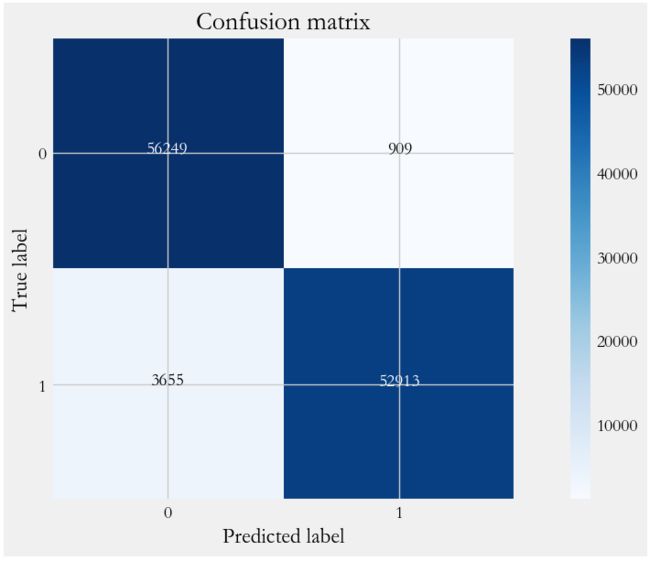
                      title='Confusion matrix')

# 生成全部数据混淆矩阵
y_ = grid_search.predict(X) # 优化后的算法，最佳参数C：10，pentaly：l2
cnf_matrix = confusion_matrix(y, y_)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ",    # 0.9352865659567733
      cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# 绘制模型优化后的混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, 
                      classes=class_names,
                      title='Confusion matrix')

• 从上可以看出，经过交叉验证训练和参数调优后，模型的性能有较大的提升，recall值从0.818上升到0.9318，上升幅度达到11.34%。

6.3、模型评估

解决不同的问题，通常需要不同的指标来度量模型的性能。例如我们希望用算法来预测癌症是否是恶性的，假设100个病人中有5个病人的癌症是恶性，对于医生来说，尽可能提高模型的查全率（recall）比提高查准率（precision）更为重要，因为站在病人的角度，发生漏发现癌症为恶性比发生误判为癌症是恶性更为严重。

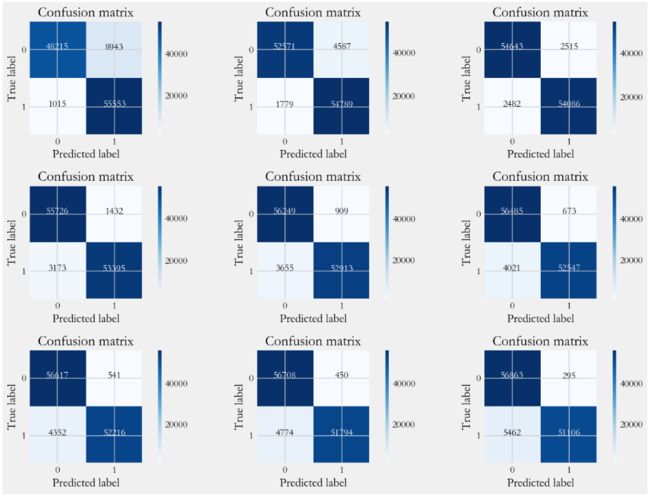
6.3.1、混淆矩阵

# 获得预测概率值
y_pred_proba = grid_search.predict_proba(X_test) 

thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]  # 设定不同阈值

plt.figure(figsize=(15,10))
np.set_printoptions(precision=2)
j = 1
for t in thresholds:
    # 根据阈值转换为类别 
    y_pred = y_pred_proba[:,1] > t
    plt.subplot(3,3,j)
    j += 1
    # 计算混淆矩阵
    cnf_matrix = confusion_matrix(y_test, y_pred)
    print("召回率:",cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]),end='\t')
    print('准确率:',(cnf_matrix[0,0] + cnf_matrix[1,1])/(cnf_matrix.sum()))
    # 绘制混淆矩阵
    class_names = [0,1]
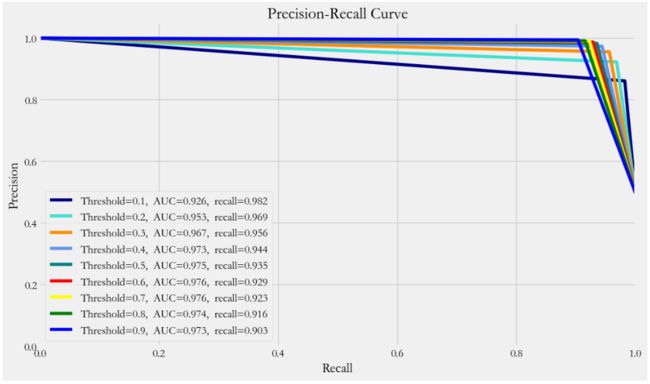
    plot_confusion_matrix(cnf_matrix, classes=class_names)

6.3.2、精确率-召回率曲线

from sklearn.metrics import precision_recall_curve
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
colors = ['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal', 'red', 
          'yellow', 'green', 'blue']

plt.figure(figsize=(12,7))

j = 1
for t,color in zip(thresholds,colors):
    y_pred = y_pred_proba[:,1] > t #预测出来的概率值是否大于阈值  

    precision, recall, threshold = precision_recall_curve(y_test, y_pred)
    area = auc(recall, precision)
    cm = confusion_matrix(y_test,y_pred)
    # TP/(TP + FN)
    r = cm[1,1]/(cm[1,0] + cm[1,1])
  
    # 绘制 Precision-Recall curve
    plt.plot(recall, precision, color=color,
                 label='Threshold=%s,  AUC=%0.3f,  recall=%0.3f' %(t,area,r))
    plt.xlabel('Recall')
    plt.ylabel('Precision')
    plt.ylim([0.0, 1.05])
    plt.xlim([0.0, 1.0])
    plt.title('Precision-Recall Curve')
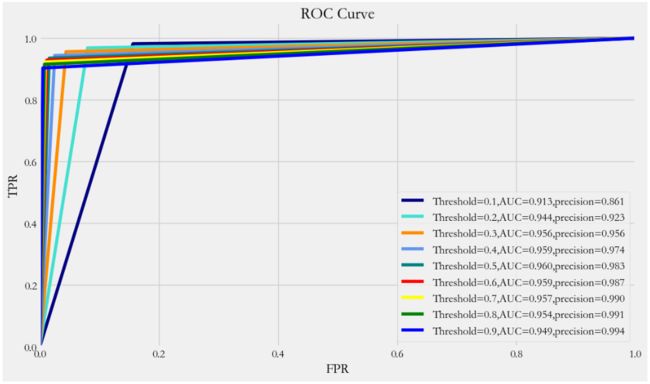
    plt.legend(loc="lower left")

 6.3.3、ROC曲线

thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
colors = ['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal', 'red',
          'yellow', 'green', 'blue']

plt.figure(figsize=(12,7))

j = 1
for t,color in zip(thresholds,colors):
#     y_pred = grid_search.predict(X_teste) # 算法预测测试数据的值
    y_pred = y_pred_proba[:,1] >= t #预测出来的概率值是否大于阈值 （人为） 
  
    cm = confusion_matrix(y_test,y_pred)
    # TP/(TP + FP)
    precision = cm[1,1]/(cm[0,1] + cm[1,1])

    fpr,tpr,_ = roc_curve(y_test,y_pred)
    accuracy = accuracy_score(y_test,y_pred)
  
    auc_ = auc(fpr,tpr)
  
    # 绘制 ROC curve
    plt.plot(fpr, tpr, color=color,
             label='Threshold=%s,AUC=%0.3f,precision=%0.3f' %(t, auc_,precision))
    plt.xlabel('FPR')
    plt.ylabel('TPR')
    plt.ylim([0.0, 1.05])
    plt.xlim([0.0, 1.0])
    plt.title('ROC Curve')
    plt.legend(loc="lower right")

6.3.4、各评估指标趋势图

'''
true negatives:`C_{0,0}`
false negatives: `C_{1,0}` 
true positives is:`C_{1,1}` 
false positives is :`C_{0,1}`
'''
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
recalls = [] # 召回率
precisions = [] # 精确度
aucs = [] # 曲线下面积
y_pred_proba = grid_search.predict_proba(X_test)
for threshold in thresholds:
    y_ = y_pred_proba[:,1] >= threshold
    cm = confusion_matrix(y_test,y_)
    # TP/(TP + FN)
    recalls.append(cm[1,1]/(cm[1,0] + cm[1,1])) 
    # 召回率，从真的癌症患者中找出来的比例，200,85个，42.5%
    # TP/(TP + FP)
    precisions.append(cm[1,1]/(cm[0,1] + cm[1,1])) 
    # 精确率，找到癌症患者，100个，85个真的，15个没病，预测有病
    fpr,tpr,_ = roc_curve(y_test,y_)
    auc_ = auc(fpr,tpr)
    aucs.append(auc_)
    
plt.figure(figsize=(12,6))
plt.plot(thresholds,recalls,label = 'Recall')
plt.plot(thresholds,aucs,label = 'auc')
plt.plot(thresholds,precisions,label = 'precision')
plt.legend()
plt.xlabel('thresholds')

6.4、最优阈值

precision和recall是一组矛盾的变量。从上面混淆矩阵和PRC曲线、ROC曲线可以看到，阈值越小，recall值越大，模型能找出信用卡被盗刷的数量也就更多，但换来的代价是误判的数量也较大。随着阈值的提高，recall值逐渐降低，precision值也逐渐提高，误判的数量也随之减少。通过调整模型阈值，控制模型反信用卡欺诈的力度，若想找出更多的信用卡被盗刷就设置较小的阈值，反之，则设置较大的阈值。
实际业务中，阈值的选择取决于公司业务边际利润和边际成本的比较；当模型阈值设置较小的值，确实能找出更多的信用卡被盗刷的持卡人，但随着误判数量增加，不仅加大了贷后团队的工作量，也会降低误判为信用卡被盗刷客户的消费体验，从而导致客户满意度下降，如果某个模型阈值能让业务的边际利润和边际成本达到平衡时，则该模型的阈值为最优值。当然也有例外的情况，发生金融危机，往往伴随着贷款违约或信用卡被盗刷的几率会增大，而金融机构会更愿意不惜一切代价守住风险的底线。