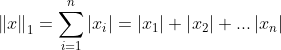【应用】【正则化】L1、L2正则化

L1正则化的作用：特征选择从可用的特征子集中选择有意义的特征，化简机器学习问题。著名的LASSO（Least Absolute Shrinkage and Selection Operator）模型将L1惩罚项和线性模型结合，使用最小二乘代价函数。L1正则化导致模型参数的稀疏性，被广泛地用于特征选择（feature selection）机制。

L2正则化的作用：PRML书中描述“focus on quadratic both for its practical importance and analytical tractbility”，即L2正则化具有实际应用的重要性和分析的易处理性。

接下来的博文，以L1、L2及Lp范数为开篇，介绍多种范数的数学表达式和几何轮廓。其次，描述线性回归的代价函数中正则化的作用；最后以几何图形的方式，描述L1和L2正则化对模型稀疏性的影响。

目录

一、范数及几何轮廓

二、正则化最小二乘估计

三、L1、L2正则化直观理解

---

一、范数及几何轮廓

L1正则化和L2正则化（L1，L2 Regularization）使用的正则化项是L1范数和L2范数[3]。换个角度来看，L1和L2范数是Lp范数的特殊形式。

Lp范数：

L2范数：

L1范数：

当我们的目标是二维优化时，L0.5、L1、L2、L3、L4的几何轮廓如下图所示。由图可知，p的值越小，几何轮廓越贴近坐标轴；p的值越大，几何轮廓越远离坐标轴。

 绘制上图采用的半径为1，代码如下：

import numpy as np
import matplotlib.pyplot as plt
import math

norm_list = [0.5, 1, 2, 3, 4]
plt.figure(figsize=(5 * len(norm_list), 4 * 1))

for index, value in enumerate(norm_list):

    y = 1.0
    w1 = [i for i in np.arange(-1.0, 1.0, 0.0001)]
    # 当w2 >= 0时：
    w2_positive = [math.pow(y - abs(j) ** value, 1 / value) for j in w1]
    # 当w2 < 0时：
    w2_negative = [-1 * math.pow(y - abs(j) ** value, 1 / value) for j in w1]
    # 所有点集
    w1_all = w1 + w1
    w2_all = w2_positive + w2_negative
    plt.subplot(1, len(norm_list), index+1)
    plt.plot(w1_all, w2_all, '.', alpha=0.5)
    plt.title(f"L{value}-norm")
    plt.xlabel("w1")
    plt.ylabel("w2")
    
plt.subplots_adjust(wspace=0.5, hspace=0)
plt.show()

二、正则化最小二乘估计

为了防止过拟合，我们通常会在目标函数中加上正则化项：

式中：

是与数据和参数相关的损失函数；

是与参数相关的正则化项。

如果我们对损失函数添加二范数的正则化项，得到：

使用最小二乘估计法，让 cost function 对W求偏导，可求得W*：

上式中每个符号代表的含义请查阅文献[1]，这里不作过多的阐述。

三、L1、L2正则化直观理解

L1范数的正则化又称为lasso，它有个特性是：当足够大时，部分系数会趋近于0，从而导致模型出现稀疏性。L2范数的正则化又称为ridge，但稀疏性特点在L2范数下的正则化时会得到改善。

深入的来看，当我们想最小化cost function时，假定的最大值为，即：

那么，cost function的最小化问题等价于在约束  下最小化非正则化项 。

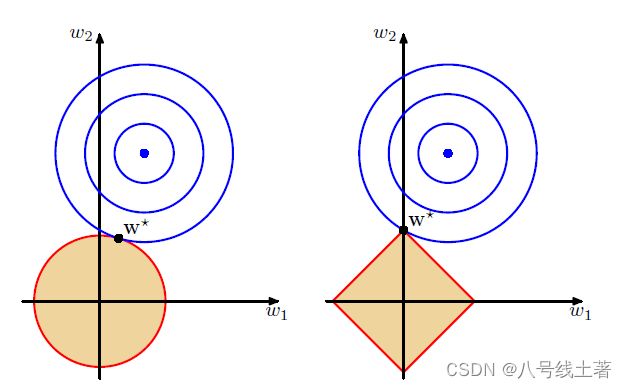
lasso和ridge稀疏性的变化可通过二维平面来直观理解：

 阴影区域是惩罚项L2和L1的参数空间；蓝色线条是的等值线。当w1和w2在参数空间内寻找最优解时，蓝色区域会不断扩大，当与阴影区域第一次相切时为最优解 W*。但是，不同点在于L2的最优解W*不是在拐点处取得，而L1的最优解会在拐角处（0，w2）取得。那么在高维空间内，除了拐点以外，还有很多边的轮廓取得最优解，这又会产生更多的稀疏性。所以，L1正则化多用于特征选择，L2正则化多用于抑制过拟合。

参考文献：

[1] Christopher M, Bishop F.R.Eng. Pattern Recognition and Machine Learning[M]. Springer, 2006.

[2] Ian Godfellow, Yosua Bengio, Aaron Courville. Deep Learning[M]. MIT Press, 2017.

[3] 天池平台. 阿里云天池大赛赛题解析[M]. 电子工业出版社, 2020.