从FPGA说起的深度学习(三)
这是新的系列教程,在本教程中,我们将介绍使用 FPGA 实现深度学习的技术,深度学习是近年来人工智能领域的热门话题。
在本教程中,旨在加深对深度学习和 FPGA 的理解。
用 C/C++ 编写深度学习推理代码
高级综合 (HLS) 将 C/C++ 代码转换为硬件描述语言
FPGA 运行验证

在上一篇文章中,我们在 MNIST 数据集上创建并训练了一个网络模型。从本文开始,为了在 FPGA 上运行推理处理,我们将首先用 C++ 编写推理处理代码。
在这篇 C++ 实现的第一篇文章中,我们开始针对卷积层的 C++ 实现。具体内容是(1)卷积层的实现,(2)运算校验(C验证,C/RTL协同验证)(就是HLS的流程)。
卷积层实现
在上一篇文章中,我解释了卷积层是对图像的过滤过程,但是并没有解释输入输出通道如何处理,过滤时图像的边缘处理等。由于本文旨在实现层面的理解,因此我将详细介绍这些要点。
处理 I/O 通道
在图像处理中,对RGB输入图像进行噪声去除等滤波处理,并频繁地进行RGB图像的处理。在这种情况下,卷积过程往往是针对每个通道(R/G/B)独立完成的,输入的G/B通道值不影响输出的R通道结果。
 每通道独立卷积
每通道独立卷积
另一方面,在卷积层中执行的卷积过程中,所有输入通道的值影响每个输出通道。因此,对于输出图像的每个像素(输出通道,Y坐标,X坐标),所有输入通道和周围的像素区域都会参与计算,导致计算量非常大。
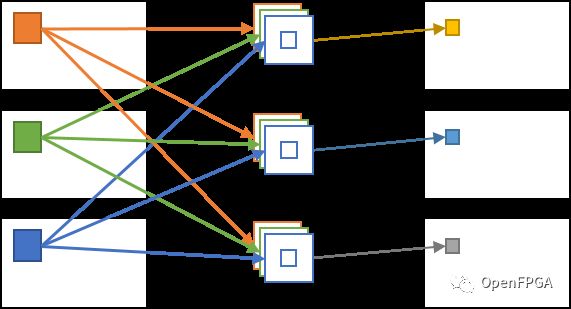 使用所有通道的卷积
使用所有通道的卷积
另外,如上所述每个通道独立卷积的卷积层称为Depthwise Convolution。
这通常用于减少计算量的网络模型,例如MobileNet(https://arxiv.org/abs/1704.04861)。
图像边缘处理
在对图像进行卷积处理时,图像边缘的处理往往是一个问题。
由于卷积过程在计算某个像素时使用了周围像素,因此对于没有周围像素的像素,例如图像边缘的像素,就无法获取周围像素。
卷积神经网络主要通过以下两种方式处理边缘像素。
无填充:输出图像减少了输入图像的卷积区域。
补零:将输入图像预先用卷积区域扩展,用零填充该区域,对原始输入图像进行卷积处理。
没有填充的卷积的图形表示如下所示:在这种情况下,输出图像将是比输入图像小一个滤波器尺寸的区域(橙色部分)。如果内核大小为 3(中心像素 +/-1),则输出图像大小在宽度和高度上都将为 -2,因为图像之外的 1 个像素是无法进行卷积的区域。
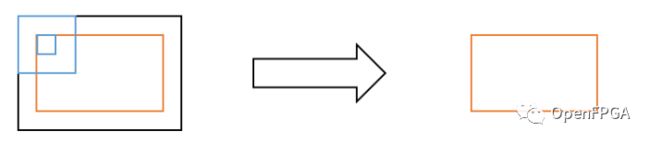 无填充卷积:输出图像缩小
无填充卷积:输出图像缩小
接下来,零填充的图形表示如下所示。在这个例子中,预先在输入图像的外部添加了一个值为0的区域(灰色区域),进行卷积,这样就不会出现图像缩小现象。如果内核大小为 3,则带填充的输入图像大小在宽度和高度上均为 +2,因为 +1 像素将添加到屏幕外部且值为零。
 零填充卷积:输出图像大小保持不变
零填充卷积:输出图像大小保持不变
在我们的模型中,我们在所有卷积层中使用零填充。
C代码
如果根据目前为止的解释用 C 语言实现卷积过程,它将类似于下面的代码。
void conv2d(const float* x, const float* weight, const float* bias, int32_t width, int32_t height,
int32_t in_channels, int32_t out_channels, int32_t ksize, float* y) {
for (int32_t och = 0; och < out_channels; ++och) {
for (int32_t h = 0; h < height; ++h) {
for (int32_t w = 0; w < width; ++w) {
float sum = 0.f;
for (int32_t ich = 0; ich < in_channels; ++ich) {
for (int32_t kh = 0; kh < ksize; ++kh) {
for (int32_t kw = 0; kw < ksize; ++kw) {
int32_t ph = h + kh - ksize/2;
int32_t pw = w + kw - ksize/2;
// zero padding
if (ph < 0 || ph >= height || pw < 0 || pw >= width) {
continue;
}
int64_t pix_idx = (ich * height + ph) * width + pw;
int64_t weight_idx = ((och * in_channels + ich) * ksize + kh) * ksize + kw;
sum += x[pix_idx] * weight[weight_idx];
}
}
}
// add bias
sum += bias[och];
y[(och * height + h) * width + w] = sum;
}
}
}
}此函数的解释如下所示:
输入
-- x: 输入图像。shape=(in_channels, height, width)
-- weight: 权重因子。shape=(out_channels, in_channels, ksize, ksize)
-- bias: 偏置值。shape=(out_channels)
输出
-- y: 输出图像。shape=(out_channels, height, width)
参数:-- width: 输入/输出图像的宽度
-- height: 输入/输出图像高度
-- in_channels:输入图像的通道数
-- out_channels:输出图像的通道数
-- ksize: 内核大小
每个输入/输出的内存布局shape=(...)如表格所示,但float x[in_channels][height][width];将其视为定义为三维数组。
卷积层的处理是一个6级循环。第一个三级循环确定输出图像上的位置,随后的三级循环对该位置执行卷积操作。
零填充在第 24-26 行完成。由于实际创建零填充输入图像是低效的,所以零填充是通过在访问图像外部时不参与乘积之和来实现的。
第31行是卷积过程中的积和运算部分,这个积和运算out_channels * height * width * in_channels * ksize * ksize进行了两次。这个卷积过程的操作数量非常大,在很多情况下,卷积层支配着卷积神经网络的执行时间。这就是为什么计算单元比 CPU 多的 GPU 和 FPGA 更适合处理神经网络。
第37行是偏差处理部分。到目前为止,我还没有触及什么是偏差处理,但正如我在这里所写的那样,它是一个简单地对输出值进行偏移的过程。这种偏差处理在输入通道/内核大小 (Y,X) 循环之外,因此处理步骤的数量非常微不足道。
运算检查
作为对上一节创建的函数运行的确认,conv2d我们将比较结果是否足够接近在 PyTorch 的 C++ API (libtorch) 上执行的卷积计算。
每个测试包括以下两个步骤。
C. 验证
C/RTL 协同验证
1、C 验证类似于正常的软件开发,gcc只是用通用的编译器编译源代码并检查结果。
2、C/RTL协同验证是使用AMD-Xilinx提供的高阶综合工具Vitis HLS进行验证。对于此验证,HLS 首先将 C 源代码转换为 Verilog HDL 等 RTL。然后在 Vivado 中对生成的 RTL 执行功能仿真。
在这个逻辑仿真中,将一个类似于C验证的数据序列输入到创建的电路中,确认输出结果是否正确。
本节以后的内容将以运行创建的源代码的形式进行说明。
源代码将在后面发布。
运行环境
运行环境面向 Linux 机器。不支持 Windows/Mac 操作系统。此外,由于预装gcc版本,该发行版针对 Ubuntu 18.04。难以自行准备运行环境的朋友,看看就行。
需要以下工具。
Vivado 2020.2(推荐 2019.2)
cmake >= 3.11
cmake比较麻烦,因为它需要的版本比apt等包管理器可以安装的版本高,但是可以下载预构建的二进制文件(cmake--Linux-x86_64.tar.gz)。
C. 验证
测试代码/tests/ref/conv2d.cc的使用,我不会在本文中详细介绍,但测试将是一个正常的随机测试。
可以按照以下步骤构建代码。请将 -DVIVADO_HLS_ROOT 的值相应地替换为安装的 Vivado 的路径。
$ mkdir /build
$ cd /build
$ cmake .. -DVIVADO_HLS_ROOT=/tools/Xilinx/Vivado/2022.2
$ cmake --build . 使用以下命令进行测试:如果没有任何错误,那它就是成功的。
$ ctest -V -R "conv2d_ref"C/RTL 协同验证
运行以下命令以使用 HLS 启动 C/RTL 协同验证。大约需要 5 分钟。
$ ctest -V -R "conv2d_hls_cosim"当执行 C/RTL 协同验证时,会自动创建一个 HLS 项目文件,因此可以使用它来检查高级综合和 RTL 仿真波形的结果。
要检查这一点,请使用以下命令启动 HLS:
$ vitis_hls &HLS 打开后,单击“打开项目”,如下所示,导航到/build/tests/hls/conv2d/conv2d_hls_cosim目录并单击“确定”。
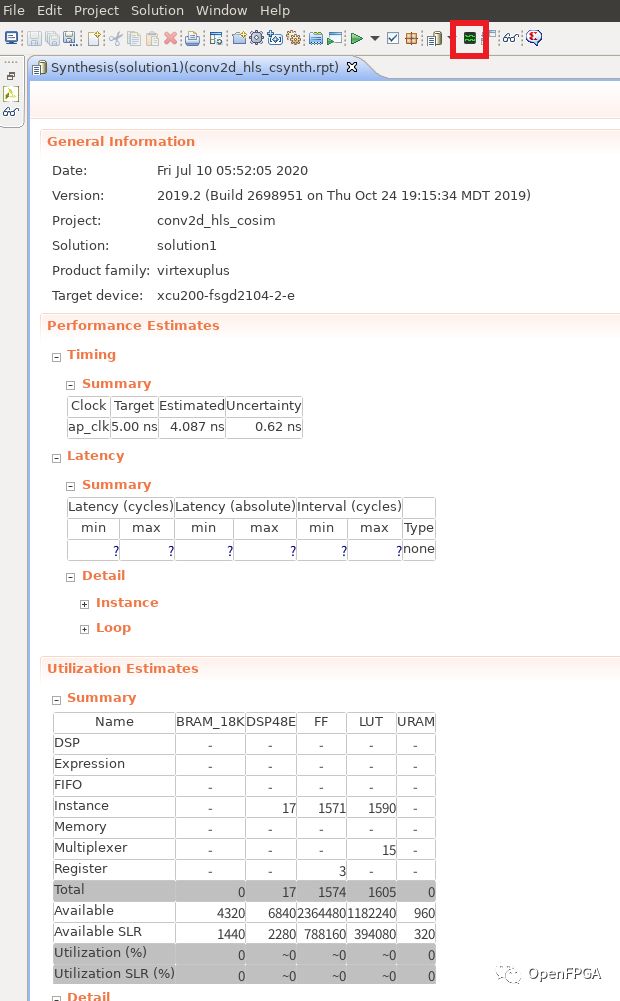
然后,HLS 综合报告将显示如下屏幕所示。
从此报告中,可以看到从 Performance Estimates 列创建的电路的估计性能,以及从 Utilization Estimates 看到在目标设备上实施时的估计资源使用情况。
点击顶部红框包围的区域,可以看到仿真的波形。
波形如下所示,可以看出可以通过某种方式读取到该值,大概2000.00ns就能输出y的第一个值。

通过这种方式,我们能够创建一个逻辑电路,该逻辑电路使用 HLS 执行卷积层计算,而无需特别注意 HW。
然而,由于这个电路根本没有调整,它的设计只是实现功能,在后续会对此进行优化。
总结
在这篇文章中,用 C++ 实现了一个卷积层并确认了它的运行。我们还在这个 C++ 实现上使用 HLS 进行了高级综合,并确认它在 C/RTL 协同验证中没有任何问题。
在下一篇文章中,我们将用 C++ 实现其余两层(池化层、全连接层)和 ReLU。之后,我们会结合所有实现的层,为MNIST创建和验证一个模型。
