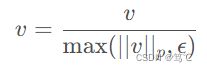【Python--torch.nn.functional】F.normalize用法 + 代码说明

【Python–torch.nn.functional】F.normalize介绍 + 代码说明

1. 介绍

import torch.nn.functional as F
F.normalize(input: Tensor, p: float = 2.0, dim: int = 1, eps: float = 1e-12) -> Tensor

• input: 是一个任意维度的Tensor类型的数据
• p：默认为2，表示2范数；同理，p=1表示1范数
• dim：
  • 默认为1，在输入数据input的shape是二维的且p=2情况下，表示对行进行操作，即所有元素除以第一行元素的根号下平方和；
  • dim=0 时，在输入数据input的shape是二维的且p=2情况下，表示对列进行操作，即所有元素除以第一列元素的根号下平方和；
  • dim为其他值时，之后通过代码分析。
• eps：默认为1e-12，防止除0。

因此，Normalize对应的公式为：

2. 代码说明

2.1 一维Tensor

c = torch.Tensor([1, 2, 3])
print(F.normalize(c, dim=0))
'''
tensor([0.2673, 0.5345, 0.8018])
torch.Size([3])
解释：
默认dim=1，是按行操作，但是一维的Tensor是列向量，所以必须指定dim=0
默认p=2，所以这个一维的Tensor（列向量）每个元素都除以sqrt(1**2 + 2**2 + 3**2)
'''

2.2 二维Tensor

import torch.nn.functional as F
import torch

a = torch.arange(20, dtype=torch.float).reshape(4,5)
b = F.normalize(a, dim=0)
c = F.normalize(a, dim=1)
print(a)
print(b)
print(c)

输出：

# 输入的数组
tensor([[ 0.,  1.,  2.,  3.,  4.],
        [ 5.,  6.,  7.,  8.,  9.],
        [10., 11., 12., 13., 14.],
        [15., 16., 17., 18., 19.]])
# dim=0时，即沿第一维度(列)做归一化
tensor([[0.0000, 0.0491, 0.0907, 0.1261, 0.1564],
        [0.2673, 0.2949, 0.3175, 0.3363, 0.3519],
        [0.5345, 0.5406, 0.5443, 0.5464, 0.5474],
        [0.8018, 0.7864, 0.7711, 0.7566, 0.7430]])
# dim=1时，即沿第二维度(行)做归一化
# 维度记忆技巧:最后一个维度始终是行，从后向前推:行、列、通道
tensor([[0.0000, 0.1826, 0.3651, 0.5477, 0.7303],
        [0.3131, 0.3757, 0.4384, 0.5010, 0.5636],
        [0.3701, 0.4071, 0.4441, 0.4812, 0.5182],
        [0.3932, 0.4195, 0.4457, 0.4719, 0.4981]])

2.3 三维Tensor

a = torch.Tensor([[[1, 2, 3], 
				   [4, 5, 6]], 
				  [[10, 20, 30], 
				   [40, 50, 60]]]) # (2, 2, 3)

print(F.normalize(a))  # dim = 1, 举个例子，1、4为1组，进行norm。

print(F.normalize(a, dim=0))  # dim = 0, 1、10为1组，进行norm。

print(F.normalize(a, dim=2)) # dim = 2, 1、2、3为1组，进行norm。

'''
tensor([[[0.2425, 0.3714, 0.4472],
         [0.9701, 0.9285, 0.8944]],

        [[0.2425, 0.3714, 0.4472],
         [0.9701, 0.9285, 0.8944]]])

tensor([[[0.0995, 0.0995, 0.0995],
         [0.0995, 0.0995, 0.0995]],

        [[0.9950, 0.9950, 0.9950],
         [0.9950, 0.9950, 0.9950]]])

tensor([[[0.2673, 0.5345, 0.8018],
         [0.4558, 0.5698, 0.6838]],

        [[0.2673, 0.5345, 0.8018],
         [0.4558, 0.5698, 0.6838]]])
'''

3. 总结

• 按照指定Tensor最大的dim的去norm时，就是对物理存储地址挨着最紧密的那一维进行norm。
• 当dim为2，此时dim最大，就是对1、2、3（物理存储地址最紧密）为一组进行norm。
• 当dim为1，则降一维度，对物理存储地址次紧密的元素为一组进行norm。也就是1、4为一组。
• 当dim为0，就是按照最远的一组。