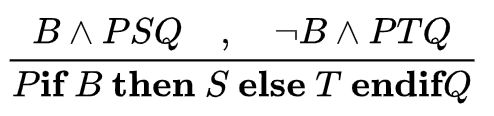浅谈程序分析

孙军 新加坡管理大学教授，研究方向为：形式化方法、软件工程、安全等，爱好：爬山、攀岩等。

如果读者想了解更多有关程序分析相关的技术内容，欢迎加入编程语言技术社区 SIG-程序分析。

加入方式：文末有小助手微信，添加并备注加入 SIG-程序分析。

---

目录

# 引言 #

# 程序分析很难! #

# 知道什么是程序正确性很难！

# 程序分析技术很多! #

# 自动定理证明

## 如何用逻辑表达

## 举个栗子

## 小结

# 抽象解释

## 如何选择适合的抽象域

## 举个栗子

## 小结

# 其他常见的方法

# 当前程序分析研究领域浅析 #

# 总结 #

---

# 引言 #

程序分析是以某种语言书写的程序为对象，对其内部的运作流程进行分析，自动分析计算程序的正确性以及高效性等属性的过程。

虽然经过了几十年的发展，程序分析仍是一个持续热门的研究领域。由于现代软件的复杂性，大型程序的正确性、性能和安全性等都面临新的挑战，所以程序分析技术不只在学术界被大批学者研究，近些年来也越来越受到企业界的青睐。随着大型软件企业逐渐意识到程序分析的重要性，投入做程序分析的公司也越来越多，如 Microsoft、Google、Apple、Facebook 和华为等都有研发团队从事程序分析工作，以及我们熟知的 Coverity、Semmle 等，此外，国内也涌现出很多做程序分析相关的企业如思码逸 Merico、鸿渐 RedRocket、鉴释 Xcalibyte、源伞 SourceBrella 等。

程序分析主要关注两大方面：

• 程序优化侧重于提高程序的性能，通过对程序中关键函数的跟踪或者运行时信息的统计，找到系统性能的瓶颈，从而采取进一步行动对程序进行优化，同时减少资源使用。
• 程序正确性侧重于确保程序执行它应该做的事情，帮助开发者找出错误代码的位置。（本文以程序正确性的分析为主）

自图灵祖师爷开天辟地以来，怎么保证程序的正确性就一直是一个老大难问题。无数大牛们尝试了各种方法来解决这个问题，结局是各种幻灭。但与此同时，这也造就了现在各种程序分析技术以及产品百花齐放的局面。本文就几种常见程序分析技术及其由来进行了简单的介绍，希望能帮助大家对程序分析有一个初步的了解。

# 程序分析很难! #

计算机发展早期，程序很简单，程序的正确性需求（specification）也很简单，因此，程序的正确性常常显而易见，或者很容易被手动证明。

自然而然地，大家就产生了一种幻觉，可能我们只需要说明我们想要满足什么样的需求，就可以根据需求自动地生成一个程序。如果这样可行的话，程序员的工作无疑将变得轻松无比。换句话讲，我们希望找到一个万能的程序。即，给定任意的需求，这个程序都能自动的生成一个特定的程序来满足需求。

这个问题在不同的设定下被反复地定义与研究，吸引了无数大神级的计算机科学家曾尝试解决这个问题，包括 Turing、Church、Buchi、Landweber、Pnueli、Clarke 等等。结论是，除了某些意义非常有限的设定，这个问题是不可判定的 [1]。换句话说，不存在这样一个万能程序。当然，更积极一点的说法是，程序员无可替代，程序员需要不停地工作来为特定的用户需求开发特定的程序，软件行业继而蓬勃发展。

 然而，毫无保留地信任程序员是要付出代价的。很快，历史证明了程序员编写的程序常常有意或者无意地包含了各种错误、安全漏洞或者后门。

计算机科学家们退而求其次，开始研究如何验证程序员编写的程序的正确性。我们的问题变成了：给定一个特定的程序和一个特定的需求（例如，没有某种特定的漏洞），我们能不能有工具可以自动的判断这个程序是不是满足需求。 这个问题同样被证明是不可判定的。我们只能依赖各种不完备的方法来尽可能找到程序的错误，或者在有限的情况下证明程序的正确性。

程序分析的方法自此百花齐放。

# 知道什么是程序正确性很难！

我们不仅放弃了保证程序正确的梦想，同时也在“正确性”的定义上节节败退。

在上个世纪，理想主义的计算机科学家们天真地认为，正确的编程方式应该是程序员先逻辑精确地表达程序的正确性需求（即 specification），然后再根据该正确性需求来实现程序，最后说明为什么该程序正确。

比如 Dijkstra 在 1969 年很自信地说过 [2]，

“After this decade, programming could be regarded as a public, mathematics-based activity of restructuring specifications into programs.” (十年之后，编程将变成一种基于数学的，把正确性需求翻译成程序的过程。）

然而并非如此。

假设“程序员会花时间把需求详细正式地写出来”已经被一而再，再而三地证明太傻太天真。刚开始的时候（也就是计算机科学家们还没有遭受现实的拷打的时候），很多 specification 语言被发明出来。比如 Oxford 的 Z 语言 [3]，Hoare 的 Communicating Sequential Processes (CSP) [4] 等等。计算机科学家们想象的是，只要我们设计的 specification 语言够直观够好用，程序员们自然就会用。毕竟，有了 specification，我们才能讨论程序正确性的问题啊。

然而并没有发生。

再后来，计算机科学家们扪心自问，为什么这么多这么好的 specification 语言都没有人用，难道是因为程序员们不愿意学一门新的语言？如果是这样，我们提供方法让程序员可以在他们常用的语言里写 specification 就好了嘛。

基于这样美好的想法，Meyer 提出了 Design-by-Contract（把程序的 specification 在程序里写成 code contract [5] [6] [7]），同时 Java Modeling Language (JML) [8] 和（基于 C# 的）SPEC# [9] 两个项目把 Meyer 的想法在主流的程序语言里几乎完美的实现了出来。

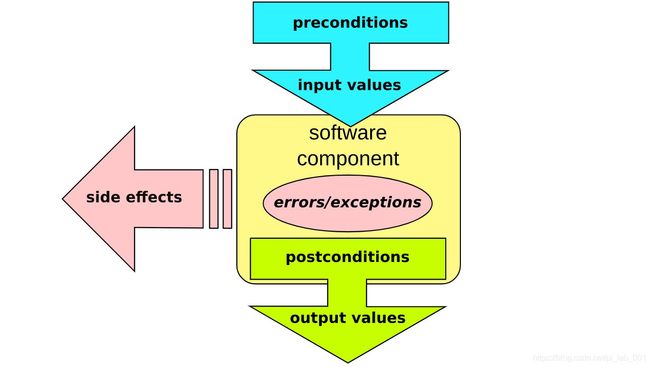A design by contract scheme

 然而并没有用。

除了少数几个项目，程序员们并不愿意花额外的时间来写 specification，即使是基于是基于 Java 或者 C#。

计算机科学家们最后的挣扎包括断言（assertion, 即“尽量在相关的地方写一些简单的检查吧”），程序标注（annotation, 即“这些标注挺有用的哈，要不相关的地方用一下啊”），测试驱动开发（test-driven development, 即“要不先写几个测试用例吧，这样我们好检查对不对”）等等。

# 程序分析技术很多! #

Was mich nicht umbringt, macht mich stärker. by Friedrich Nietzsche

“打不倒我的让我更坚强”。

从好的方面讲，因为不存在一个完美的分析程序正确性的方法，各式各样的程序分析方法层出不穷。不只是每年各种学术会议上各种 “无限完美” 的程序分析方法香火不断，致力于软件质量的行业（包括许多知名公司）也得到蓬勃发展。

通过很多年的发展，程序分析的技术和方法日趋丰富。

程序分析技术可以大致分为两类。第一类是静态程序分析，即在不执行程序的情况下进行程序分析。第二类是动态程序分析，即通过运行程序或者在程序运行期间进行分析。当然，也有很多研究工作是关于如何有效结合静态和动态程序分析的。同时，因为通常无法拿到真正的程序正确性的需求，绝大多数的程序分析技术着重于分析通用的程序正确性需求，比如如果有断言的话，我们尽量分析断言会不会被违背，再比如分析是否存在整数或者缓存溢出，再或者检测指针相关的安全漏洞等

下面，我们蜻蜓点水地介绍一下常见的两种程序分析的方法（一种理想化的和一种相对实际的），让大家大概了解它们的优缺点。

# 自动定理证明

自动定理证明（Automated Theorem Proving）[10] 是自动推理和数学逻辑的一个子领域，用于通过计算机程序证明数学定理。

其主要思想是，用某种数学逻辑来表达程序语义，同时通过基于该数学逻辑的定理推导来证明（或者证伪）程序的正确性。自动定理证明就是从 Dijkstra 那里一脉相承的理想主义的做法。常见的被用于自动定理证明的逻辑包括: propositional logic, predicate logic, first-order logic,separation logic 等等。

和传统的（人工）定理证明相比，自动定理证明可以利用各种 proof assistant（比如 Coq [11] 或者 Isabelle [12] 等）来自动检查其证明的正确性。在有限的情况下，也可以针对某些程序实现全自动的正确性证明。

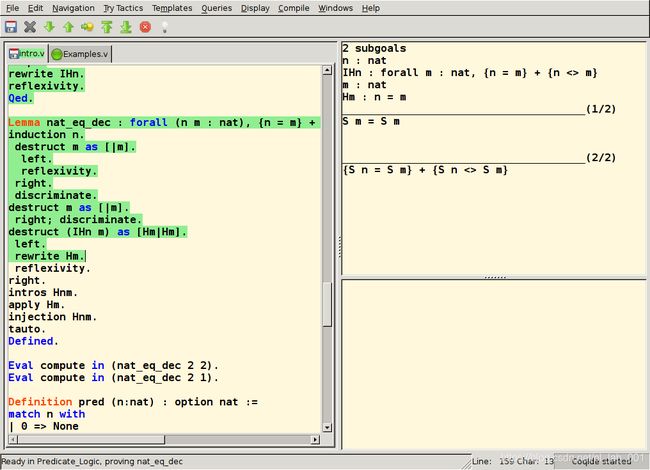CoqIDE 中的交互式证明会话，左侧为证明脚本，右侧为证明状态

## 如何用逻辑表达

在自动定理证明的方法里，程序的正确性会被表达为对应逻辑的定理。举例来说，若我们想要证明下面程序的正确性，那么我们先要确定用什么逻辑来表达该程序正确性的要求。

float sumUp (float[] array, int length) {
  float result = 0.0;
  int i = 0 ;
  while (i < length) {
    result += array[i];
    i++;
  }
  return result;
}

假设我们希望证明的是：给定任意一个 float 的数组，函数 sumUp() 都会返回该数组里所有数的和。该要求虽然比较直观，但实际上有很多细节需要考虑。

比如，如果该程序运行起来不会终止（比如有无限循环），算不算正确的？如果不算，我们就需要证明该程序（在给定一个有限长的数组的情况下）永远会终止并且终止时保证返回值是该数组里所有数的和。

再比如说，我们知道浮点数相加和数学上的整数相加并不等价，那么我们就要回答我们证明的时候用的是实数语义还是浮点数语义。理论上我们当然希望用的是浮点数语义，但是因为浮点数语义本身的复杂性，基于浮点数语义的自动定理证明通常会很难，比如证明过程太慢或者干脆证明不出来。

## 举个栗子

为了简化说明，假设我们不关心该程序是不是永远会终止的问题，同时假设我们基于实数语义来证明。那么，我们可以把该程序的正确性要求用下面的形式（叫做 Hoare Logic [13]）来表达。

// precondition:
// {array != null && length>= 0 && array.length == length}

float sumUp (float[] array, int length) { ... }

// postcondition:
// {result == sum(array[j] for all j in 0..length)}

该程序正确性有两部分组成：

• precondition 用以说明程序运行前我们假设满足的条件 比如，在上面的例子里我们假设 array 不会是 null, length 为非负数，同时 array.length 和 length 等值。
• postcondition 用以说明程序运行终止时必须满足的条件 在该例子里我们用了一个辅助函数 sum() 来（非正式地）表达我们的要求。即，函数 sumUp() 的返回值 result 必须和 array 里所有数的和等值。

在这个例子里，我们用到的是 propositional logic（包含关于实数以及预定义函数的 proposition）。如果我们需要更复杂的正确性要求，那么我们可以考虑用更复杂的逻辑来表达。

比如，如果我们想要假设不存在另外一个程序可以不通过 array 来访问该数组（即不存在 array 的 aliasing，不然我们没法保证 array 不会在 sumUp 运行时被修改），那么我们可以用例如 Separation Logic [14] 来表达我们的要求。

自动定理证明工作的原理简单来说就是，通过一些已知正确的定理来不停的推导新的结论，直到推导出我们想要的结果。就上面的例子而言，Hoare Logic 对常见的程序语句提供了多个定理来帮助我们做推导。比如下面这个可以用来推导关于 if-then-else 的程序。

 上面的定理可做如下解读：

• 如果一个 if-then-else 里的 then 分支（即 S）在同时满足 P 和 if 的判断条件 B 的情况下，运行结束时满足 Q，
• 同时，该 if-then-else 里的 else 分支（即 T）在满足 P 并且不满足 if 的判断条件 B 的情况下，运行结束时满足 Q，
• 那么我们可以推出，该 if-then-else 语句在满足 P 的情况下运行结束时满足 Q。

Hoare Logic 对每一种语句都提供了类似的定理。理论上，给定一个特定的程序，自动定理证明只需要根据不同的程序语句来运用相应的定理来不停地推导出新的结论即可。而实际上并没有那么容易，比如有些定理运用起来并没有那么容易，比如循环相关的定理需要 “无中生有” 循环不变量。

## 小结

定理证明的优势在于，我们可以在理论上证明复杂的（相对于其他方法而言）程序的正确性。当然，复杂的程序正确性的要求通常需要复杂的逻辑。

而定理证明的缺点是，现有的自动定理证明工具的自动化程序并没有我们想要的高。我们常常需要给自动定理证明工具提供额外的帮助，比如提供循环不变量，或者提供详细的如何一步一步来运用各种定理的步骤。

基于此原因，定理证明可以说并不适合作为一个常规的程序分析方法，除非允许投入相当大的成本。相对而言，定理证明比较适合用来证明某些特定的库（比如加密算法）或者核心代码（比如内核安全 policy）的实现的正确性。

# 抽象解释

抽象解释（Abstract Interpretation）是一种简化程序语义从而更高效的进行程序分析的方法。

其核心思想是，如果我们对程序正确性的要求比较简单, 那么我们很可能不需要分析所有的程序语义来证明该程序的正确性。比如，我们如果只关心数组索引会不会越界，那么我们只需要分析作为数组索引的变量的可能取值范围就够了。

在运用抽象解释方法的时候，我们先要确定什么抽象域适合我们的程序正确性要求。

## 如何选择适合的抽象域

在抽象解释方法里，程序的正确性通常表达为一个确定的抽象域里的断言（assertion）。常见的抽象域包括：

• 污点（taint），仅关心变量是否受污染
• 区间（interval），仅关心变量的取值区间
• difference-bound matrix，仅关心任意两个变量之前的差值

等等。以下面的程序为例，

//precondition: y is an array with 10001 elements
void f() {
1.  int x = 1;
2.  while (x < 10000) {
3.    x = x+1;
    }
4.  y[x] = 1;
}

假设我们只是想证明该程序的第 4 行 y[x] = 1 不会有 indexoutofboundexception，那么我们关心的仅仅是 x 的取值范围会不会超过某个安全的范围。因此，我们可以选择区间作为我们的抽象域来进行抽象解释，我们的正确性要求就可以写成下面的断言：

assert(x>= 0 && x<= 10000)

要注意的是，在该抽象域里，我们只允许写关于单个变量的取值范围的断言，而不能写更复杂的，比如两个变量的和必须小于某个数这种）。更复杂的正确性要求通常需要更复杂的抽象域。同时，一个正确性要求能在某个抽象域写出来，不代表能在该抽象域通过抽象解释的方法证明或者证伪（就是说，简单的断言也可能需要更复杂的抽象域才能证明）。

简单来说，抽象解释的方法可以用以下简单的算法来概括：

• 第一步，选择一个抽象域
• 第二步，根据选择的抽象域抽象所有的变量初值
• 第三步，根据选择的抽象域抽象每一个程序语句
• 第四步，运行抽象完的程序来判断断言是不是满足

## 举个栗子

我们用上面的程序例子来说明抽象解释的这几个步骤。鉴于我们仅关心 x 的取值范围，为了简化讨论，我们在下面忽略掉 y，并且我们假设 x 是数学上的整数。

我们可以将抽象解释理解为通过抽象每一句语句生成如下的 “抽象” 的程序：

A.  x_interval_1 = [1, 1];
B.  while (*) {
C.    x_interval_2 = (x_interval_1 ∪ x_interval_3) ∩ ([-∞, 9999])
D.    x_interval_3 = x_interval_2 + [1, 1]
    }
E.  x_interval_4 = (x_interval_1 ∪ x_interval_3) ∩ ([10000, +∞])

前面的程序例子中，每一个程序语句都被抽象成了一个对应的的抽象语句，同时其整个程序的结构保持不变，其中每一个语句抽象的时候要保证其语义在指定的抽象域上不会丢失行为（允许增加行为）。

原程序中的第一行 int x = 1 被 A 抽象，即 x_interval_1 = [1, 1]。其中变量 x_interval_1 代表的是 x 在第一行运行完后的区间。

原程序里第二行的循环 while (x < 10000) 被上面的 C 和 E 抽象。其中 C 的直观的解读是，x 在第二行结束后的区间为 x 在第一行运行完后的区间与 x 在第三行运行完后的区间的合集（因为第二行可能从第一行或者第三行到达），再并上循环条件要求的区间 [-∞, 9999]。

其他的抽象同理可得。注意上面的例子里所有的操作（包括 ∪，∩，和 +）都是定义在区间上的操作。

得到这个抽象版本的程序以后，我们运行这个抽象程序以得到 x_internval_4 的值，从而来判断是不是可以推出上面的断言永远满足。

## 小结

抽象解释因为其高效简洁的特点，可以广泛地用来分析各种程序。一个常见的应用是，通过抽象解释来快速分析安全相关的程序，以检查其是否存在各种安全漏洞（比如常见的整数溢出，缓存溢出，指针的 use-after-free，线程死锁等）。经过几十年的发展，针对不同的程序与不同的正确性要求，工业界已经发展出很多抽象解释的工具了，比如 Coverity [15] 和 Sparrow [16] 等。

基于抽象解释的工具常被人诟病的是，这些工具经常会有很高的误报率（假警报）。误报的根本原因在于，抽象解释通过抽象每一句程序语句来减少程序分析的复杂度，因此会不可避免地丢失了很多程序里的信息，从而不能准确判断程序的行为。此外，因为抽象解释设计的原则是不能有漏报（即不能丢失，只能增加程序的行为），这样就不可避免地会增加误报的现象。

可以减少抽象解释误报的方法包括选择更精确的抽象域（以增加分析成本为代价），或者结合其他的程序分析技术，比如通过模糊测试来过滤可能的误报。

# 其他常见的方法

以上只是粗略的介绍了两种程序分析的方法。其他常见的方法还包括，符号执行（通过用求解每条程序路上上的条件来生成测试用例），模型检测（通过抽象并遍历所有的程序行为来判断程序是不是正确），模糊测试（通过优化大量的生成测试用例）等等。

# 当前程序分析研究领域浅析 #

当前程序分析的研究大致可以分为两个部分：一是关于程序分析技术本身，二是把程序分析技术运用到新的领域。

就程序分析技术本身而言，很多值得研究的问题不断有新的进展。

比如提供更好的语言和工具让程序员更容易的描述程序的正确性。这个方向最新的一个尝试可能是现在差不多算夭折了的 Move 语言 [17]（一个针对智慧合约的编程语言）。在 Move 的设计里，程序员需要通过 precondiction 和 postcondition 来描述程序的正确性要求。当然这个愿望很美好，具体效果我们可能永远没法知道了。

再比如，对基于静态分析（比如抽象解释，或者 lint）的工具，一个重要的问题就是如何减少假警报的。而对于动态分析（比如测试）而言，对应的问题就是如何减少漏报。

除了把静态分析做的更精确（比如设计更复杂的 lint 规则），和把动态分析做的更完备（比如提要求更高的覆盖率标准），还有一个趋势，就是结合不同的程序分析技术取长补短。比如 hybrid fuzzing 的做法是，通过有效的结合符号执行与模糊测试来提高测试的覆盖率。

此外，程序分析技术和工具也越来越多的被用来辅助解决别的问题。比如近来热门的程序修复技术大多是基于不同的程序分析技术。

程序分析技术也越来越被用来分析一些非传统的 “程序” 上，比如智慧合约和神经网络。

智慧合约，简单的理解就是基于区块链运行的，相对简单的程序。传统程序有的问题（比如各种安全漏洞）智慧合约基本都有。同时，智慧合约的正确性要求和设计又和传统程序有所不同，这样就需要我们针对智慧合约适配现有的程序分析。近期有很多把静态分析和动态分析技术移植到智慧合约的工作。

神经网络可以看作是一类不是基于逻辑的程序，甚至从某些层面上说，神经网络有点接近我们文章开头提到的理想中的万能程序。当然，和传统程序一样，神经网络也有各种各样的正确性问题（比如鲁棒性，没有后门，公平性等等）。至少理论上，我们可以适配现有的程序分析技术来分析神经网络。这块已经有不少工作了，比如 ETH 有一系列把抽象解释用到神经网络上的工作。当然，因为神经网络和传统程序的很大不同，很多程序分析的技术不再适用（比如因为不存在 “程序” 路径，针对神经网络的符号执行也无从谈起）。未来这块应该会有很多工作可以期待一下。

# 总结 #

总的来说，程序分析有各种不同的方法。各种方法有不同的适用场景而且需要的代价也不同。这就需要大家理智的选择合适的程序分析的方法。总的原则可以是，有总比没有好，如果太贵就算了。

---

---

 参考

[1] Undecidable Problem - Wikipedia https://en.wikipedia.org/wiki/Undecidable_problem

[2] O. J. Dahl, E. W. Dijkstra, and C. A. R. Hoare, editors. Structured Programming. Academic Press Ltd., GBR, 1972. https://dl.acm.org/doi/book/10.5555/1243380

[3] Jean-Raymond Abrial, Stephen A. Schuman, and Bertrand Meyer. A Specification language. In R. M. McKeag and A. M. Macnaghten, editors, On the Construction of Programs, pages 343–410. Cambridge University Press, 1980.

[4] C. A. R. Hoare. Communicating sequential processes. Commun. ACM, 21(8):666–677, August 1978. https://doi.org/10.1145/359576.359585

[5] Design by Contract, Technical Report TR-EI-12/CO, Interactive Software Engineering Inc., 1986.

[6] Design by Contract, in Advances in Object-Oriented Software Engineering, eds. D. Mandrioli and B. Meyer, Prentice Hall, 1991, pp. 1-50.

[7] Applying "Design by Contract", in Computer (IEEE), 25, 10, October 1992, pages 40-51.

[8] Gary T. Leavens, Albert L. Baker, and Clyde Ruby. JML: A Notation for Detailed Design, pages 175–188. Springer US, Boston, MA, 1999. https://link.springer.com/chapter/10.1007/978-1-4615-5229-1_12

[9] Mike Barnett, K. Rustan M. Leino, and Wolfram Schulte. The spec# program-ming system: An overview. In Gilles Barthe, Lilian Burdy, Marieke Huisman,Jean-Louis Lanet, and Traian Muntean, editors, Construction and Analysis ofSafe, Secure, and Interoperable Smart Devices, pages 49–69, Berlin, Heidelberg, 2005. Springer Berlin Heidelberg. https://link.springer.com/chapter/10.1007/978-3-540-30569-9_3

[10] Authomated Theorem Proving - Wikipedia https://en.wikipedia.org/wiki/Automated_theorem_proving

[11] The Coq Proof Assistant. https://coq.inria.fr/

[12] Isebelle: A generic proof assistant. https://isabelle.in.tum.de

[13] C. A. R. Hoare. An axiomatic basis for computer programming. Commun. ACM, 12(10):576–580, October 1969. https://dl.acm.org/doi/10.1145/363235.363259

[14] J.C. Reynolds. Separation logic: a logic for shared mutable data http://structures.In Proceedings 17th Annual IEEE Symposium on Logic in Computer Science, pages 55–74, 2002. https://ieeexplore.ieee.org/document/1029817

[15] Coverity Static Application Security Testing https://www.synopsys.com/software-integrity/security-testing/static-analysis-sast.html

[16] The Sparrow Static Analyzer. http://ropas.snu.ac.kr/sparrow/

[17] The Move Programming Language https://move-book.com/