学习笔记——吴恩达《神经网络与深度学习》
神经网络与深度学习
- 1. 基础知识
-
-
- 神经网络
- 用神经网络进行监督学习
-
- 2. 神经网络基础知识
-
-
- 二分分类
- logistic回归
- logistic回归损失函数
- 梯度下降法
- 导数
- 计算图
- logistic回归中的梯度下降法
- m个样本的梯度下降
- 向量化
- Python中的广播
-
- 3. 浅层神经网络
-
-
- 神经网络概述
- 神经网络表示
- 计算神经网络的输出
- 多个样本的向量化
- 激活函数
- 激活函数的倒数
- 神经网络的梯度下降法
- 随机初始化
-
- 4. 深层神经网络
-
-
- 深层神经网络概述
- 深层网络中的前向传播
- 核对矩阵的维数
- 为什么使用深层表示
- 搭建深层神经网络块
- 前向和反向传播
- 参数 VS 超参数
-
1. 基础知识
神经网络
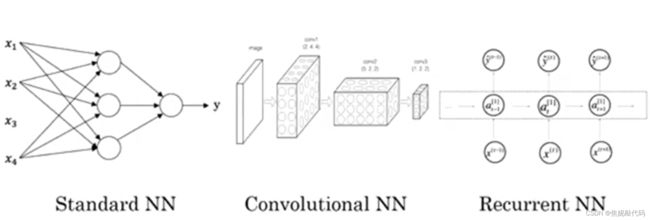
深度学习指的是训练神经网络,神经网络的一部分神奇之处在于:当你实现他之后,你要做的只是输入x,就能得到输出y(不管训练集有多大),所有的中间过程 它都会自己完成。
这有四个输入的神经网络,输入的特征可能是卧室的数量、邮政编码 和周边的富裕程度,已知这些输入的特征,神经网络的工作就是预测对应的价格。
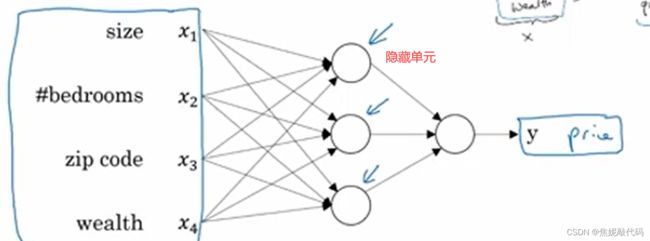
对于神经网络,只有你喂给它足够多的数据(关于x和y的数据),给到足够的x、y训练样本,神经网络非常擅长于计算从x到y的 精准映射函数。
用神经网络进行监督学习
在监督学习中,输入x,习得一个函数映射到输出y。比如我们之前看到的应用于房价预测的例子,输入房屋的一些特征,就能输出或者预测价格y。
结构化数据是数据的数据库,例如在房价预测中,你可能有一个数据库或者数据列,告诉你房间的大小和卧室数量,这就是结构化数据。结构化数据意味着每个特征,比如说房屋大小 卧房数量都有着清晰的定义。
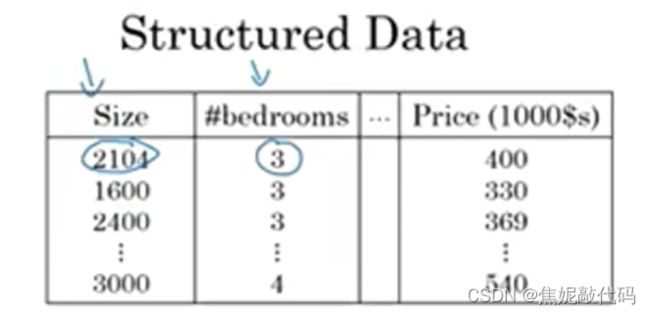
相反,非结构化数据指的是比如音频、原始音频、图像。这里的特征可能是图像中的像素值,或者是文本中的单个单词。
2. 神经网络基础知识
二分分类
神经网络的计算过程中,通常有一个正向过程(正向传播步骤),接着会有一个反向步骤(反向传播步骤)。
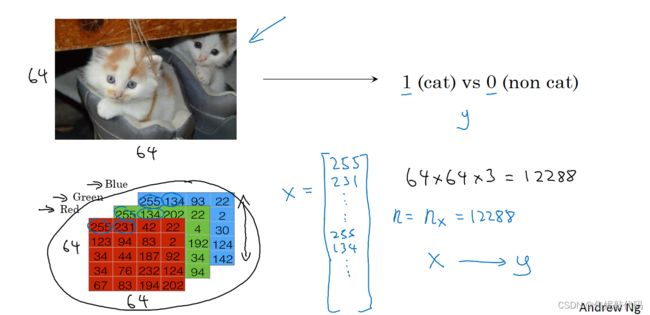
logistic回归是一个用于二分分类的算法,这有一个二分分类问题的例子:假如你有一张图片作为输入,你想输出识别此图的标签,如果是猫输出1,如果不是则输出0,我们用y来表示输出的结果标签。
来看看一张图片在计算机中是如何表示的,计算机保存一张图片要保存三个独立矩阵,分别对应图片中的红、绿、蓝三个颜色通道。如果输入图片是64×64像素的,就有三个64×64的矩阵分别对应图片中 红、绿、蓝三种像素的亮度。
为了把这些像素值取出放入特征向量,就要像下面这样定义一个特征向量x以表示这张图片,我们把所有的像素值都取出来 例如255、231这些,最后得到一个很长的特征向量。如果图片是64×64的,那么向量x的总维度就是64×64×3。我们用nx=12288来表示输入的特征向量x的维度。
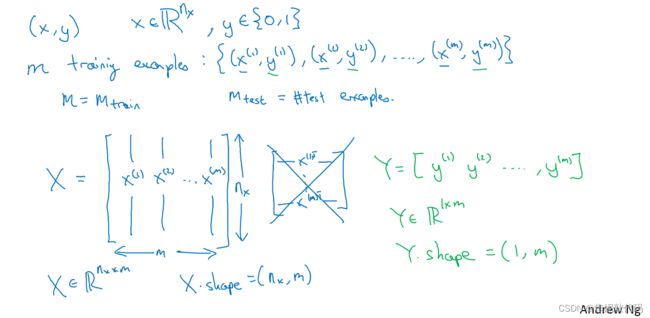
在二分分类问题中,目标是训练出一个分类器。它以图片的特征向量x作为输入,预测输出的结果标签y是1还是0。用一对(x,y) 来表示一个单独的样本,x是nx维的特征向量,标签y 值为0或1。训练集由m个训练样本构成,(x(1) ,y(1))表示样本一的输入和输出。
用更紧凑的符号表示训练集,我们定义一个矩阵 用大写的X表示,它由训练集中的x1、x2这些组成,把x(1)放进矩阵的第一列,x(2)是第二列 …… xm是第m列,最后得到矩阵X。这个矩阵有m列,这个矩阵的高度记为nx。
logistic回归
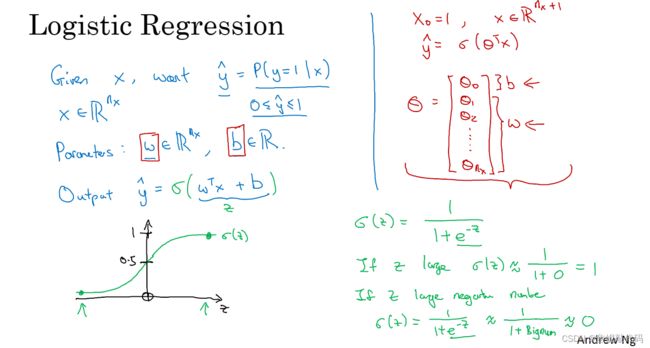
已知的输入特征向量x,你希望把识别出这是不是猫图,你需要一个算法可以给出一个预测值,我们说预测值y帽就是你对y的预测。你希望y帽是一个概率,当输入特征x满足条件时y就是1。
已知Logistic回归的参数是w(也是一个nx维向量),而b就是一个实数。所以已知输入x和参数w和b,y帽可以定义为y帽 = wT x +b,即输入x的线性函数。但这不是一个非常好的二元分类算法,因为你希望y帽是y=1的概率,所以y帽应该介于0和1之间,但实际上这很难实现 因为wTx+b,可能比1大得多或者甚至是负值,这样的概率是没意义的。
所以在Logisitc回归中 我们的输出变成:y帽等于sigmoid函数作用到这个量上,sigmoid(z)就是这样的从0到1的光滑函数。所以当你实现logistic回归时,你要做的是学习参数w和b,所以y帽变成了比较好的估计。
logistic回归损失函数
为了训练logistic回归模型的参数w以及b,需要定义一个成本函数,用logistic回归来训练的成本函数。为了让模型来通过学习调整参数,要给一个m个样本的训练集。你想通过在训练集找到参数w和b来得到你的输出。
我们通过定义损失函数L,来衡量你的预测输出值y帽 和y的实际值有多接近。误差平方看起来似乎是一个合理的选择,但用这个的话梯度下降法就不太好用。在logistic回归中 ,我们使用如下一个误差函数,我们也想让他尽可能的小。
- 当y=1时,就是-log(y帽) 。你想让-log(y帽)尽可能小,这意味着想让log(y帽)够大尽可能地大,这样就意味你想要y帽够大,但是因为y帽是simoid函数得出的(永远不会比1大),所以你要让y帽接近1。
- 当y=0时,就只有损失函数的第二项,想让损失函数小一些,也就意味着你想要log(1-y帽)够大,即y帽尽可能地小接近0。
损失函数是在单个训练样本中定义的,它衡量了在单个训练样本上的表现。
成本函数它衡量的是在全体训练样本上的表现。成本函数为1/m分之所有训练样本的损失函数和
梯度下降法
损失函数是衡量单一训练样例的效果,成本函数用于衡量参数w和b的效果(在全部训练集上来衡量)。我们要得到使得成本函数J(w, b)尽可能小的w和b。
为了找到更好的参数值,我们要做的就是用某初始值初始化w和b,通常用0来进行初始化。
梯度下降法所做的就是从初始点开始,朝最陡的下坡方向走一步。
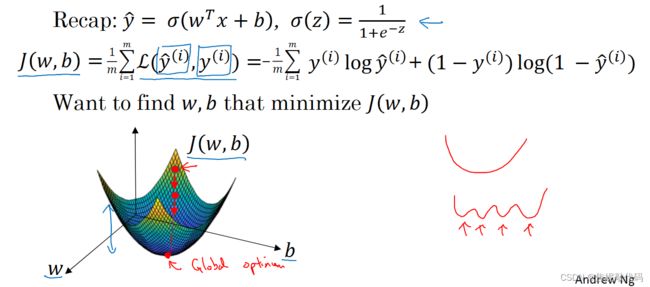
为了方便,先忽略b,仅仅是用一维曲线来代替多维曲线,梯度下降法是这样做的,我们将重复执行以下的更新操作:让w=w-αdJ(w)/dw,直到算法收敛。α表示学习率,学习率可以控制每一次迭代或者梯度下降法中的步长,dJ(w)/dw这就是对参数w的更新或者变化量,导数的定义是函数在这个点的斜率。
在logistic回归中 你的成本函数,是一个含有w和b的函数,你必须通过w:=w-α dJ(w,b)/dw 更新w,通过b:=b-α dJ(w,b)/db 更新b。
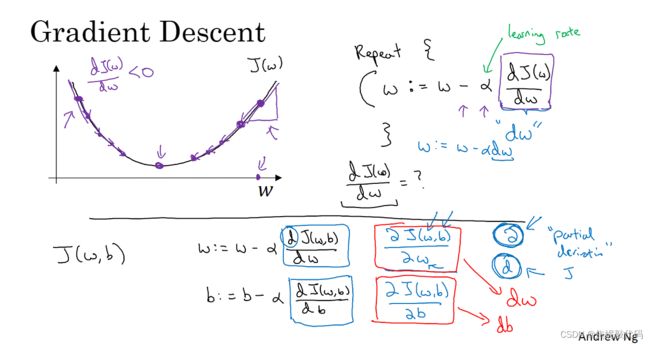
导数
计算图
一个神经网络的计算都是按照前向或反向传播过程来实现的,首先计算出神经网络的输出,紧接着进行一个反向传输操作。
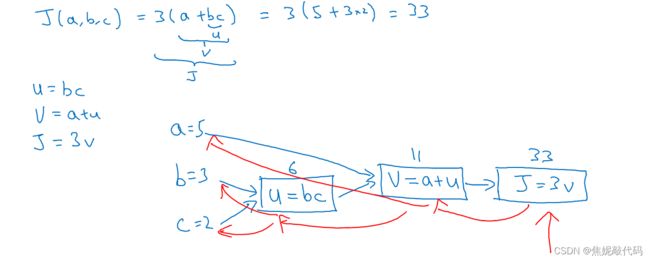
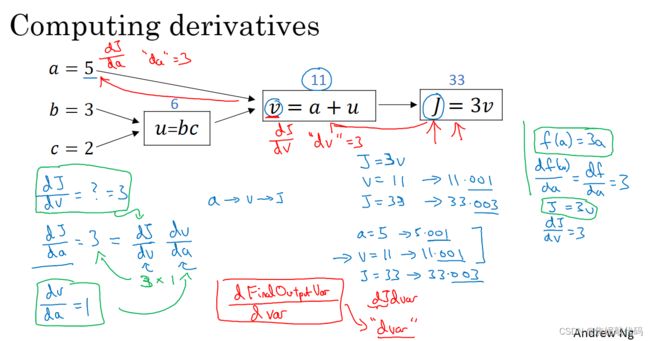

在反向传播算法中的术语 我们看到如果你想计算最后输出的变量的导数,使用你最关心的变量对v的导数,那么我们就做完了一步反向传播
logistic回归中的梯度下降法
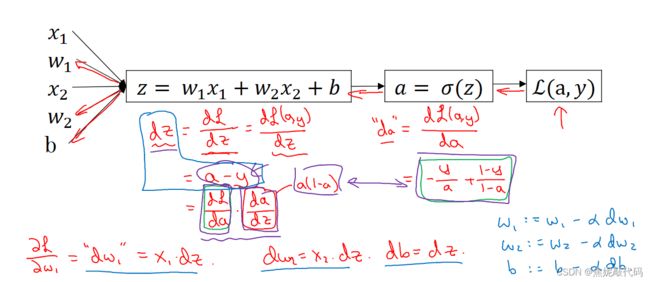
假设样本只有两个特征x1和x2。为了计算z,我们需要输入参数w1、w2和b,还有样本特征值x1 x2,得z等于w1x1+w2x2+b。然后计算y帽 (sigma(z) )、最后计算L(a,y)。
因此在logistic回归中,我们需要做的是变换参数w和b的值,来最小化损失函数。在前面,我们已经前向传播步骤,在单个训练样本上计算损失函数。
关于单个样本的梯度下降法,使用这个公式计算dz,使用这个计算dw1、dw2、还有db 然后更新w1为 w1减去学习率乘以dw1,类似地更新w2、b。
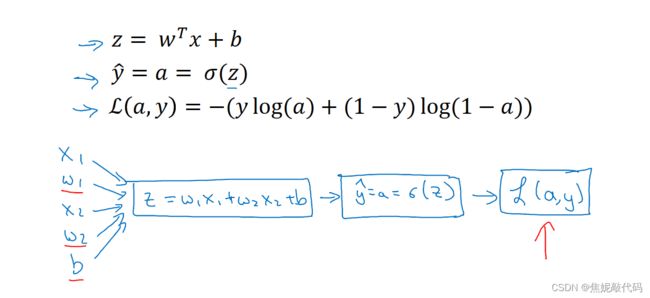
m个样本的梯度下降
成本函数J(w,b)的定义,它是这样一个平均值:1/m 从i=i到m求和这个损失函数。
即全局成本函数对w1的导数,也同样是各项损失函数对w1导数的平均。所以你真正需要做的是计算这些导数并且求平均,这会得到全局梯度值(能够把它直接应用到梯度下降算法中)

让我们初始化J=0,dw1等于0 dw2等于0 db等于0。并且我们将要做的是使用一个for循环遍历训练集,同时计算相应的每个训练样本的导数,然后把它们加起来。 如我们所做的让i 等于1到m(m正好是训练样本个数),并计算如下式子。

向量化
我们可以用内置函数 避免使用显示for循环,比如np.dot
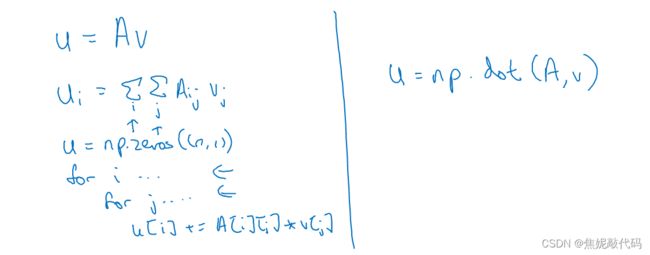
每当你想写一个for循环时,应该看看可不可以调用numpy用内置函数计算 而不是用for循环

这里有个Python巧妙的地方,在这个地方b是一个实数或者你可以说是1×1的矩阵,但是当你把向量加上这个实数时,Python会自动的把实数b扩展成一个1×m的行向量,在Python中这叫做广播
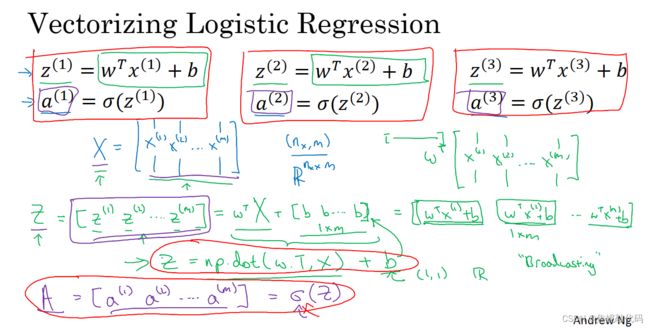


Python中的广播
a=np.random.randn(5,1)
代替
# 秩为1的数组,它的行为和行向量或列向量并不一样
a=np.random.randn(5)
3. 浅层神经网络
神经网络概述
首先,我们用x表示输入特征,还有参数W和b。x上标(i)表示第i个训练样本,上标方括号1 2表示不同的层 这是网络的第一层 这是第二层。
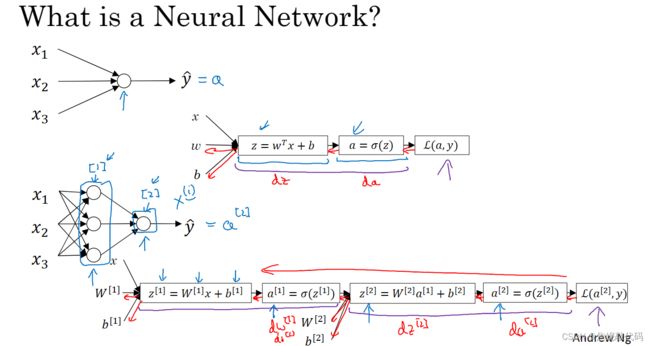
神经网络表示
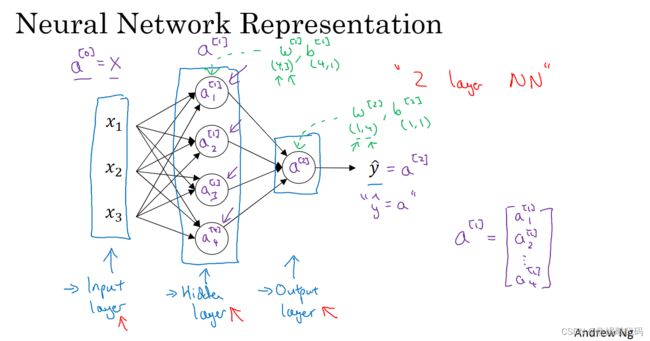
这是一张神经网络图,我们命名一下这张图的各部分:
- 我们有输入特征x1 x2 x3 竖向堆叠起来,这是神经网络的
输入层。它包含了神经网络的输入 - 另外一层的圆圈,我们称之为神经网络的
隐藏层 - 这个只带一个节点的层就是
输出层,它负责输出,并预测值y帽
在一个神经网络中 当你使用监督学习训练它的时候,训练集包含了输入x,还有目标输出y。“隐藏层”的含义是在训练集中这些中间节点的真正数值我们是不知道的,在训练集你看不到它们的数值,你能看到输入值也能看见输出值,但是隐藏层中的值在训练集中是无法看到的。输入层将x的值传递给隐藏层。
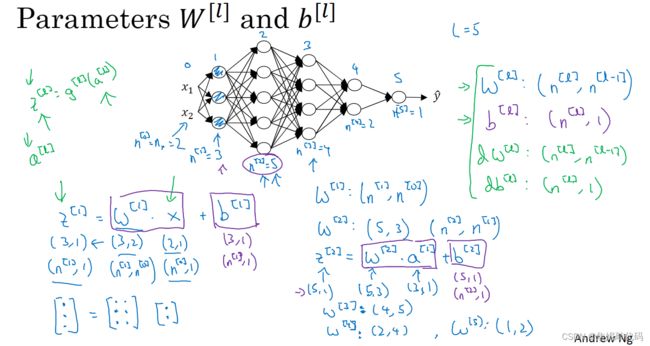
隐藏层以及最后的输出层是带有参数的,这里的隐藏层有两个相关的参数W和b。第一层的W是一个4x3的矩阵,而b在这个例子中是一个4x1向量,第一个数字4意思是有四个节点 或者说四个隐藏单元,然后数字3来自这里有三个输入特征。
计算神经网络的输出
Logistic回归这里的圆圈代表了回归计算的两个步骤,首先你按步骤计算出z,然后在第二步计算激活函数就是函数sigmoid(z),所以神经网络只不过重复计算这些步骤很多次。
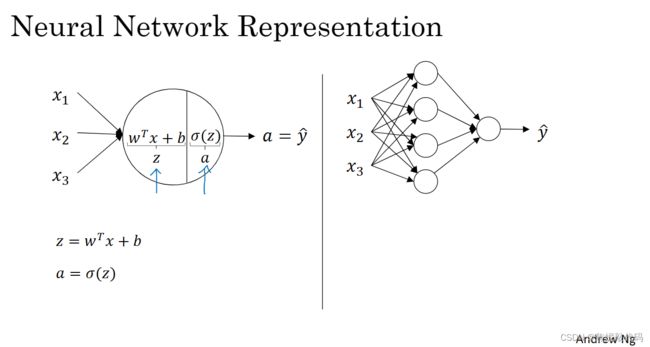
看看这个隐层的第一个节点(暂时先隐去其他的节点),左边看上去和Logistic回归很相似。
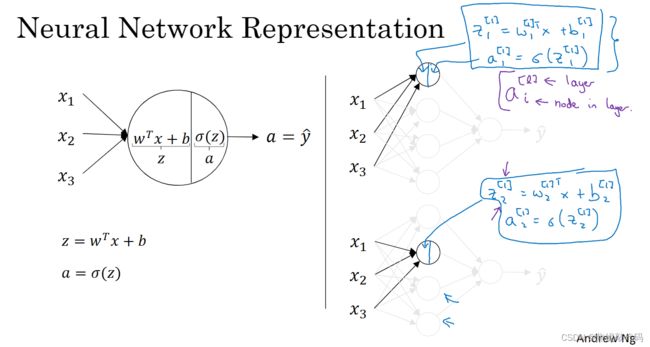
向量化时,当我们在一层中有不同的节点,那就纵向堆叠起来
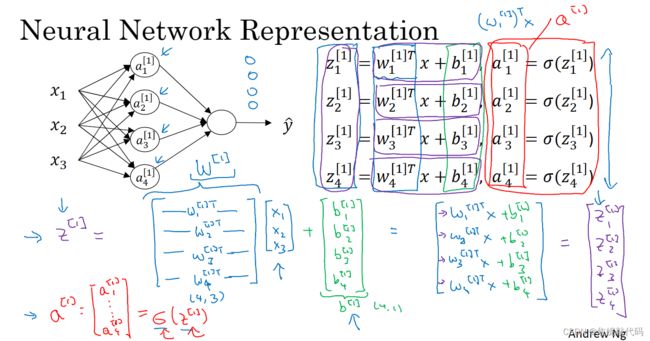
归纳一下:对于Logistic回归,为了计算输出或者说预测,你要计算z = w^T x + b和 y帽 = a = sigmoid(z),当你有一个单隐层神经网络,你需要去在代码中实现的是计算这四个等式

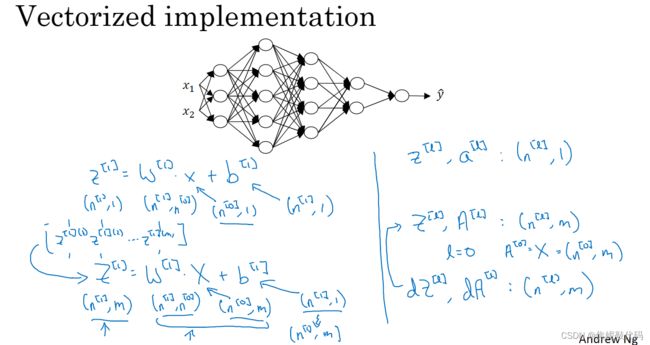
多个样本的向量化
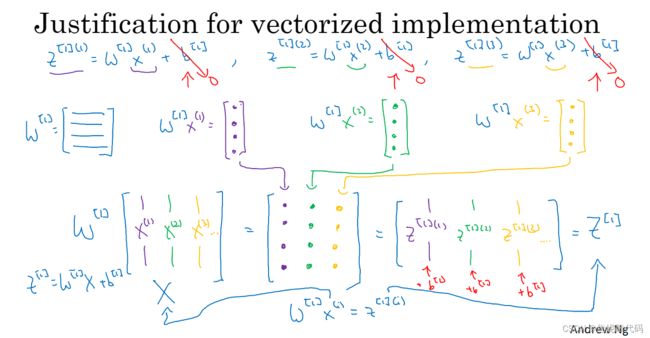
比如矩阵A和Z,横向的话我们有对所有训练样本用指标排序,所以横向指标就对应了不同的训练样本,当你从左到右扫的时候就扫过了整个训练集。而在竖向,竖向指标就对应了神经网络里的不同节点,对应隐藏单元。


激活函数
- σ函数介于0和1之间。
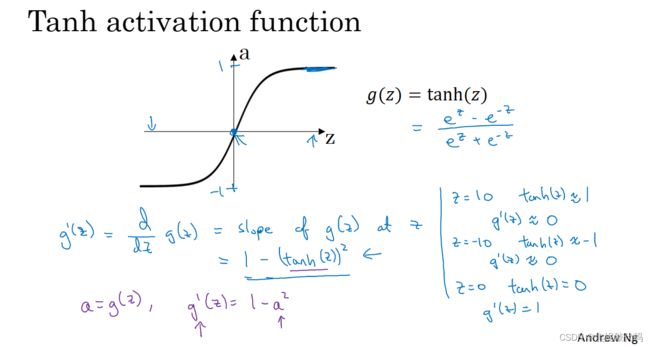
- tanh函数或者叫双曲正切函数,这函数介于-1和1之间,使用tanh而不是σ函数也有类似数据中心化的效果,使得数据的平均值接近0。
现在σ函数和tanh函数都有的一个缺点就是:如果z非常大或非常小,那么导数的梯 或者说这个函数的斜率可能就很小(接近0),这样会拖慢梯度下降算法。所以出现了比较受欢迎的修正线性单元(ReLU)。
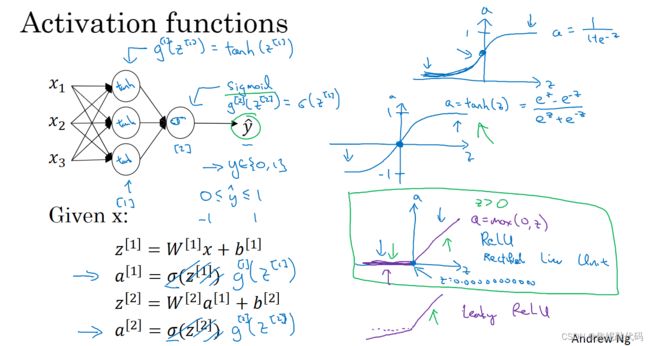
在选择激活函数时有一些经验法则
- 如果你的输出值是0和1,如果你在做二元分类,那么σ函数很适合作为输出层的激活函数。
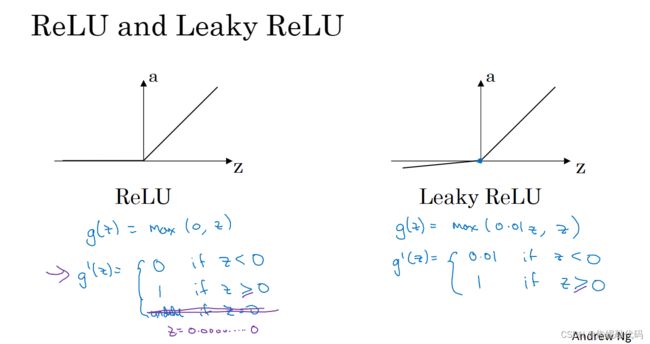
- 然后其他所有单元都用ReLU。而ReLU的一个缺点是,当z为负时导数等于零。但ReLU还有另一个版本叫做带泄漏的ReLU(当z为负时 函数不再为0),这通常比ReLU激活函数更好,不过实际中使用的频率没那么高。
ReLU和带泄漏的ReLU好处在于,对于很多z空间,激活函数的导数激活函数的斜率和0差很远,所以在实践中使用ReLU激活函数,你的神经网络的学习速度通常会快得多

如果你要用线性激活函数或者叫恒等激活函数,那么神经网络只是把输入线性组合再输出。

激活函数的倒数
当你对你的神经网络使用反向传播的时候,你真的需要计算激活函数的斜率或者导数。在微积分中g’(z) 上面这一撇叫prime,在微积分中表示函数g对输入变量z的导数
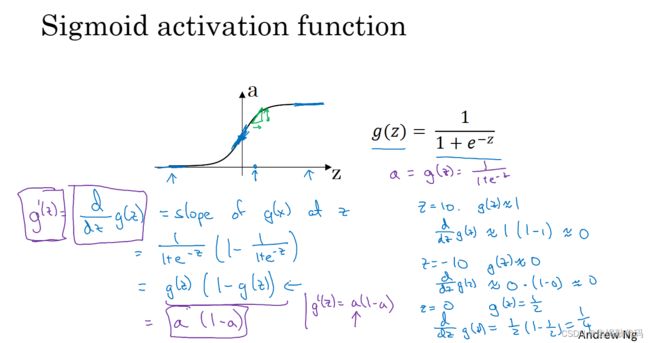
神经网络的梯度下降法
随机初始化
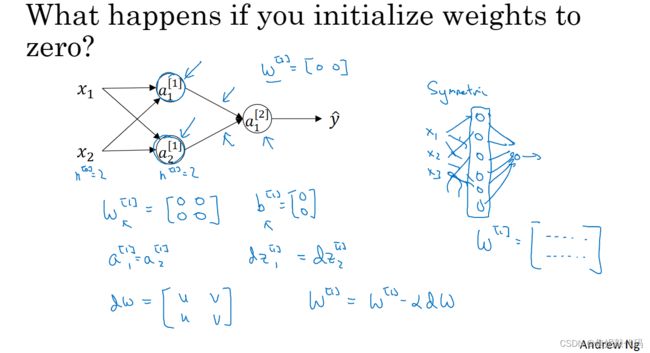
当你训练神经网络时,随机初始化权重非常重要,对于logistic回归可以将权重初始化为零。但如果将神经网络的各参数数组全部初始化为0,再使用梯度下降算法,那会完全无效。
将偏置项b初始化为0实际上是可行的,但把W初始化成全零就成问题了,这种初始化形式的问题在于,你给网络输入任何样本 你的a11和a12是一样的。
如果你将W所有值初始化为0,那么因为两个隐藏单元一开始就在做同样的计算,两个隐藏单元对输出单元的影响也一样大。那么在一次迭代之后,同样的对称性依然存在,两个隐藏单位仍然是对称的。无论你训练神经网络多长时间,两个隐藏单元仍然在计算完全一样的函数,所以在这种情况下多个隐藏单元真的没有意义。
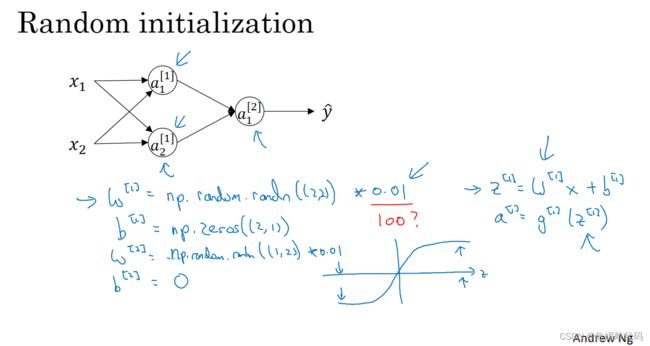
通常,我们喜欢把权重矩阵初始化成非常非常小的随机值。因为如果你用的是tanh或者sigmoid激活函数,那权重太大当你计算激活函数值时,W很大 z就会很大(或者这些z值会很大或者很小)。所以在这种情况下,你最后可能落在这些tanh函数或者sigmoid函数的平缓部分,梯度的斜率非常小,意味着梯度下降法会非常慢,所以学习会很慢。
4. 深层神经网络
深层神经网络概述
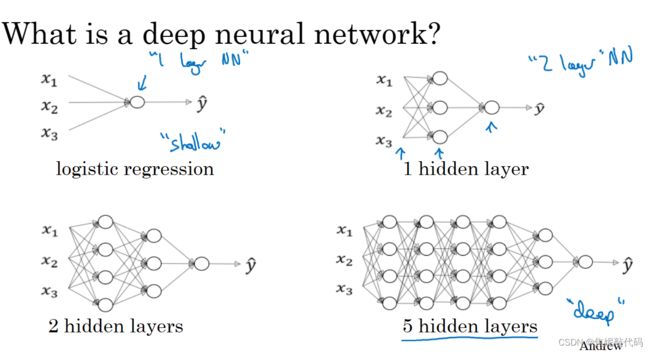
计算神经网络的层数时,我们不能把输入层数进去,只算上隐层的数量和输出层。
深层网络中的前向传播
核对矩阵的维数
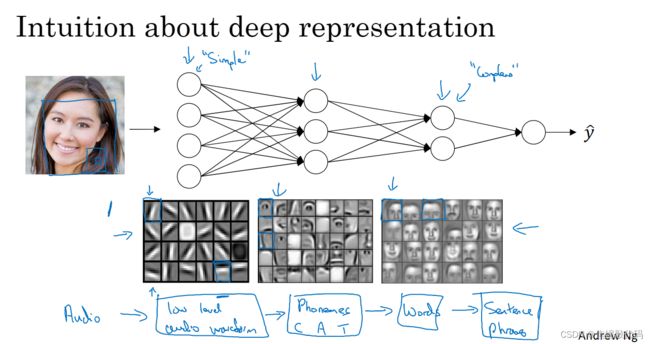
为什么使用深层表示
搭建深层神经网络块
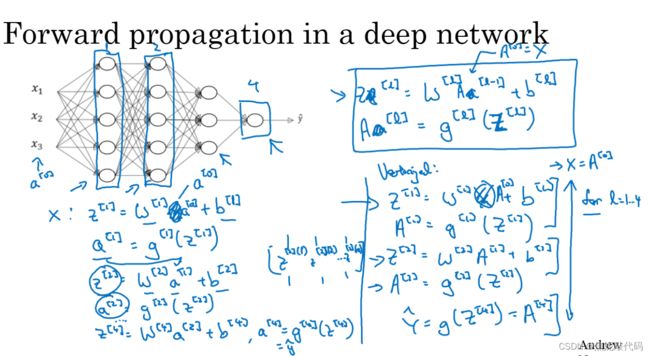
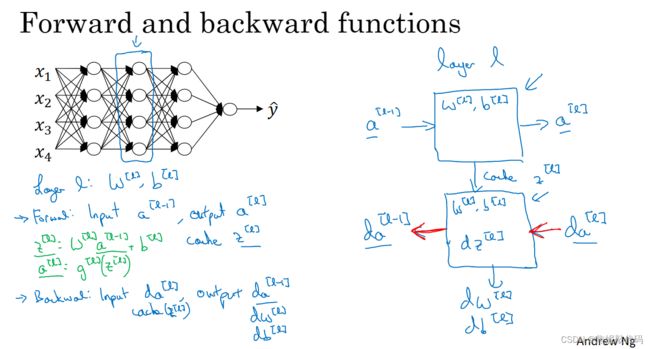
把输入特征a[0],放入第一层并计算第一层的激活函数(用a[1]来表示),你需要w[1]和b[1]来计算,之后也缓存z[1]值。之后到了第二层,需要用到w[2]和b[2],你会需要计算第二层的激活函数a[2] 。以此类推,直到最后一个,在这些过程里我们缓存了所有的z值,这就是正向传播的步骤。
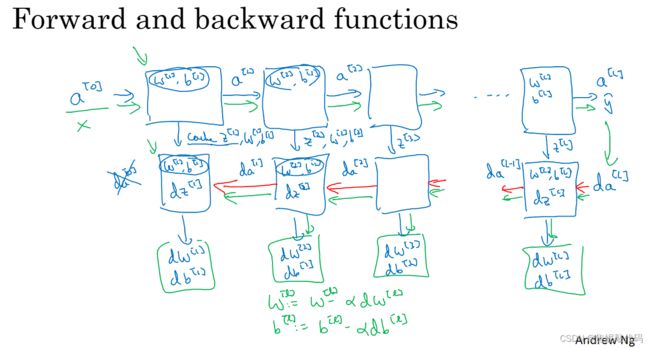
对反向传播的步骤而言,我们需要算一系列的反向迭代,就是这样反向计算梯度。现在你就有所有的导数项了,w也会在每一层被更新为W减去学习率乘以dW,b也一样。
前向和反向传播
参数 VS 超参数
我们知道模型里有参数W和b,但在学习算法中还有其他参数需要输入到学习算法中,比如学习率α、或者还有梯度下降法循环的数量。在你的算法中也许也有其他你想要设置的数字比如隐层数L,你还可以选择激活函数、用修正线性单元 还是tanh。那么算法中的这些数字都需要你来设置,这些数字实际上控制了最后参数W和b的值,所以它们被称作超参数。
因为这些超参数比如α即是学习率、循环的数量、隐层的数量等等都是能够控制W和b的所以这些东西称为超参数。因为这些超参数某种程度上,决定了最终得到的W和b。实际上深度学习有很多不同的超参数