NNDL 作业3：分别使用numpy和pytorch实现FNN例题

1. 过程推导 - 了解BP原理
2. 数值计算 - 手动计算，掌握细节
3. 代码实现 - numpy手推 + pytorch自动

过程推导、数值计算，以下三种形式可任选其一：

• 直接在博客用编辑器写
• 在电子设备手写，截图
• 在纸上写，拍照发图 

参见实验结尾部分，这里不再重复：

NNDL 实验五 前馈神经网络（1）二分类任务_真不想再学了的博客-CSDN博客

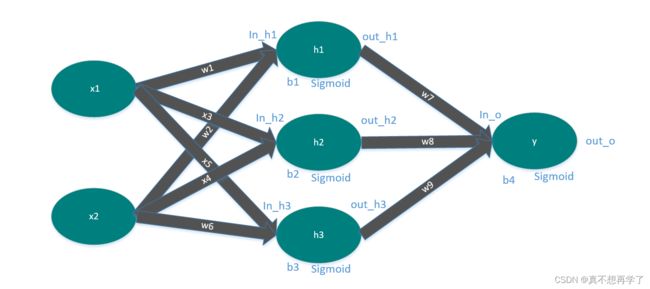
代码实现：新建了一个神经网络，且为神经元加上了偏置b

神经网络如下：

 首先numpy实现：

#coding:utf-8

import numpy as np

def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a

def forward_propagate(x1, x2):
    '''传入输入和参数'''
    '''隐藏层'''
    in_h1 = w1 * x1 + w2 * x2+b1
    out_h1 = sigmoid(in_h1)
    in_h2 = w3 * x1 + w4 * x2+b2
    out_h2 = sigmoid(in_h2)
    in_h3 = w5 * x1 + w6 * x2 + b3
    out_h3 = sigmoid(in_h3)
    '''输出层'''
    in_o =w7*out_h1+ w8 * out_h2 + w9 * out_h3+b4
    out_o = sigmoid(in_o)
    '''输出隐藏层输出和输出层输出'''
    return out_o, out_h1, out_h2,out_h3


def back_propagate(out_o,out_h1, out_h2,out_h3):
    '''传入隐藏层出和输出层输出'''
    # 反向传播
    '''计算均方误差的第一层偏导'''
    '''(y-y')'''
    d_o= out_o - y
    '''计算误差对参数w7、w8、w9的偏导数'''
    '''d_w7=(y-y')*y*(1-y)*h_1'''
    d_w7 = d_o * out_o * (1 - out_o) * out_h1
    d_w8 = d_o * out_o * (1 - out_o) * out_h2
    d_w9 = d_o * out_o * (1 - out_o) * out_h3
    '''计算误差对参数w1,w2的偏导数'''
    '''d_w1=(y-y')*y*(1-y)*w_7*h_1*(1-h_1)*x_1'''
    d_w1=d_w7*w7*(1-out_h1)*x1
    d_w2 =d_w7*w7*(1-out_h1)*x2
    '''计算误差对参数w3,w4的偏导数'''
    '''d_w3=(y-y')*y*(1-y)*w_8*h_2*(1-h_2)*x_1'''
    d_w3 = d_w8 * w8 * (1 - out_h2) * x1
    d_w4 = d_w8 * w8 * (1 - out_h2) * x2
    '''计算误差对参数w5,w6的偏导数'''
    '''d_w5=(y-y')*y*(1-y)*w_9*h_3*(1-h_3)*x_1'''
    d_w5 = d_w9 * w9* (1 - out_h3) * x1
    d_w6= d_w9 * w9 * (1 - out_h3) * x2
    '''print("反向传播：误差传给每个权值")
    print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
          round(d_w7, 5), round(d_w8, 5),round(d_w9, 5))'''
    '''更新参数w4'''
    '''d_b4=(y-y')*y*(1-y)*1'''
    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8,d_w9


def update_w(w1, w2, w3, w4, w5, w6, w7, w8,w9,lr=1):
    # 步长
    step =lr
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    w9 = w9 - step * d_w9
    return w1, w2, w3, w4, w5, w6, w7, w8,w9


if __name__ == "__main__":
    w1, w2, w3, w4, w5, w6, w7, w8 ,w9= 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8 ,0.1
    b1,b2 ,b3,b4=0.1,0.21,0.11,0.22
    x1, x2 = 0.5, 0.3
    y=0.09
    print("=====输入值：x1, x2；真实输出值：y=====")
    print(x1, x2,y)
    print("=====更新前的权值=====")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2),round(w9, 2))

    for i in range(1000):

        out_o, out_h1, out_h2,out_h3 = forward_propagate(x1, x2)
        d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8,d_w9 = back_propagate(out_o,  out_h1, out_h2,out_h3)
        w1, w2, w3, w4, w5, w6, w7, w8 ,w9= update_w(w1, w2, w3, w4, w5, w6, w7, w8,w9)
        if i%100==0:
            print("=====第" + str(i) + "轮=====")
            print("损失函数：均方误差")
            error = (1 / 2) * (out_o - y) ** 2
            print(round(error, 5))
            print("反向传播：误差传给每个权值")
            print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
                  round(d_w7, 5), round(d_w8, 5), round(d_w9, 5))

    print("更新后的权值")
    print(round(w1, 2), round(w2, 2), round(w3, 2), round(w4, 2), round(w5, 2), round(w6, 2), round(w7, 2),
          round(w8, 2),round(w9, 2))

运行结果：
=====输入值：x1, x2；真实输出值：y=====
0.5 0.3 0.09
=====更新前的权值=====
0.2 -0.4 0.5 0.6 0.1 -0.5 -0.3 0.8 0.1
=====第0轮=====
损失函数：均方误差
0.15923
反向传播：误差传给每个权值
-0.00478 -0.00287 0.01154 0.00692 0.0016 0.00096 0.06637 0.08357 0.06414
=====第100轮=====
损失函数：均方误差
0.00058
反向传播：误差传给每个权值
-0.00076 -0.00046 -0.00036 -0.00022 -0.00056 -0.00033 0.0021 0.00241 0.00196
=====第200轮=====
损失函数：均方误差
6e-05
反向传播：误差传给每个权值
-0.00022 -0.00013 -0.00011 -7e-05 -0.00017 -0.0001 0.00058 0.00066 0.00054
=====第300轮=====
损失函数：均方误差
1e-05
反向传播：误差传给每个权值
-8e-05 -5e-05 -4e-05 -3e-05 -6e-05 -4e-05 0.00022 0.00025 0.0002
=====第400轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-4e-05 -2e-05 -2e-05 -1e-05 -3e-05 -2e-05 9e-05 0.0001 9e-05
=====第500轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-2e-05 -1e-05 -1e-05 -0.0 -1e-05 -1e-05 4e-05 5e-05 4e-05
=====第600轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-1e-05 -0.0 -0.0 -0.0 -1e-05 -0.0 2e-05 2e-05 2e-05
=====第700轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-0.0 -0.0 -0.0 -0.0 -0.0 -0.0 1e-05 1e-05 1e-05
=====第800轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第900轮=====
损失函数：均方误差
0.0
反向传播：误差传给每个权值
-0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
更新后的权值
0.57 -0.18 0.54 0.62 0.32 -0.37 -1.86 -1.07 -1.38

Process finished with exit code 0
 

pytorch实现：

import torch

def sigmoid(z):
    a = 1 / (1 + torch.exp(-z))
    return a

def forward_propagate(x1, x2):
    '''传入输入和参数'''
    '''隐藏层'''
    in_h1 = w1 * x1 + w2 * x2+b1
    out_h1 = sigmoid(in_h1)
    in_h2 = w3 * x1 + w4 * x2+b2
    out_h2 = sigmoid(in_h2)
    in_h3 = w5 * x1 + w6 * x2 + b3
    out_h3 = sigmoid(in_h3)
    '''输出层'''
    in_o =w7*out_h1+ w8 * out_h2 + w9 * out_h3+b4
    out_o = sigmoid(in_o)
    '''输出隐藏层输出和输出层输出'''
    return out_o


def loss_fuction(x1, x2, y):  # 损失函数
    y_pre = forward_propagate(x1, x2)  # 前向传播
    loss = (1 / 2) * (y_pre - y) ** 2  # 考虑 ： t.nn.MSELoss()

    return loss


def update_w(w1, w2, w3, w4, w5, w6, w7, w8,w9,lr=1):
    # 步长
    step =lr
    w1.data = w1.data - step * w1.grad.data
    w2.data = w2.data - step * w2.grad.data
    w3.data = w3.data - step * w3.grad.data
    w4.data = w4.data - step * w4.grad.data
    w5.data = w5.data - step * w5.grad.data
    w6.data = w6.data - step * w6.grad.data
    w7.data = w7.data - step * w7.grad.data
    w8.data = w8.data - step * w8.grad.data
    w9.data = w9.data - step * w9.grad.data
    w1.grad.data.zero_()  # 注意：将w中所有梯度清零
    w2.grad.data.zero_()
    w3.grad.data.zero_()
    w4.grad.data.zero_()
    w5.grad.data.zero_()
    w6.grad.data.zero_()
    w7.grad.data.zero_()
    w8.grad.data.zero_()
    w9.grad.data.zero_()
    return w1, w2, w3, w4, w5, w6, w7, w8,w9


if __name__ == "__main__":
    x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
    y = torch.Tensor([0.09])
    print("=====输入值：x1, x2；真实输出值：y1, y2=====")
    print(x1, x2, y)
    w1, w2, w3, w4, w5, w6, w7, w8, w9 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
        [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8]), torch.Tensor(
        [0.1])  # 权重初始值
    b1, b2, b3, b4 =torch.Tensor([0.1]),torch.Tensor([0.21]),torch.Tensor([0.11]),torch.Tensor([0.22])
    w1.requires_grad = True
    w2.requires_grad = True
    w3.requires_grad = True
    w4.requires_grad = True
    w5.requires_grad = True
    w6.requires_grad = True
    w7.requires_grad = True
    w8.requires_grad = True
    w9.requires_grad = True

    print("=====更新前的权值=====")
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)

    for i in range(1000):
        L = loss_fuction(x1, x2, y)  # 前向传播，求 Loss，构建计算图
        L.backward()  # 自动求梯度，不需要人工编程实现。反向传播，求出计算图中所有梯度存入w中
        if i%100==0:
            print("=====第" + str(i) + "轮=====")
            print("损失函数（均方误差）：", L.item())
            print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
                  round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
                  round(w8.grad.item(), 2),round(w9.grad.item(), 2))
        w1, w2, w3, w4, w5, w6, w7, w8,w9 = update_w(w1, w2, w3, w4, w5, w6, w7, w8,w9)

    print("更新后的权值")
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data,w9.data)

运行结果：
=====输入值：x1, x2；真实输出值：y1, y2=====
tensor([0.5000]) tensor([0.3000]) tensor([-0.0900])
=====更新前的权值=====
tensor([0.2000]) tensor([-0.4000]) tensor([0.5000]) tensor([0.6000]) tensor([0.1000]) tensor([-0.5000]) tensor([-0.3000]) tensor([0.8000])
=====第0轮=====
损失函数（均方误差）： 0.2770015299320221
    grad W:  -0.01 -0.0 0.02 0.01 0.0 0.0 0.09 0.11 0.08
=====第100轮=====
损失函数（均方误差）： 0.010019990615546703
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第200轮=====
损失函数（均方误差）： 0.00698486203327775
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第300轮=====
损失函数（均方误差）： 0.006001585628837347
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第400轮=====
损失函数（均方误差）： 0.005511465482413769
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第500轮=====
损失函数（均方误差）： 0.005217039026319981
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第600轮=====
损失函数（均方误差）： 0.005020393058657646
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第700轮=====
损失函数（均方误差）： 0.004879706539213657
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第800轮=====
损失函数（均方误差）： 0.004774070344865322
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
=====第900轮=====
损失函数（均方误差）： 0.004691848997026682
    grad W:  -0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0.0 0.0 0.0
更新后的权值
tensor([1.1253]) tensor([0.1552]) tensor([0.8931]) tensor([0.8359]) tensor([0.7716]) tensor([-0.0970]) tensor([-3.0736]) tensor([-2.3972]) tensor([-2.4912])

Process finished with exit code 0

总结：

分别用numpy和pytorch实现了误差逆传播的神经网络，对torch自动求导机制有了一定的了解。

用pytorch自动计算梯度显然是跟简单的方法，因为我们不需要自行推导损失函数对参数的偏导，大大省略了推导过程。

其他的考虑：

关于反向传播是否更新偏置b的探索 2.0_真不想再学了的博客-CSDN博客