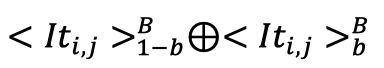双方比较
之前已经介绍过了利用加密电路或者比特分解来实现安全多方比较。本次再介绍一种利用不经意传输来实现双方比较的方法。
不经意传输在之前的科普进行过介绍,该比较协议的主要思路为:将需要比较的两个比特串分为多个部分,每个部分再进行比较,最后利用树形结构进行组合。假设有比特串和比特串,将比特串划分为两个部分,分别为\( _1,_0 \),将比特串也划分为\( _1 \)和\( _0 \)。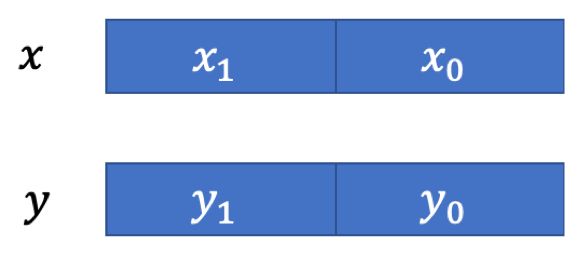
表达式1{<} 表示若<,则表达式1{<} 的值为1,否则为0。同理,表达式1{= } 表示若=则表达式的值为1,反之为0。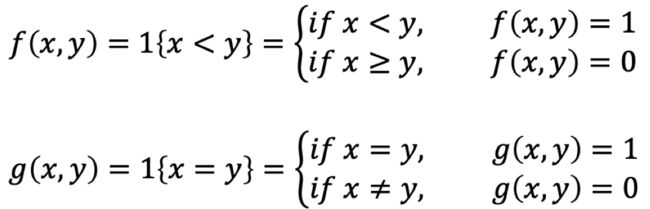
思考如下的比较:
$$ \begin{array}{c} x=x_{1} \| x_{0} \\ y=y_{1} \| y_{0} \\ 1\{x 把比特串和比特串分为两部分后,先比较\( _1和_1 \)的大小,由于\( _1和_1 \)都是高位部分,因此若\( _1<_1 \)则比特串<;反之若\( _1>_1 \)则>,在这两种情况下无需在比较\( _0,_0 \)的大小了。只有当\( _1=_1 \)时,需要通过比较\( _0,_0 \)的大小关系来确定, 的大小关系。 式1就是该比较协议的核心思想。该协议的详细流程为: 首先假设Alice掌握比特串,Bob掌握比特串,先考虑最简单的情况,和等长均为比特且\( \frac{l}{m} \)为2的指数倍。 1. Alice和Bob分别对和进行等分:Alice:把进行等分,每份比特: $$ x=x_{q-1}\|\cdots\| x_{0} $$ Bob:把进行等分,每份比特: $$ y=y_{q-1}\|\cdots\| y_{0} $$ 2. Alice产生两个随机数,将其分别记为\( { 即对于\( x_j \),Alice将比特\( s_{j,0}...s_{j,M-1} \)中下标为\( s_{j,0}...s_{j,x_j-1} \)的全都设置为随机数 \( { 即下标比\( x_j \)的值小的为随机数\( { 若用黄色表示比特值为1,蓝色表示比特值为0,则Alice在完成上述步骤后,\( s_{j,0}...s_{q-1,M-1} \)和\( t_{j,0}...t_{j,M-1} \)如下所示: 对于0≤≤−1,Alice对每个\( x_j \)都进行上述的步骤,因此能得到\( s_{0,0}...s_{j,M-1} \)共∙比特,得到\( t_{0,0}...t_{q-1,M-1} \)共∙比特。 3. Alice和Bob间调用次选1的OT协议,Alice在 OT 协议中的输入为\( s_{j,0}...s_{j,M-1} \),Bob在OT中的输入为\( y_i \): 次选1的OT结束后,Bob会获得\( s_{0,y_0}...s_{q-1,y_{q-1}} \)。 Alice和Bob再调用次选1的OT协议,Alice在OT协议中的输入为\( t_{j,0}...t_{j,M-1} \),Bob在OT中的输入为\( y_i \): 将\( s_{0,y_0}...s_{q-1,y_{q-1}} \)记为\( { Alice的输入为 \( s_{j,0}...s_{j,M-1} \),Bob的输入为\( y_i \),那么当\( y_i≥x_i \)时,Bob通过OT获得的为 \( { 同理可将Alice的输入为\( t_{j,0}...t_{j,M-1} \),Bob的输入为\( y_i \),OT后Bob获得的\( { 4. Alice和Bob运行如下算法(Alice运行则=0,Bob 运行则=1): 该算法的目的为将需要比较的比特串分成多个部分,每个部分进行比较, 再将比较结果进行组合。举个例子来解释这个算法,假设=16,则\( x=x_{15} | ... | x_{0} ,y=y_{15} | ... | y_{0}\),要比较和先比较\( x_{15} | ... | x_{8} \)和\( y_{15} | ... | y_{8} \)的大小,只有当\( x_{15} | ... | x_{8} \)和\( y_{15} | ... | y_{8} \)相等时才需要接着去比较\( x_{7} | ... | x_{0} \)和\( y_{7} | ... | y_{0} \)间的大小关系。而比较\( x_{15} | ... | x_{8} \)和\( y_{15} | ... | y_{8} \)间的大小关系可以先比较\( x_{15} | ... | x_{12} \)和\( y_{15} | ... | y_{12} 间的大小关系,若二者相等再比较\( x_{11} | ... | x_{8} \)和\( y_{11} | ... | y_{8} \),以此类推,则形成了一个树形结构。 最后最先需要比较的为和间的大小关系。用: $$ x=x^{(i)}=\frac{x^{i}_q}{2^i}-1 \| ... \| {x_{0}}^i $$ 表示该树形结构,()表示位于第几层,如 \( F_{} \)是多方函数,需要Alice和Bob共同完成操作。如掌握\( a_0 \)和\( b_0 \),Bob掌握\( a_1 \)和\( b_1 \),二者都调用\( F_{} \)后,\( F_{} \)对Alice的输出为\( (a\wedge b)_0 \),对Bob的输出为\( (a\wedge b)_1 \),具体实现可以使用之前介绍过的Beaver Triple完成,因此:
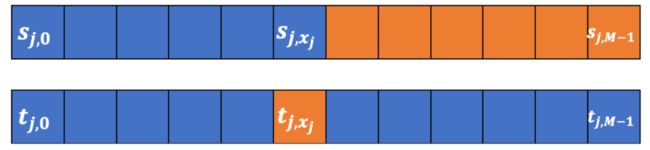


次选1的OT结束后,Bob会获得\( t_{0,y_0}...t_{q-1,y_{q-1}} \)。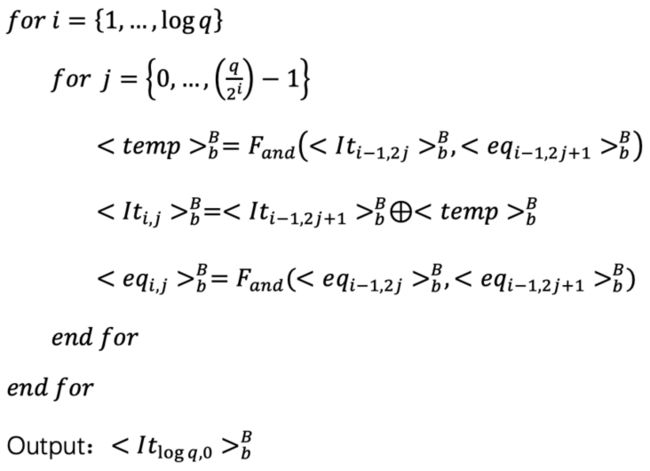
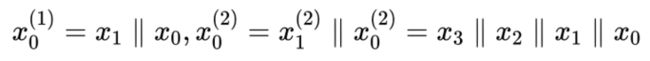
树形结构如下图所示: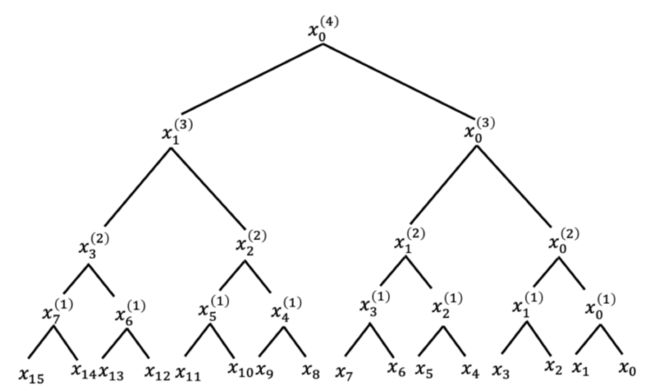
正确性证明: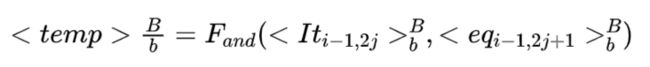
输出为:
则: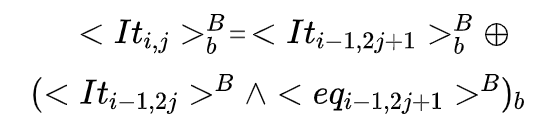
又由于: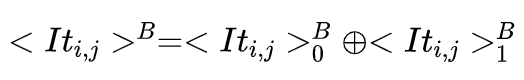
因此对\( {