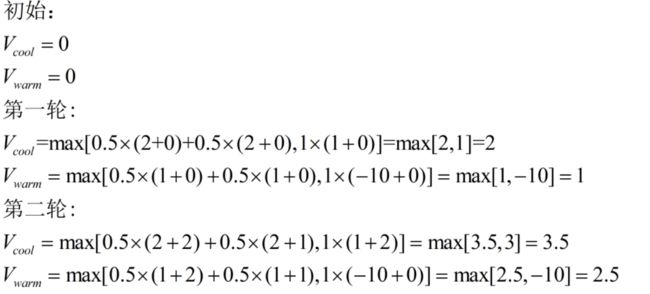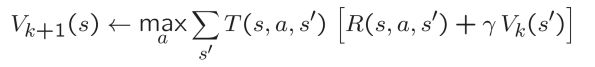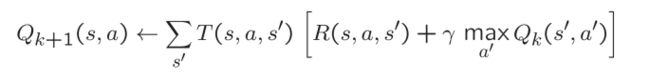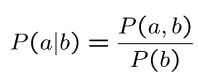UESTC人工智能 期末复习

目录

Part 0 AI历史

Part 1 图搜索算法

图搜索一般过程

深度优先搜索DFS

 广度优先搜素BFS

DFS和BFS的区别

一致代价搜索UCS

Greedy Search

⚠A* Search

Part 2 对抗搜索 Adversarial Search

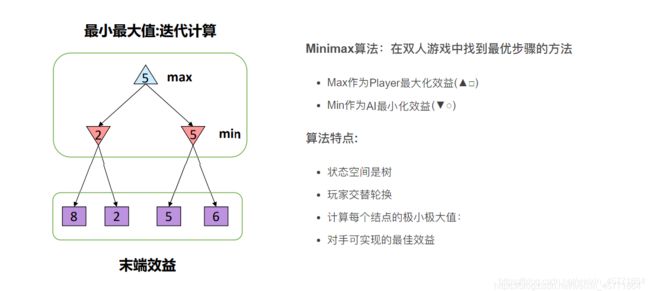
Minimax for Zero-Sum Games

估值函数evaluation function

⚠α β剪枝

Part3 MDP

价值迭代 Value Iteration

固定策略 Fixed Policies

策略提取 Policy Extraction

 策略迭代 Policy Iteration

 策略迭代和价值迭代的比较

⚠例 迷宫寻宝问题

Part 4 强化学习 Reinforcement Learning

Offline (MDPs) vs. Online (RL)

基于模型的学习 Model-Based Learning

 无模型学习 Model-Free Learning

直接评估 direct evaluation

时间差分学习 Temporal Difference Learning

主动强化学习 Active Reinforcement Learning

Q值迭代 Q-Value Iteration

 Q-Learning算法

Part 5 一阶逻辑

推理

命题

原子公式

连词和量词

等价关系

永真蕴含式

置换与合一

消解原理 resolution principle

鲁滨逊归结原理

Part 6 概率 probabiliity

概率公式

⚠例

Part 7 贝叶斯网络 bayes nets

概率判断独立性

⚠Active / Inactive Paths 判断独立性

 贝叶斯网络中的条件概率

 多重连接和多重消除 Multiple Joins & Multiple Elimination

 ⚠作业题

Part 8 机器学习 ML

监督学习  vs 无监督学习

回归 vs 分类 Regression vs Classification

训练集 vs 测试集 vs验证集

泛化和过拟合 Generalization & Overfitting

线性分类器 Linear Classifiers

激活函数 - 概率决策

⚠线性回归 

决策树 Decision Trees

决策树构建递归退出条件C

信息熵 Entropy

信息增益 Information Gain

⚠ID3算法实例

---

Part 0 AI历史

人工智能三大流派

• 行为学派：智能体、强化学习
• 符号学派：逻辑理论家、知识库系统
• 计算学派：神经网络、深度学习

1950年图灵提出 “ 计算机与智能” Computing Machinery and Intelligence

1956年达特茅斯会议提出 “人工智能”

Part 1 图搜索算法

图搜索一般过程

1. 建立一个只含有起始节点S的搜索图G，把S放到一个叫做OPEN 的未扩展节点表中
2. 建立一个叫做CLOSED的已扩展节点表，其初始为空表
3. LOOP：若OPEN表是空表，则失败退出
4. 选择OPEN表上的第一个节点,把它从OPEN表移出并放进CLOSED表中。称此节点为节点n
5. 若n为目标节点，则有解并成功退出，此解是追踪图G中沿着指针从n到S这条路径而得到的(指针将在第7步中设置)
6. 扩展节点n，同时生成不是n的祖先的那些后继节点的集合M。把M的这些成员作为n的后继节点添入图G中
7. n生成并记入M的子节点有以下三种情况：
   •  未曾在G中出现过的每个M成员：设置一个通向n的指针，并把它们加进OPEN表
   •  已经在OPEN表上的每一个M成员，确定是否需更改通到n的指针方向。
   •  已在CLOSED表上的每一个M成员：除需确定该子节点指向父节点的指针外，还需确定其后继节点指向父节点的指针(也就是，如该子节点的父节点根据需要(如代价值等)改变了，那就把该 子节点移回Open表)
8. 按某一任意方式或按某个探试值，重排OPEN表
9. GO LOOP

深度优先搜索DFS

完备性：否

最优解：否

 广度优先搜素BFS

 完备性：是

最优解：只有当每一步的cost都为1时才一定保证求得的解最优

DFS和BFS的区别

广度优先搜索(BFS)	深度优先搜索(DFS)
BFS在Graph中逐级访问节点。	DFS访问图深度明智的节点。 它会访问节点，直到到达叶或没有未访问节点的节点为止。
在开始任何其他节点之前，必须先充分探究一个节点。	一旦发现另一个未探索节点，就会暂停对该节点的探索。
使用队列数据结构存储未探索的节点。	使用堆栈数据结构存储未探索的节点。
BFS较慢，需要更多的内存。	DFS更快并且需要更少的内存。
一些应用： 在图中查找所有连接的组件。 查找两个节点之间的最短路径。 查找一个连接的组件内的所有节点。 测试图的二等性。	一些应用： 拓扑排序。 查找连接的组件。 解决迷宫等难题。 查找牢固连接的组件。 查找图形的关节点(切顶点)。

一致代价搜索UCS

一致代价搜索是在BFS上进行扩展的，也被成为代价一致搜索，他的基本原理是：一致代价搜索总是扩展路径消耗最小的节点N。N点的路径消耗等于前一节点N-1的路径消耗加上N-1到N节点的路径消耗。

 完备性：是

最优解：是

Greedy Search

每次选择到目前节点cost估值最小的子节点

由于估计值的选择问题，搜索结果不一定最优

完备性：否

最优解：否

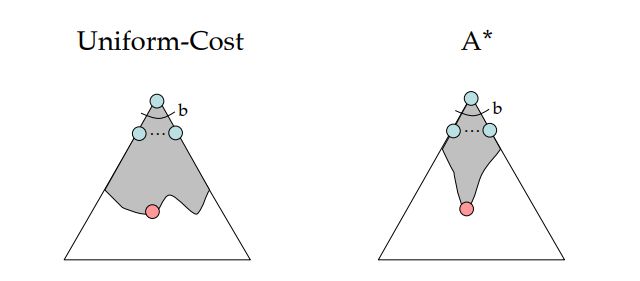
⚠A* Search

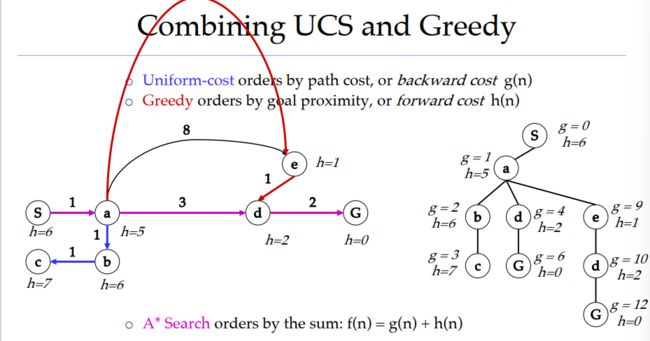
A*是UCS和Greedy的结合体

估值函数：f(n)=g(n)+h(n)

其中g(n)表示从起始搜索点到当前点的代价，需大于0；h(n)表示当前节点到目标节点的估值，需小于等于实际代价

 使用OPEN表和CLOSED表进行搜索

启发式搜索

启发式搜索是指利用当前与问题有关的信息作为启发式信息，这些信息是能够提升查找效率以及减少查找次数的。包括Greedy和A*搜索

Part 2 对抗搜索 Adversarial Search

零和游戏 Zero-Sum Games：

智能体之间具有对立的value，一个最大化value一个最小化value，对抗性的纯竞争

一般游戏 General Games：

智能体之间有独立的value，智能体竞争、合作或者互不影响都有可能

Minimax for Zero-Sum Games

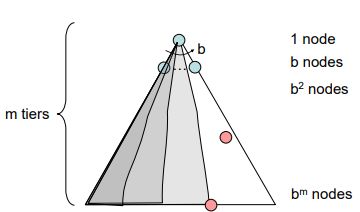
Game tree 的大小主要由两个数字决定：

1. 分支因子b： 代表了游戏典型的每步走棋的可行(合法)走法
2. 特征深度m： 游戏典型的走棋步数/深度

很容易得出，一个游戏的 Game tree 的大小，约为 b^m

估值函数evaluation function

目的：减小特征深度m

我们构造一个所谓的估值函数（evaluation function），它的目的是估计某个局面的 Minimax 评分，这样我们我们就不用搜索到终盘才能得知结果。一般而言，越接近终盘估计会越准确（因为游戏往往越到残局越简单），所以估值函数不能完全替代搜索

⚠α β剪枝

目的：减小分支因子b

 参考链接 ：

CS 161 Recitation Notes - Minimax with Alpha Beta Pruning (ucla.edu)

怎样做一道阿尔法贝塔剪枝的题(图解)_Sacredness的博客-CSDN博客_阿尔法贝塔剪枝

局限性：在现实游戏中，无法搜索到叶子节点

解决方案：限制搜索深度

Part3 MDP

MDP是一个五元组——状态空间、行为、状态转移概率、奖励、折扣因子

价值迭代 Value Iteration

对于采取某一动作Q值的计算，一般可以理解为：采取某一动作的reward+下一状态的V值，如果可能进入多个状态，那么就按照概率加权

例一：

值迭代缺点：

• 速度慢——每次迭代时间复杂度 O(S2A)
• 每个状态的“最大值”很少改变
• policy通常早在values之前收敛

固定策略 Fixed Policies

固定每一步的action由函数π(s)得到，那么V值计算如下，其实和价值迭代没太大区别

策略提取 Policy Extraction

在知道每一步的最优价值V*(s)时，还需要进行一个arg max()操作来求得执行哪个action会得到此最优价值

 

 策略迭代 Policy Iteration

包括两部分：

 策略评估：对于固定策略π ，通过策略评估得到V值，迭代直至v值收敛

策略提升：对于固定策略的V值，使用策略提取获得更好的策略：

局限：在不知道T和R时无法更新V

idea：对结果 s'（通过做动作！）和平均值进行采样

 策略迭代和价值迭代的比较

两者本质上都是计算最优value，都是用于解决MDP的动态程序

价值迭代：

• 每次迭代都更新value和policy
• 不跟踪policy，但在选择最大Q值时会隐式的重新计算他

策略迭代：

• 使用固定策略进行了几次更新实用程序的传递（每次传递都很快，因为我们只考虑一个动作，而不是所有动作）
• After the policy is evaluated, a new policy is chosen（慢如值迭代传递）
• 新policy会更优

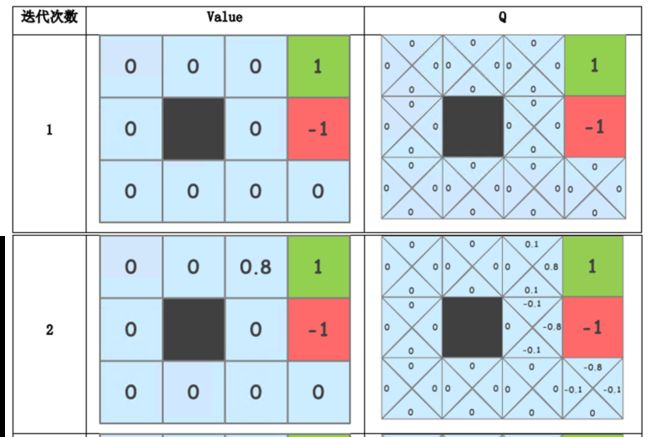
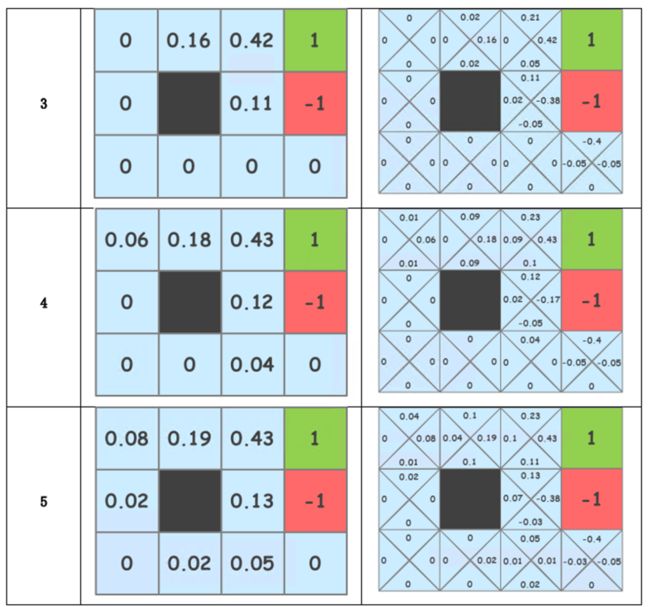
⚠例 迷宫寻宝问题

生存奖励为0代表每一步的R为0 

先计算Q表，再算V表，从非0的位置扩散

gamma=1

2 - 右上角：

上移Q=0.8×0+0.1×0+0.1×1=0.1

下移Q=0.8×0+0.1×0+0.1×1=0.1

左移Q=0.8×0+0.1×0+0.1×0=0

右移Q=0.8×1+0.8×0+0.8×0=0.8

 gamma=0.5

上移Q=0.5×0.8×0+0.5×0.1×0+0.5×0.1×1=0.05

下移Q=0.5×0.8×0+0.5×0.1×0+0.5×0.1×1=0.05

左移Q=0.5×0.8×0+0.5×0.1×0+0.5×0.1×0=0

右移Q=0.5×0.8×1+0.5×0.8×0+0.5×0.8×0=0.4

Part 4 强化学习 Reinforcement Learning

Offline (MDPs) vs. Online (RL)

基于模型的学习 Model-Based Learning

step1.通过training过程，计算状态转移矩阵T（）和动作reward R（），通过学习得到经验MDP模型

step2. 使用价值迭代或策略迭代求解最优values

 无模型学习 Model-Free Learning

学习者无法选择采取什么行动，跟着给的固定策略π走，执行策略并学习经验

Simplified task: policy evaluation

• Input: a fixed policy π(s)
• You don’t know the transitions T(s,a,s’)
• You don’t know the rewards R(s,a,s’)
• Goal: learn the state values

直接评估 direct evaluation

目标：计算在策略π下每个状态的value

实现：按照π采取行动，对于某个state，记下每个Episode中从他开始到结束的折扣奖励的总和，最后平均这些sample

计算过程：

A = [-10] / 1 =10

B = [(-1-1+10)+(-1-1+10)]/2 = +8

C = [(-1+10)+(-1+10)+(-1+10)+(-1-10)]/4 = +4

D = [10+10+10]/3 = +10

E = [(-1-1+10)+(-1-1-10)]/2 = -2

优点：简单易理解；不需要计算T、R；最终你那个计算出正确的平均value

缺点：浪费了状态连接的信息，每个状态必须单独学习，会花费较长时间学习

时间差分学习 Temporal Difference Learning

Big idea: learn from every experience!

 每经历一个转换（s, a, s', r）时更新 V(s)

 可能的结果将更频繁地提供更新

policy依然固定，仍然在进行策略评估

计算过程：

主动强化学习 Active Reinforcement Learning

照样不知道T，R，但是现在可以让智能体自己做出选择！

基本权衡：探索与开发，是选择基于已有经验选择老路还是进行随机贪婪探索选择新路？

Q值迭代 Q-Value Iteration

对比value迭代，初始化V0(S)=0

Q_value迭代初始化Q0(s,a)=0

 Q-Learning算法

基于Q-value迭代，类似于时间差分学习

其中maxQ(s',a'）是在下一状态 s' 的最大Q值

Part 5 一阶逻辑

推理

定义：推理就是按照某种策略从已知事实和知识推出结论的过程。

按推理的逻辑基础分类：

演绎推理：从一般到个别 ，三段论法（大前提、小前提、结论）

归纳推理：从个别到一般，从大量特殊实例出发，归纳出一般性结论

按所用知识的确定性分类：

确定性推理：所用的知识和证据都是确定的，要么为真要么为假，没有第三种情况

不确定性推理：不确定的

按推理中所用知识是否具有启发性分类：

启发式推理：效率高

非启发式推理：效率低

命题

命题的定义： 

• 断言：一个陈述句称为一个断言(assertion)
• 命题(proposition)：具有真假意义的断言

命题的真值：

• T：命题的意义为真
• F：命题的意义为假 

命题真值的说明

• 一个命题不能同时既为真又为假
• 一个命题可在一定条件下为真，而在另一条件下为假

原子公式

定义：由谓词符号和若干项组成的谓词演算。项包括: 常量符号、变量符号、函数符号等。

定义原子公式为真值或假值就表示了某种语义(semantics)。

若t1 , t2 , …, tn是项，P是谓词，则称P(t1 ,t2 ,…,tn )为原子谓词公式（原子公式）。

无变量的原子公式取值确定，包含变量的原子公式取值不定。

例如：“机器人（ROBOT）在1号房间（room1）内”

         INROOM（ROBOT，room1） 为真

         INROOM（ROBOT，room2）为假

连词和量词

1. 与、合取（conjunction)：用连词∧把几个公式连接起来而构成的公式。

   合取项是合取式的每个组成部分。

   例：LIKE(I，MUSIC)∧LIKE(I，PAINTING) （我喜爱音乐和绘画。）

2. 或、析取（disjunction）：用连词∨把几个公式连接起来而构成的公式。

   析取项是析取式的每个组成部 

   例：PLAYS(LILI，BASKETBALL)∨PLAYS(LILI，FOOTBALL) （李力打篮球或踢足球。）

3. 蕴涵（Implication）:“→”表示“如果—那么”（IF—THEN）关系，其所构成 的公式叫做蕴涵。

4. 非（Not）表示否定，¬、～均可表示

连词的优先级 ： ¬, ∧, ∨, , →, ↔

 合式公式的真值表

等价关系

等价(Equivalence): 如果两个合式公式，无论如何解释，其真值表都 是相同的，那么我们就称此两合式公式是等价的。

 

永真蕴含式

置换与合一

置换定义：置换是形如{t1 /x1 ,t2 /x2 ,…,tn /xn }的有限集合，其中t1 ,t2 ,…,tn是项；x1 ,x2 ,…,xn 是互不相同的变元；ti /xi 表示用项ti 替换变元xi 。

要求：ti与xi 不能相同，xi 不能循环地出现在另一个ti 中。

例如：{a/x, c/y, f(b)/z} 是一个置换， 但 {g(z)/x, f(x)/z}不是一个置换，原因是x和z之间出现了循环置换现象，若改为{g(a)/x, f(x)/z}即可

设θ={t1 /x1 ,t2 /x2 ,…,tn /xn }是一个置换，F是一个谓词公式， 把公式F中出现的所有xi 换成ti(i=1,2,…,n)，得到一个新的公式G， 称G为F在置换θ 下的例示，记作G=Fθ

置换的合成（了解）

 合一定义：设有公式集F={F1 , F2 ,…,Fn }，若存在一个置换θ，可使 F1θ=F2θ=…=Fnθ， 则称θ是F的一个合一。称F1 ,F2 ,…,Fn是可合一的。

例：

设有公式集F={P(x, y, f(y)), P(a, g(x), z)}，则 λ={a/x, g(a)/y, f(g(a))/z} 是它的一个合一。

一般情况下,一个公式集的合一不惟一。

最一般合一：设σ是谓词公式集F的一个合一，如果对F的任意一个合一θ都存在一个置换λ，使得 θ= σ· λ，则称σ是一个最一 般(或最简单)合一

消解原理 resolution principle

定义：对谓词演算公式进行分解、化简，消去一些符号, 以求得导出子句，又称归结。

消解过程：消解规则应用于母体子句对, 以便产生导出子句

鲁滨逊归结原理

核心：两个子句的归结式、

定义1：若P是原子谓词公式，则称P与﹁P为互补文字

定义2：设C1和C2是子句集中的任意两个子句，如果C1中的文字L1与C2中的文字L2互补，那么可从C1和C2中分别消去L1和L2，并将C1和C2中余下的部分按析取关系构成一个新的子句C12，则称这一过程为归结，称C12为C1和C2的归结式，称C1和C2为C12的亲本(父辈)子句

Part 6 概率 probabiliity

概率公式

链式条件概率：

例1：

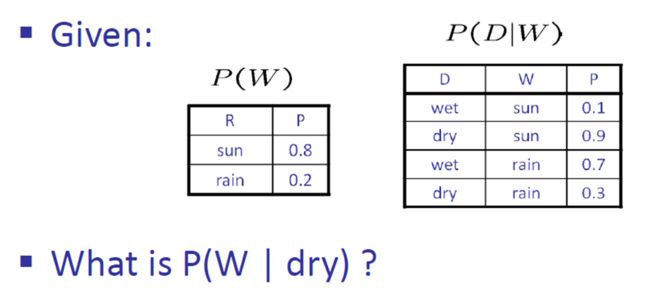
⚠例

 

 首先明确，P(W |  dry)是一个概率分布，而不是一个概率值。不能写成 P(W |  dry)=....

①求联合概率分布P(D,W);

②求边缘概率分布)P(D);

③求条件概率分布P(W | D).

P(W |  dry)
D	W	P
dry	sun	0.9231
dry	rain	0.0769

Part 7 贝叶斯网络 bayes nets

概率判断独立性

判断独立性的重要公式：

条件独立性：

⚠Active / Inactive Paths 判断独立性

要判断X，Y的独立性：

1. 找到X到Y的所有路径paths

2. 如果一个path的所有三元组都是active那么此path就是active

3.若存在一个path为active，那么X、Y就是非独立的，反之独立

简言之：找到一条path的所有三元组都是active那么就非独立；

                若只存在一条路径，那么找到一个inactive的三元组就独立，如果全部active才非独立

可以把X、Y理解为两个水池，如果有一根连通水管（path）里的开关全打开了（active）那么二者连通，不独立（independence）；如果就只有一根水管连接，那么只要有一个开关被关闭（inactive）那么就独立。

只需要记间接因果和同因是active，其他三个对立的象限自己就出来了

25-bn (washington.edu)

 贝叶斯网络中的条件概率

 例：

 多重连接和多重消除 Multiple Joins & Multiple Elimination

 ⚠作业题

Part 8 机器学习 ML

监督学习  vs 无监督学习

监督学习：输入已知类别的数据样本         分类、回归

无监督学习：输入未知类别的数据样本      聚类

回归 vs 分类 Regression vs Classification

分类：对输入数据进行离散值标签的预测

回归：预测连续的、具体的数值

Output： 连续 vs 离散

分类需要激活函数

训练集 vs 测试集 vs验证集

训练集用于学习参数（例如模型概率）

测试集用于计算模型的准确率

验证集用于调节超参数

泛化和过拟合 Generalization & Overfitting

在有监督学习中，我们会在训练数据集上建立一个模型，之后会把这个模型用于新的，之前从未见过的数据中，这个过程称为模型的泛化

模型在训练集上表现好，在测试集验证集表现差就说明出现了过拟合问题，出现这种情况的主要原因是训练数据中存在噪音或者训练数据太少

解决办法：选取合适的停止训练标准；使用验证数据集；获取额外数据进行交叉验证；正则化

Relative frequency parameters will overfit the training data

相对频率参数会过拟合训练数据

线性分类器 Linear Classifiers

输入特征向量 f(x) 

权重 向量  w

在二分类中：

真实标签为 y*∈{-1，1}，

预测标签为 y ，w和f(x)在同一平面则为正样本，y=1

如果分类正确，不更新w，分类错误则更新 w

w = w + y* · f(x)   其中y* = 1或-1

 在多分类中：

输入特征向量 f(x) 

每个类别的权重 向量 

 预测标签为 y ，取最大的一个类别标签

 如果分类正确，不更新w；分类错误则更新 w，此时需要分别对正确和错误的两个w进行更新

关键点：减小错分类别的向量点积，增大真实类别的向量点积

          

激活函数 - 概率决策

 

⚠线性回归 

 L2 loss：所有样本的平方误差和

internati

例：

 

 

决策树 Decision Trees

决策树构建递归退出条件C

• 当前样本集D包含的样本属于同一类别C
• 当前属性集A为空或样本集D中所有样本在所有属性上取值相同（但类别可能不相同）
• 当前结点包含的样本集为空

信息熵 Entropy

信息熵是度量样本集合纯度的指标

假定当前样本集合D中第k类样本所占比例为pk（k=1，2，...，|y|）则D的信息熵的定义为：

 Ent(D)的取值范围为 [0,log2|y| ]，值越小，纯度越高

计算信息熵时约定：若p=0，则=0

信息增益 Information Gain

样本集D的某个离散属性a有V个可能的取值，用a来对D进行划分则会产生V个分支结点，其中第v个分支结点包含了D中所有在在属性a上取值为的样本，记为。定义用属性a对样本集D进行划分所获得的信息增益为：

 一般而言，信息增益越大，意味着使用属性a来进行划分获得的纯度提升越大

在ID3算法中选择信息增益大的属性来划分样本集

⚠ID3算法实例